Il primo grafico sopra mostra che i lotti più grandi percorrono effettivamente meno distanza per epoca. La distanza dell’epoca di addestramento del batch 32 varia da 0,15 a 0,4, mentre per l’addestramento del batch 256 è di circa 0,02-0,04. Infatti, come possiamo vedere nel secondo grafico, il rapporto delle distanze epocali aumenta nel tempo!
Ma perché l’addestramento a grandi lotti percorre meno distanza per epoca? È perché abbiamo meno lotti, e quindi meno aggiornamenti per epoca? O è perché ogni aggiornamento del batch percorre meno distanza? Oppure, la risposta è una combinazione di entrambi?
Per rispondere a questa domanda, misuriamo la dimensione di ogni aggiornamento batch.

Median batch update norm for batch size 32: 3.3e-3
Median batch update norm for batch size 256: 1.5e-3
Si può notare che ogni aggiornamento batch è più piccolo quando la dimensione batch è maggiore. Perché dovrebbe essere così?
Per capire questo comportamento, impostiamo uno scenario fittizio, dove abbiamo due vettori di gradiente a e b, ognuno dei quali rappresenta il gradiente per un esempio di allenamento. Pensiamo a come la dimensione media di aggiornamento del batch per batch size=1 si confronta con quella di batch size=2.

Se usiamo un batch size di uno, faremo un passo in direzione di a, poi b, finendo al punto rappresentato da a+b. (Tecnicamente, il gradiente per b verrebbe ricalcolato dopo l’applicazione di a, ma ignoriamolo per ora). Questo risulta in una dimensione media di aggiornamento del batch di (|a|+|b|)/2 – la somma delle dimensioni degli aggiornamenti del batch, divisa per il numero di aggiornamenti del batch.
Tuttavia, se usiamo una dimensione del batch di due, l’aggiornamento del batch è invece rappresentato dal vettore (a+b)/2 – la freccia rossa nella Figura 12. Quindi, la dimensione media di aggiornamento del batch è |(a+b)/2| / 1 = |a+b|/2.
Ora, confrontiamo le due dimensioni medie di aggiornamento del batch:

Nell’ultima riga, abbiamo usato la disuguaglianza del triangolo per mostrare che la dimensione media di aggiornamento del batch per la dimensione del batch 1 è sempre maggiore o uguale a quella del batch 2.
In un altro modo, affinché la dimensione media del batch per la dimensione del batch 1 e del batch 2 sia uguale, i vettori a e b devono essere rivolti nella stessa direzione, poiché questo è quando |a| + |b| = |a+b|. Possiamo estendere questo argomento a n vettori – solo quando tutti gli n vettori puntano nella stessa direzione, le dimensioni medie di aggiornamento dei lotti per batch size=1 e batch size=n sono uguali. Tuttavia, questo non è quasi mai il caso, poiché è improbabile che i vettori del gradiente puntino esattamente nella stessa direzione.

Se torniamo all’equazione di aggiornamento del minibatch nella figura 16, stiamo in un certo senso dicendo che quando aumentiamo la dimensione del lotto |B_k|, la grandezza della somma dei gradienti aumenta relativamente meno velocemente. Questo è dovuto al fatto che i vettori del gradiente puntano in direzioni diverse, e quindi raddoppiando la dimensione del lotto (cioè il numero di vettori del gradiente da sommare) non raddoppia la grandezza della somma risultante dei vettori del gradiente. Allo stesso tempo, stiamo dividendo per un denominatore |B_k| che è due volte più grande, risultando in un passo di aggiornamento complessivamente più piccolo.
Questo potrebbe spiegare perché gli aggiornamenti dei lotti per lotti più grandi tendono ad essere più piccoli – la somma dei vettori gradiente diventa più grande, ma non può compensare completamente il denominatore più grande|B_k|.
Ipotesi 2: L’addestramento per piccoli lotti trova minimizzatori più piatti
Misuriamo ora la nitidezza di entrambi i minimizzatori, e valutiamo l’affermazione che l’addestramento per piccoli lotti trova minimizzatori più piatti. (Si noti che questa seconda ipotesi può coesistere con la prima – non si escludono a vicenda). Per fare ciò, prendiamo in prestito due metodi da Keskar et al.
Nel primo, tracciamo la perdita di addestramento e di convalida lungo una linea tra un piccolo minimizzatore di batch (batch di dimensione 32) e un grande minimizzatore di batch (batch di dimensione 256). Questa linea è descritta dalla seguente equazione:

dove x_l* è il minimizzatore di grandi lotti e x_s* è il minimizzatore di piccoli lotti, e alpha è un coefficiente tra -1 e 2.

Nota che questo è un modo piuttosto semplicistico di misurare la nitidezza, poiché considera solo una direzione. Così, Keskar et al propongono una metrica di nitidezza che misura quanto la funzione di perdita varia in un quartiere intorno a un minimizzatore. In primo luogo, definiamo il quartiere come segue:

dove epsilon è un parametro che definisce la dimensione del vicinato e x è il minimizzatore (i pesi).
Poi, definiamo la metrica di nitidezza come la perdita massima in questo quartiere intorno al minimizzatore:

dove f è la funzione di perdita, con gli input che sono i pesi.
Con le definizioni di cui sopra, calcoliamo la nitidezza dei minimizzatori a varie dimensioni del lotto, con un valore di epsilon di 1e-3:
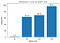
Questo mostra che i minimizzatori di lotti grandi sono effettivamente più nitidi, come abbiamo visto nel grafico di interpolazione.
Infine, proviamo a tracciare i minimizzatori con una visualizzazione di perdita normalizzata dal filtro, come formulato da Li et al . Questo tipo di grafico sceglie due direzioni casuali con le stesse dimensioni dei pesi del modello, e poi normalizza ogni filtro convoluzionale (o neurone, nel caso degli strati FC) per avere la stessa norma del filtro corrispondente nei pesi del modello. Questo assicura che la nitidezza di un minimizzatore non sia influenzata dalle grandezze dei suoi pesi. Poi, si traccia la perdita lungo queste due direzioni, con il centro del grafico che è il minimizzatore che vogliamo caratterizzare.