Un percentile è una posizione in una distribuzione che ha una specifica quantità (o percentuale) della distribuzione “sotto di essa” (alla sua sinistra). In altre parole, se il #n^”th “# percentile è #x#, e noi estraiamo un numero casuale #X# dalla distribuzione, allora la probabilità che #X# sia inferiore a #x# è #n %#:
#n^”th” “percentile” = x” “#means#” ” P(X < x)=n%.#
Per esempio, in una curva normale standard (con #mu = 0# e #sigma = 1#), il punto dove #x=0# (cioè l’asse #y#) è il 50° percentile, perché il 50% dell’area della curva cade a sinistra di #x=0#:

La distribuzione normale standard #Z# è una linea di base così buona che abbiamo una tabella di valori progettata appositamente per cercare i percentili per questa curva. Si chiama tabella #z# e assomiglia a questa:
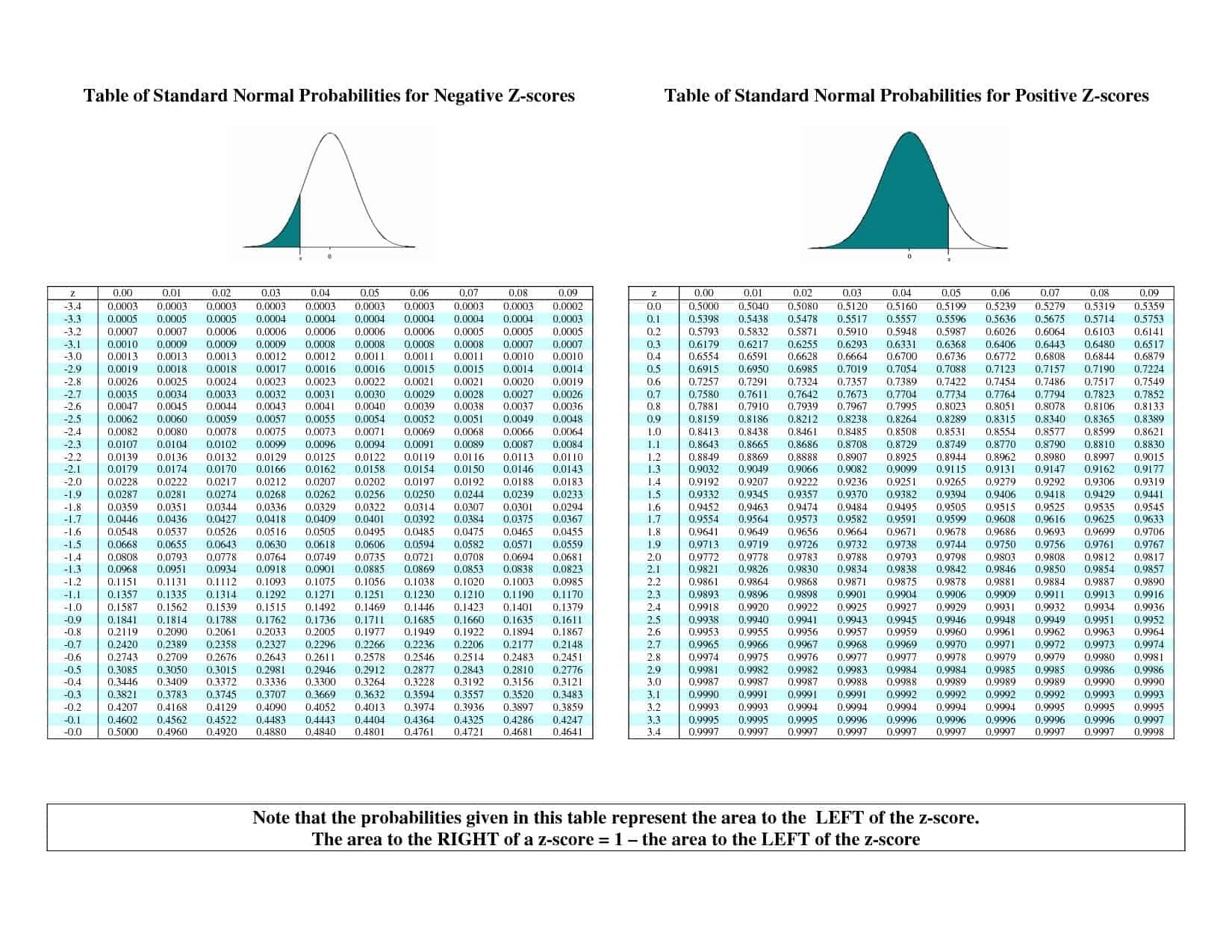
Come si usa? Diciamo che vogliamo il 25° percentile della distribuzione normale standard. Troviamo il valore più vicino a 0,25 nella tabella (che è 0,2514) e vediamo che è nella riga #”-“0,6# e nella colonna #0,07#. Per questa tabella, ciò significa che il 25° percentile è (approssimativamente) #”-“0.67#.
Ma aspetta, come ci aiuta questo quando vogliamo un percentile per qualsiasi distribuzione normale #X#? Dobbiamo trovare una connessione tra qualsiasi curva e la curva normale standard. Questa connessione si trova spostando la distribuzione #X# da sinistra a destra in modo che sia centrata a #0#, e poi allungandola/spazzandola in modo che la sua deviazione standard sia #1#. La formula per questo è:
#Z=(X-mu)/sigma#
dove #mu# è la media di #X# e #sigma# è la deviazione standard di #X#.
Se conosciamo il percentile che vogliamo dalla distribuzione #Z#, possiamo risolvere per #X# riorganizzando l’equazione in
#X=sigma Z + mu#.
Come esempio, usiamo la prima domanda che hai fatto, dove #X# è distribuito normalmente con #mu = 81.2# e #sigma = 12.4#, e cerchiamo il 16° percentile.
Dalla tabella sopra, il 16° percentile della distribuzione #Z# è circa #”-“0.99#. La posizione equivalente nella nostra distribuzione #X# è quindi:
#X=(12.4)(“-“0.99)+81.2#
#color(white)X=”-“12.276+81.2#
#color(white)X=68.924#
Quello che dice è: se #X# è una curva normale con #mu=81.2 ” piedi “# e #sigma = 12.4 ” piedi “#, allora c’è il 16% di possibilità che un’osservazione di #X# sia inferiore a #68,924 ” piedi “#.
Il resto te lo lascio come esercizio; con le formule di cui sopra, non dovrebbe essere così difficile.
Spero che questo aiuti!