Een percentiel is een plaats in een verdeling waar een bepaalde hoeveelheid (of percentage) van de verdeling “onder ligt” (links ervan). Met andere woorden, als het #n^”th “# percentiel #x# is, en we trekken een willekeurig getal #X# uit de verdeling, dan is de kans dat #X# kleiner is dan #x# #n %#:
#n^”th” ” percentiel” = x” “#means#” ” P(X < x)=n%.#
Bij voorbeeld, in een standaard normale curve (met #mu = 0# en #sigma = 1#), het punt waar #x=0# (d.w.z. de #y#-as) het 50ste percentiel, omdat 50% van het gebied van de kromme links van #x=0# valt:

De standaard normale verdeling #Z# is zo’n goede basislijn dat we eigenlijk een tabel met waarden hebben die speciaal ontworpen is om percentielen voor deze kromme op te zoeken. Dat heet een #z#-tabel, en die ziet er ongeveer zo uit:
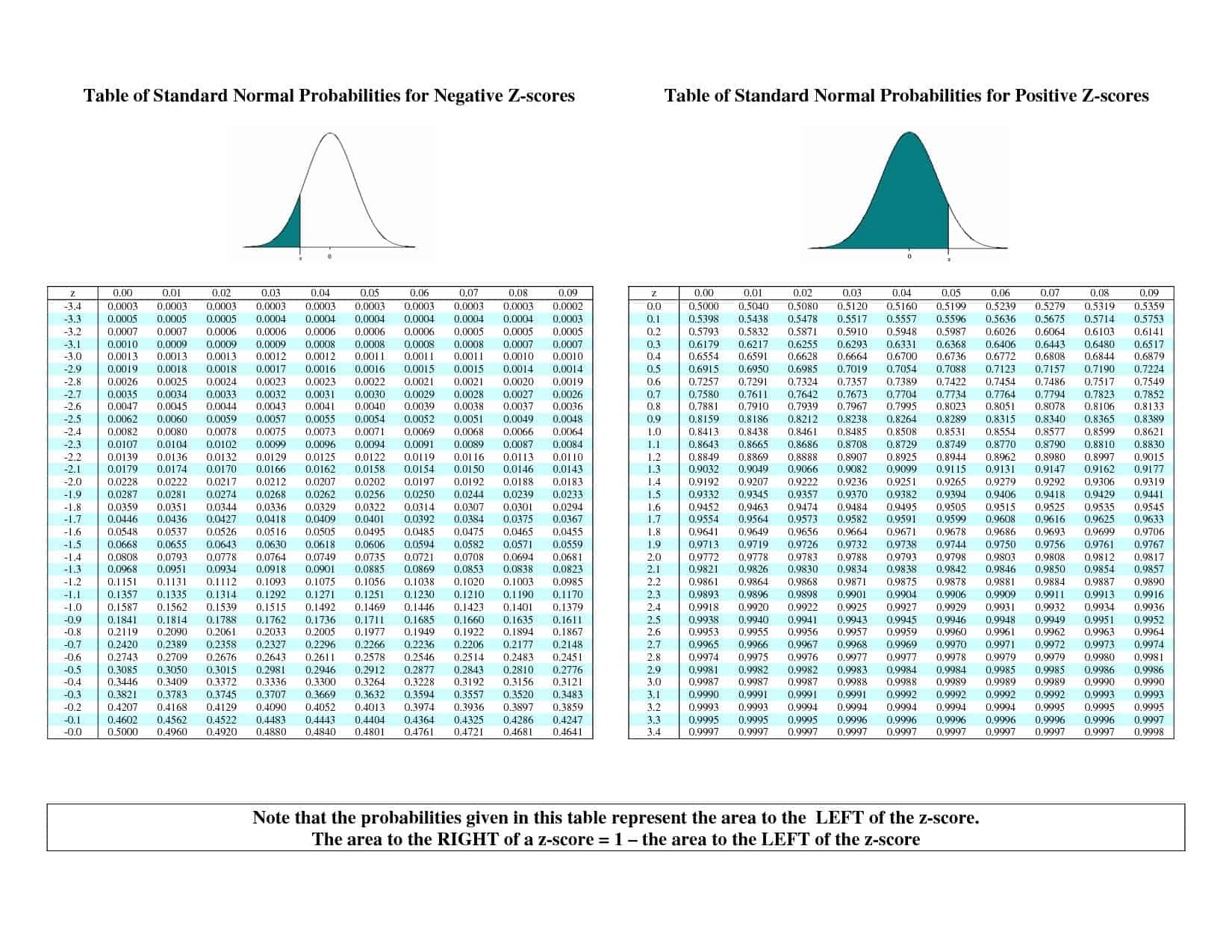
Hoe gebruiken we die? Laten we zeggen dat we het 25e percentiel willen voor de standaard normale verdeling. We zoeken de waarde die het dichtst bij 0,25 in de tabel ligt (en dat is toevallig 0,2514) en zien dat die in rij #”-“0,6# en kolom #0,07# staat. Voor deze tabel betekent dat dat het 25ste percentiel (ongeveer) #”-“0.67# is.
Maar wacht eens, hoe helpt dat als we een percentiel willen voor een willekeurige normale verdeling #X#? We moeten een verband vinden tussen een willekeurige kromme en de standaardnormale kromme. Dat verband wordt gevonden door de #X# verdeling van links naar rechts te verschuiven zodat ze gecentreerd is op #0#, en haar dan uit te rekken zodat haar standaardafwijking #1# is. De formule hiervoor is:
#Z=(X-mu)/sigma#
waarbij #mu# het gemiddelde van #X# is en #sigma# de s.d. van #X#.
Als we het gewenste percentiel van de #Z#-verdeling kennen, kunnen we #X# oplossen door de vergelijking te herschikken tot
#X=sigma Z + mu#.
Als voorbeeld gebruiken we de eerste vraag die u stelde, waarbij #X# normaal is verdeeld met #mu = 81,2# en #sigma = 12,4#, en we het 16e percentiel zoeken.
Uit de tabel hierboven blijkt dat het 16e percentiel van de #Z# verdeling ongeveer #”-“0,99# is. De overeenkomstige plaats in onze #X# verdeling is dan:
#X=(12,4)(“-“0,99)+81,2#
#color(white)X=”-“12,276+81.2#
#color(white)X=68.924#
Wat dit zegt is: als #X# een normale kromme is met #mu=81.2 ” voet “# en #sigma = 12.4 ” feet “#, dan is er 16% kans dat een waarneming van #X# kleiner is dan #68.924 ” feet “#.
De rest laat ik voor u als oefening; met de formules hierboven moet het niet zo moeilijk zijn.
Hoop dat dit helpt!