Een controlekaart is een mechanisme om inzicht te krijgen in procesgedrag, voorspelbaarheid en stabiliteit in de tijd. We weten dat elk proces een zekere mate van natuurlijke variabiliteit kent. Maar hoe weten we of de variabiliteit van het proces “uit de hand is gelopen”?
Een controlediagram is een hulpmiddel dat wordt gebruikt bij “kwaliteitscontrole” om te bepalen of er een ongeplande verandering in een proces heeft plaatsgevonden. Een proces continue variabele X meet dit. Voorbeeld procesvariabelen kunnen zijn, maar zijn niet beperkt tot, zoals –
- wachttijd in een fast-food restaurant of bij een incheckbalie op een vliegveld,
- schedule en kostenvariantie over iteraties,
- volume en frequentie van scope veranderingen over iteraties,
Wij ontwikkelen gewoonlijk Control Charts voor processen –
- die repetitief zijn voor het produceren van gefabriceerde partijen, en
- Verwachtingen zijn ingesteld om te presteren rond continue proces variabele X.
Een herhaalbaar proces is een proces waarin hetzelfde op dezelfde manier wordt gedaan en dezelfde resultaten oplevert.
Volgens de PMBOK® Guide is een controlediagram :-
Een visuele weergave van gegevens in de tijd en tegen vastgestelde controlegrenzen, die een middellijn heeft die helpt bij het detecteren van een trend van uitgezette waarden in de richting van een van beide controlegrenzen
Een controlediagram heeft de volgende componenten:
- Middellijn: De middellijn in het controlediagram wordt weergegeven als het gewenste ideale vermogen van een proces. Het is een grafische weergave van continue procesvariabele X . De middellijn is het berekende gemiddelde van de datapunten. Deze datapunten zijn repetitieve procesoutput in de tijd.
- Specificatielimiet: Wij stellen specificatielimieten vast, gewoonlijk na analyse van de verwachtingen van de klant. Soms vermelden wij deze grenzen in overeenkomsten. Er kunnen sancties aan verbonden zijn als de gegevenspunten aan specificatielimiet overschrijden.
- Controle Grenzen: We stellen boven- en ondergrenzen vast voor controlediagrammen. Wij ontwerpen deze grenzen gebruikend statistische analyse of van historische verslagen. Wij plotten gegevenspunten van een proces om tendensanalyse naar één van beide controlegrenzen en met betrekking tot de middellijn uit te voeren.
Voor herhaalde processen, worden de controlegrenzen over het algemeen geplaatst op +_ 3 sigma rond een proces. Variabele X of procesgemiddelde, d.w.z. hartlijn. De bovenste controlegrens wordt getrokken op 3 standaarddeviaties boven het procesgemiddelde, en de onderste op 3 standaarddeviaties onder de middellijn, of procesgemiddelde.
We stellen deze grenzen vast om te voorspellen of het proces corrigerende maatregelen nodig heeft om de procesprestaties in overeenstemming te brengen met de vereiste stabiliteit en capaciteit. Analyse van datapunten met de middellijn en controlegrenzen helpen ons om onnatuurlijke procesprestaties in de tijd te voorkomen. De controlegrenzen zijn strenger dan de specificatiegrenzen. Zodat we corrigerende maatregelen kunnen nemen voordat de datapunten in de buurt van de specificatielimiet komen.
Grafische weergave van componenten van de controlegrafiek: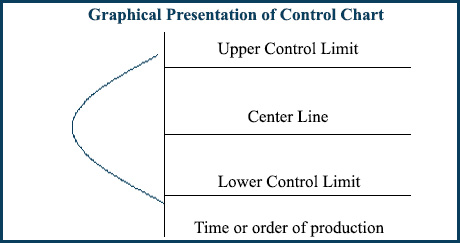
Hoe bepalen we of het proces “In Control” of “Out of Control” is? En dan analyseren we hoe we deze gegevens kunnen presenteren ten opzichte van de –
hartlijn en de &bovenste
onderste controlegrens. De nadruk ligt op het begrijpen of de gegevenspunten binnen aanvaardbare grenzen liggen.
Gegevenspunten binnen +- 3 sigma zijn “in Control”, en binnen aanvaardbare grenzen exclusief de regel van zeven (later beschreven). Datapunten binnen +-3 sigma betekent dat deze datapunten geen van beide controlelimieten overschrijden. Alles buiten de controlegrens vereist onderzoek.
Nu komen we bij de – Wat is regel van zeven in projectmanagement?
Wanneer zeven opeenvolgende datapunten aan weerszijden van het gemiddelde komen –
Dan nemen we dit proces Out of Control op basis van de heuristiek van Regel van Zeven.
In dit geval overschrijden de datapunten de controlegrenzen weliswaar niet, maar aangezien het herhaalde proces geen willekeurige output genereert –
Dit kan een signaal zijn van een probleem in een proces. Er worden inspanningen geleverd om de situatie en de oorzaak van het procesprobleem te begrijpen.
Kortom, het proces is niet onder controle.
- Wanneer de gegevenspunten buiten de bovenste of onderste controlegrenzen liggen en/of
- Zeven opeenvolgende punten worden uitgezet aan weerszijden van het gemiddelde, d.w.z. de middellijn.
We moeten beide speciale oorzaken van variantie onderzoeken.
Ontwikkeling van controlediagram:
Zoals ik al eerder zei, worden controlediagrammen gebruikt om te laten zien of een zich herhalend proces –
- “in control” of
- “out of control” is.
Ik neem een voorbeeld van een proces om repeterende wekelijkse builds te testen. Op een gemiddelde vrijdag EOD, moeten we de wekelijkse build afmaken. Nu moeten we het aanvaardbare bereik begrijpen. Uit waarnemingen blijkt dat we soms 1 of 2 dagen te laat zijn en soms een dag te vroeg.
De proceseigenaar kan accepteren dat een build een dag te laat of te vroeg is. Maar hoe kunnen we wiskundig zeggen dat –
- Een aanvaardbare variatie zou één dag of twee dagen zijn? En
- Als een week builds worden afgewerkt op een punt, waar de noodzaak voor corrigerende maatregelen wordt geïdentificeerd.
De controlegrafiek wordt gebruikt om wiskundige identificatie van controle grenzen en de noodzaak voor corrigerende maatregelen te begrijpen.
Voorstel dat we 30 weken van gegevens hebben verzameld om te begrijpen of proces output is binnen aanvaardbare grenzen.
Nu moeten we het gemiddelde van de slippage in builds voor 30 weken te berekenen: Gemiddelde vertraging van datapunten in dagen, d.w.z. 0,73 dagen.
Nu wordt de standaardafwijking berekend. Standaardafwijking betekent hoeveel afwijking van het gemiddelde: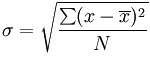
σ = de standaardafwijking
x = elke waarde in de populatie
x̄ = het gemiddelde van de waarden
N = het aantal waarden
Gebruik makend van bovenstaande formule zal de standaardafwijking 5,132273364 zijn.
Om controle grenzen te krijgen, moeten we de standaardafwijking vermenigvuldigen met 3. In dit geval zal de drie sigma waarde 15.39682009.
Nu is het tijd om de bovenste en onderste controle limiet te berekenen:
De bovenste controle limiet zal de som van 3 Sigma en gemiddelde slip in weken zijn, d.w.z. de som van 15.39682009 en 0,73. Het resultaat is 16,13 als bovenste controlegrens.
Lage controlegrens is 3 Sigma aftrekken van de gemiddelde afwijking in weken, d.w.z. 15,39682009 aftrekken van 0,73. Als resultaat krijgen we -14,66 als onderste controlegrens.
Samengevat:
Hier is 3 Sigma gelijk aan 15,39682009, het gemiddelde van de ontsporing in dagen is 0,73 dagen, de bovenste controlegrens is 16,13, en de onderste controlegrens is -14.66.
Nu kan eindelijk een controlegrafiek worden ontwikkeld met behulp van een 2D-lijngrafiekplot: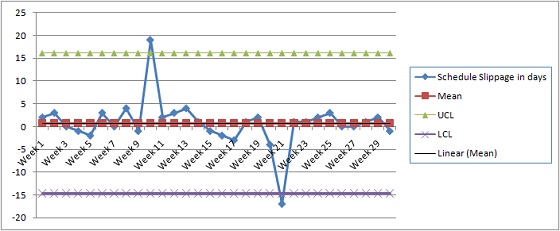
Controlegrafiek (x) met gebruikmaking van gemiddelde + 3 sigma en gemiddelde – 3 sigma controlegrenzen
Nu moeten we de grafieken analyseren. Er zijn twee datapunten (twee weken), die buiten de controlegrenzen vallen en daar moeten we verder onderzoek naar doen. Zoals ik al eerder zei, helpt de controlegrens ons te bepalen of corrigerende maatregelen nodig zijn of niet. Wanneer datapunten buiten de controlegrens vallen, toont dat aan dat de variabiliteit niet natuurlijk is.
Analyse van standaardafwijking en controlegrafiek stelt –
We hebben een slechte variatie. Hier, moeten wij de wortel van het probleem onderzoeken. Hiervoor kunnen we andere hulpmiddelen gebruiken, zoals “oorzaak en gevolg”-diagrammen, “Pareto-analyse”. Na analyse van de hoofdoorzaak en het nemen van corrigerende maatregelen, kunnen we het controlediagram opnieuw tekenen. En, komt te weten of de variatie met de tijd vermindert.
Eén cruciaal punt is dat aangezien wij speciale oorzaak moeten verwijderen, d.w.z. twee weken. We kunnen kiezen voor een brainstorming tool om te begrijpen –
Welke gebeurtenissen gehouden tijdens die twee weken bij te dragen aan speciale oorzaak variatie. In agile, kunnen wij dit in de Iteration retrospective doen. In dit geval zou het doel van iteratie, retrospective zijn om te bepalen wat we kunnen doen om het testproces onder controle te brengen.
Waarvoor wordt een controlekaart gebruikt?
Control Chart wordt gebruikt in “Plan Quality” om te begrijpen –
Wat er nodig is om ervoor te zorgen dat repeterende processen resultaten opleveren binnen aanvaardbare grenzen?
We ontwerpen het Procesverbeteringsplan dienovereenkomstig.
Kwaliteitsbeleid wordt verfijnd om de gewenste output te krijgen. En, metrieken worden gedefinieerd om de procesprestaties te meten. Historische verslagen van controlediagrammen spelen een belangrijke rol in de ontwikkeling van –
- procesverbeteringsplan,
- kwaliteitsbeheerplan, en
- kwaliteitsmetrieken.
Ook gebruiken wij de controlediagram als een hulpmiddel en techniek tijdens “Controle Kwaliteit” om te begrijpen –
of een zich herhalend proces resultaten binnen een aanvaardbaar bereik en op een willekeurige manier produceert.
Indien niet dan onderzoek moet worden uitgevoerd om speciale oorzaak variation.
In het kort, de controlegrafiek is een nuttig instrument om te begrijpen of een proces is stabiel met de tijd en het produceren van resultaten binnen aanvaardbare grenzen en op een willekeurige manier.
Ik hoop dat deze blog voldoende heeft beantwoord uw alle vragen met betrekking tot Control Chart. Good Luck met uw PMP ® Certificering Exam.
U kunt deelnemen aan de discussie over hetzelfde in ons Forum. U kunt ook inloggen op onze YouTube-kanaal bekijken van de video over hetzelfde.
Inschrijven op onze GRATIS PMP ®-certificering introductieprogramma om meer te leren over PMP ®-certificering