De eerste plot hierboven laat zien dat de grotere batchgroottes inderdaad minder afstand per epoch afleggen. De batch 32 training epoch afstand varieert van 0,15 tot 0,4, terwijl voor batch 256 training het ongeveer 0,02-0,04 is. Zoals we in de tweede grafiek kunnen zien, neemt de verhouding tussen de epoch-afstanden in de loop van de tijd toe!
Maar waarom legt een grote batch training minder afstand per epoch af? Is het omdat we minder batches hebben, en dus minder updates per epoch? Of is het omdat elke batch update minder afstand aflegt? Of is het antwoord een combinatie van beide?
Om deze vraag te beantwoorden, laten we de grootte van elke batch-update meten.

Median batch update norm for batch size 32: 3.3e-3
Median batch update norm for batch size 256: 1.5e-3
We kunnen zien dat elke batch-update kleiner is wanneer de batchgrootte groter is. Waarom zou dit het geval zijn?
Om dit gedrag te begrijpen, stellen we een dummy-scenario op, waarbij we twee gradiëntvectoren a en b hebben, die elk de gradiënt voor één trainingsvoorbeeld vertegenwoordigen. Laten we eens kijken hoe de gemiddelde grootte van de batch-update voor batchgrootte=1 zich verhoudt tot die van batchgrootte=2.

Als we een batchgrootte van één gebruiken, zetten we een stap in de richting van a, dan van b, om te eindigen op het punt dat wordt vertegenwoordigd door a+b. (Technisch gezien zou de gradiënt voor b opnieuw worden berekend na toepassing van a, maar laten we dat voor nu negeren). Dit resulteert in een gemiddelde batch-update grootte van (|a|+|b|)/2 – de som van de batch-updates, gedeeld door het aantal batch-updates.
Als we echter een batchgrootte van twee gebruiken, wordt de batch-update in plaats daarvan vertegenwoordigd door de vector (a+b)/2 – de rode pijl in figuur 12. De gemiddelde batch-update-grootte is dus |(a+b)/2| / 1 = |a+b|/2.
Nu vergelijken we de twee gemiddelde batch-update-groottes:

In de laatste regel hebben we de driehoeksongelijkheid gebruikt om aan te tonen dat de gemiddelde bijwerkingsgrootte voor batchgrootte 1 altijd groter of gelijk is aan die van batchgrootte 2.
Anders gezegd, om de gemiddelde bijwerkingsgrootte voor batchgrootte 1 en batchgrootte 2 gelijk te laten zijn, moeten de vectoren a en b in dezelfde richting wijzen, aangezien dat is wanneer |a| + |b| = |a+b|. We kunnen dit argument uitbreiden tot n vectoren – alleen wanneer alle n vectoren in dezelfde richting wijzen, zijn de gemiddelde batch update groottes voor batchgrootte=1 en batchgrootte=n gelijk. Dit is echter bijna nooit het geval, aangezien het onwaarschijnlijk is dat de gradiëntvectoren precies in dezelfde richting wijzen.

Als we terugkeren naar de minibatch update-vergelijking in figuur 16, zeggen we in zekere zin dat naarmate we de batchgrootte |B_k| opschalen, de grootte van de som van de gradiënten naar verhouding minder snel toeneemt. Dit is te wijten aan het feit dat de gradiëntvectoren in verschillende richtingen wijzen, en dus verdubbeling van de partijgrootte (d.w.z. het aantal gradiëntvectoren dat moet worden opgeteld) de grootte van de resulterende som van gradiëntvectoren niet verdubbelt. Tegelijkertijd delen we door een noemer |B_k| die twee keer zo groot is, wat resulteert in een kleinere update stap in totaal.
Dit zou kunnen verklaren waarom de batch updates voor grotere batchgroottes de neiging hebben om kleiner te zijn – de som van gradiënt vectoren wordt groter, maar kan de grotere noemer|B_k| niet volledig compenseren.
Hypothese 2: Kleine batch training vindt vlakkere minimalizers
Laten we nu de scherpte van beide minimalizers meten, en de bewering evalueren dat kleine batch training vlakkere minimalizers vindt. (Merk op dat deze tweede hypothese naast de eerste kan bestaan – ze sluiten elkaar niet uit). Om dit te doen lenen we twee methoden van Keskar et al.
In de eerste zetten we het trainings- en validatieverlies uit langs een lijn tussen een kleine-batch-minimalisator (batchgrootte 32) en een grote-batch-minimalisator (batchgrootte 256). Deze lijn wordt beschreven door de volgende vergelijking:

waarbij x_l* de grote partij-minimalisator is en x_s* de kleine partij-minimalisator, en alpha een coëfficiënt is tussen -1 en 2.

Zoals we in de grafiek kunnen zien, is de kleine-batch-minimalisator (alpha=0) veel vlakker dan de grote-batch-minimalisator (alpha=1), die veel sterker varieert.
Merk op dat dit een nogal simplistische manier is om scherpte te meten, aangezien slechts in één richting wordt gekeken. Daarom stellen Keskar et al een scherpte-metriek voor die meet hoeveel de verliesfunctie varieert in een buurt rond een minimalisator. Eerst definiëren we de buurt als volgt:

waarbij epsilon een parameter is die de grootte van de buurt bepaalt en x de minimizer is (de gewichten).
Dan definiëren we de scherpte metriek als het maximale verlies in deze buurt rond de minimalisator:

waarbij f de verliesfunctie is, met als invoer de gewichten.
Met bovenstaande definities berekenen we de scherpte van de minimalisatoren bij verschillende partijgroottes, met een epsilon-waarde van 1e-3:
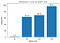
Dit toont aan dat de grote partijminimalisatoren inderdaad scherper zijn, zoals we zagen in de interpolatieplot.
Ten slotte kunnen we proberen de minimalisatoren te plotten met een filter-genormaliseerde verliesvisualisatie, zoals geformuleerd door Li et al. Dit type plot kiest twee willekeurige richtingen met dezelfde afmetingen als de modelgewichten, en normaliseert vervolgens elk convolutioneel filter (of neuron, in het geval van FC-lagen) om dezelfde norm te hebben als het corresponderende filter in de modelgewichten. Dit zorgt ervoor dat de scherpte van een minimalisator niet wordt beïnvloed door de grootte van zijn gewichten. Vervolgens wordt het verlies langs deze twee richtingen uitgezet, waarbij het middelpunt van de plot de minimalisator is die we willen karakteriseren.