>
ESTATA DOORDENADOR
Modelos de comutação Markov
>
Luzes altas
- >
- Modelos de comutação Markov-modelo de transição
- Modelo auto-regressivo
- Modelo de regressão dinâmica
- Parâmetros de regressão dependentes do estado
- Parâmetros de regressão dependentes do estadoparâmetros de variância dependente
- Tabelas de
- Probabilidades de transição
- Durações esperadas do estado
- Previsões
- Valores esperados da variável dependente
- Probabilidades de estar num estado
- Estático (umpasso)
- Dinâmico (multistep)
- RMSEs de previsões
De que se trata?
Por vezes, os processos evoluem ao longo do tempo com alterações discretas nos resultados.
Pense em recessões e expansões económicas. No início de uma recessão, a produção e o emprego caem e permanecem baixos e depois, mais tarde, a produção e o emprego aumentam. Pense nas desordens bipolares em que há períodos maníacos seguidos de períodos depressivos, e o processo se repete. Estatisticamente, as médias, variâncias e outros parâmetros estão mudando ao longo dos episódios (regimes). O nosso problema é estimar quando os regimes mudam e os valores dos parâmetros associados a cada regime. Perguntar quando os regimes mudam é equivalente a perguntar por quanto tempo os regimes persistem.
Nos modelos de Markov-transição, além de estimar as médias, variâncias, etc. de cada regime, estimamos também a probabilidade de mudança de regime. As probabilidades estimadas de transição para algum problema podem ser, as seguintes:
| de/para | ||
| >estado | 1 2 | |
| 1 | 0.82 0,18 | |
| 2 | 0,75 0,25 | |
Iniciar no estado 1. A probabilidade de transitar do estado 1 para o estado 1 é de 0,82. Dito de forma diferente, uma vez no estado 1, o processo tende a permanecer lá. Com probabilidade 0,18, entretanto, o processo transita para o estado 2. O estado 2 não é tão persistente. Com probabilidade 0,75, o processo reverte do estado 2 para o estado 1 no próximo período de tempo.
Os modelos de comutação de Markov não estão limitados a dois regimes, embora modelos de dois regimes sejam comuns.
No exemplo acima, descrevemos a comutação como sendo abrupta; a probabilidade mudou instantaneamente. Tais modelos de Markov são chamados modelos dinâmicos. Os modelos de Markov também podem acomodar mudanças mais suaves modelando as probabilidades de transição como um processo autoregressivo.
Assim, a comutação pode ser suave ou abrupta.
Vejamos como funciona
Vejamos as mudanças médias entre regimes. Em particular, vamos analisar a Taxa Federal de Fundos. A Taxa Federal de Fundos é a taxa de juros que o banco central dos EUA cobra dos bancos comerciais por empréstimos overnight. Vamos analisar as mudanças na taxa de fundos federais de 1954 até o final de 2010. Aqui estão os dados:
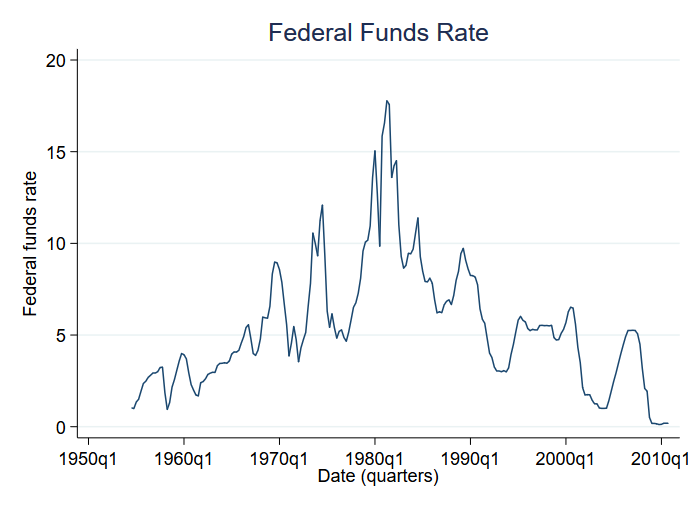
Temos dados trimestrais. As altas taxas de juros parecem caracterizar os anos setenta e oitenta. Vamos assumir que existe outro regime para taxas de juro mais baixas que parecem caracterizar as outras décadas.
Para encaixar um modelo de comutação dinâmica (mudança abrupta) com dois regimes, digitamos
. mswitch dr fedfundsPerforming EM optimizaton:Performing gradient-based optimization:
| Iteração 0: | probabilidade log = -508.66031 |
| Iteração 1: | verosimilhança log = -508.6382 |
| Iteração 2: | verosimilhança log = -508.63592 |
| Iteração 3: | verosimilhança log = -508.63592 |
Regressão dinâmica de comutação Markov Amostra: 1954q3 – 2010q4 Não. de obs = 226Número de estados = 2 AIC = 4.5455Probabilidades incondicionais: HQIC de transição = 4.5760 SBIC = 4.6211Probabilidade de log = -508,63592
| fedfunds | > Coef. Std. Err. z P>||z| | ||
| State1 | |||
| _cons | 3.70877 .1767083 20.99 0.000 3.362428 4.055112 | ||
| State2 | |||
| _cons | 9,556793 .2999889 31,86 0,000 8,968826 10,14476 | ||
| 2,107562 .1008692 1,918851 2.314831 | |||
| p11 | .9820939 .0104002 .9450805 .9943119 | ||
| p21 | .0503587 .0268434 .0173432 .1374344 | ||
Reportados na saída acima são
- as médias dos dois estados (_cons);
- um único desvio padrão para todo o processo (sigma); e
- as probabilidades de transição para o estado 1 para 1 e estado 2 para 1 (p11 e p21).
State1 é o estado de taxa moderada (média de 3,71%).
State2 é o estado de taxa alta (média de 9,56%).
| de/para | ||
| estado | 1 2 | |
| 1 | 0.98 1 – 0,98 | |
| 2 | 0,05 1 – 0,05 | |
Ambos os estados são incrivelmente persistentes (1->1 e 2->2 probabilidades de 0,98 e 0,95).
Entre as coisas que você pode prever após a estimativa está a probabilidade de estar nos vários estados. Temos apenas dois estados, e assim a probabilidade de estar no (digamos) estado 2 diz-nos a probabilidade de estar nos dois estados. Podemos obter a probabilidade prevista e fazer um gráfico junto com os dados originais:
. predict prfed, pr
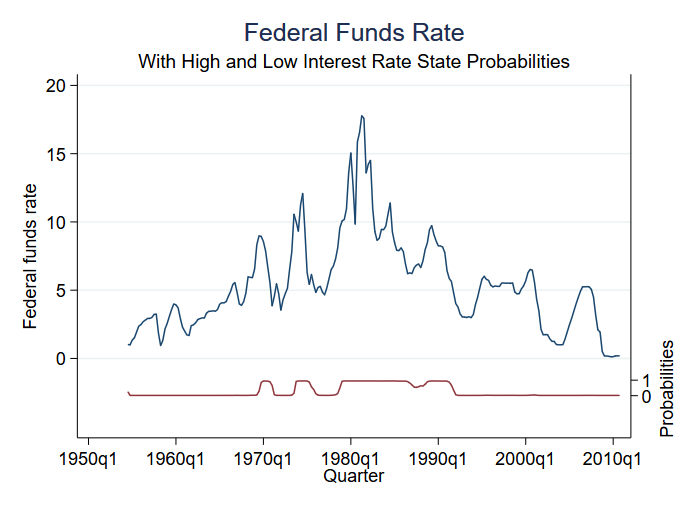
O modelo tem pouca incerteza quanto ao regime em cada momento. Vemos três períodos de estados de taxa elevada e quatro períodos de estados de taxa moderada.
Vejamos o seu funcionamento
Vejamos um exemplo de surto de doença, nomeadamente papeira por 10.000 residentes na cidade de Nova Iorque entre 1929 e 1972. Você pode pensar que surtos correspondem a mudanças significativas, mas o que vemos nos dados é uma mudança ainda maior na variância:
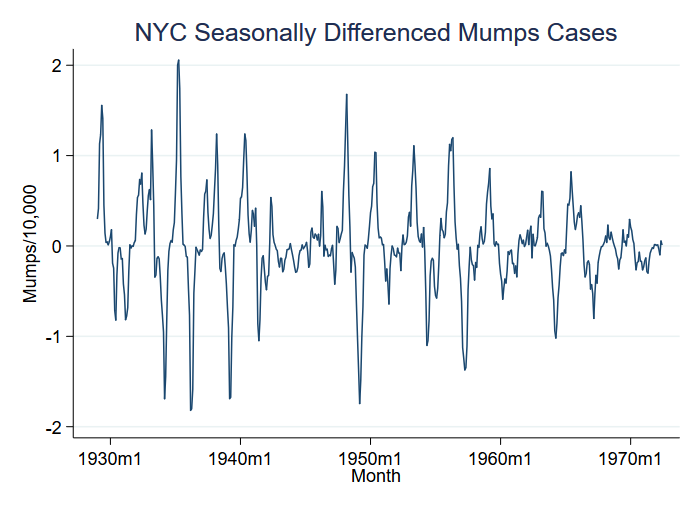
Pegamos a variável S12.mumpspc, significando casos de papeira per capita sazonalmente diferentes durante um período de 12 meses, e vamos analisar a S12.mumpspc.
Vamos assumir dois regimes em que a média e a variância da S12.mumpspc mudam. Para ajustar um modelo dinâmico (mudança brusca), vamos digitar
. mswitch dr S12.mumpspc, varswitch switch(LS12.mumpspc, noconstant)Performing EM optimizaton:Performing gradient-based optimization:
| Iteração 0: | verosimilhança log = 110,9372 (não côncava) |
| Iteração 1: | verosimilhança log = 120.68028 |
| Iteração 2: | verosimilhança log = 123,23244 |
| Iteração 3: | verosimilhança log = 131,47084 |
| Iteração 3: | verosimilhança log = 131.72182 |
| Iteração 3: | verosimilhança log = 131,7225 |
| Iteração 3: | verosimilhança log = 131,7225 |
Regressão dinâmica de comutação Markov Amostra: 1929m2 – 1972m6 Não. de obs = 521Número de estados = 2 AIC = -0,4826Probabilidades incondicionais: HQIC de transição = -0,4634 SBIC = -0,4336Probabilidade de log = 131,7225
| S12.mumspc | Coef. Std. Err. z P>||z| | ||
| State1 | |||
| mumpspc | |||
| LS12. | .4202751 .0167461 25.10 0.000 .3874533 .4530968 | ||
| State2 | |||
| mumpspc | |||
| LS12. | .9847369 .0258383 38.11 0.000 .9340947 1.035379 | ||
| sigma1 | .0562405 .0050954 .0470901 .067169 | ||
| sigma2 | .2611362 .0111191 .2402278 .2838644 | ||
| p11 | .762733 .0362619 .6846007 .8264175 | ||
| p12 | .1473767 .0257599 .1036675 .205294 | ||
>
Reportados são
- os meios dos dois estados de S12.mumpspc (0,42 e 0,98);
- os desvios padrão dos dois estados (0,06 e 0,26); e
- as probabilidades de transição para o estado 1 para 1 e estado 2 para 1 (0,76 e 0,15).
o estado 1 é o estado de baixa variância.
O conjunto completo de probabilidades de transição é o seguinte: