Análise de dados ¶
Dado um conjunto de dados, pode-se usar o método fit para estimar uma transformada branqueadora.
fit(Branqueamento, X; …)¶
Estimar uma transformada branqueadora a partir dos dados fornecidos em X. Aqui, X deve ser uma matriz, cujas colunas dão as amostras.
Esta função retorna uma instância de Whitening.
Argumentos de palavras-chave:
| nome | descrição | default |
|---|---|---|
| regcoef |
O coeficiente de regularização. A covariância será regularizada da seguinte forma quando
|
zero(T) |
| significativo |
O vector médio, que pode ser de:
|
nothing |
Nota: Esta função depende internamente de cov_whiten para derivar a transformação W. A própria função cov_whiten é também uma função útil.
cov_whitening(C)¶
Derivar a matriz de coeficiente de transformação branqueadora W dada a matriz de covariância C. Aqui, C pode ser uma matriz quadrada, ou uma instância de Cholesky.
Internamente, esta função resolve a transformada branqueadora usando a factorização Cholesky. A lógica é a seguinte: let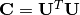 
e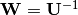 
, depois 
.
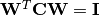Nota: A matriz de retorno W é uma matriz triangular superior.
cov_whitening(C, regcoef)
Executar uma transformação branqueadora baseada em uma covariância regularizada, como C + (eigmax(C) * regcoef) * eye(d).
Além disso, o pacote também fornece cov_whiten!, no qual a matriz de entrada C será sobregravada durante o cálculo. Isto pode ser mais eficiente quando C não é mais usado.
invsqrtm(C)¶
Compute inv(sqrtm(C)) através da decomposição simétrica do autovalor.