O primeiro gráfico acima mostra que os tamanhos maiores dos lotes atravessam de fato menos distância por época. A distância do lote 32 de treinamento varia de 0,15 a 0,4, enquanto que para o lote 256 de treinamento fica em torno de 0,02-0,04. Na verdade, como podemos ver no segundo gráfico, a proporção das distâncias entre as épocas aumenta com o tempo!
Mas por que o treinamento em lotes grandes percorre menos distância por época? Será porque temos menos lotes, e portanto menos atualizações por época? Ou será porque cada atualização de lote percorre menos distância? Ou, a resposta é uma combinação de ambos?
Para responder a esta pergunta, vamos medir o tamanho de cada atualização de lote.

Median batch update norm for batch size 32: 3.3e-3
Median batch update norm for batch size 256: 1.5e-3
Vemos que cada atualização de lote é menor quando o tamanho do lote é maior. Por que seria este o caso?
Para entender este comportamento, vamos montar um cenário fictício, onde temos dois vetores de gradiente a e b, cada um representando o gradiente para um exemplo de treinamento. Vamos pensar em como o tamanho médio de atualização do lote para o tamanho do lote=1 se compara com o tamanho do lote=2.

Se usarmos um tamanho de lote de um, daremos um passo na direção de a, então b, terminando no ponto representado por a+b. (Tecnicamente, o gradiente para b seria recalculado após a aplicação de a, mas vamos ignorar isso por enquanto). Isto resulta em um tamanho médio de atualização do lote de (|a|+|b|)/2 – a soma dos tamanhos de atualização do lote, dividida pelo número de atualizações do lote.
No entanto, se usarmos um tamanho de lote de dois, a atualização do lote é representada pelo vetor (a+b)/2 – a seta vermelha na Figura 12. Assim, o tamanho médio de atualização do lote é |(a+b)/2| / 1 = |a+b|/2.
Agora, vamos comparar os dois tamanhos médios de atualização do lote:

Na última linha, usamos a desigualdade triangular para mostrar que o tamanho médio de atualização do lote 1 é sempre maior ou igual ao tamanho do lote 2,
Cortar de outra forma, para que o tamanho médio do lote 1 e do lote 2 sejam iguais, os vetores a e b devem estar apontando na mesma direção, já que é quando |a| + |b| = |a+b|. Podemos estender este argumento para n vectores – apenas quando todos os n vectores estão a apontar na mesma direcção, são os tamanhos médios de actualização do lote para o tamanho do lote=1 e o tamanho do lote=n o mesmo. No entanto, este quase nunca é o caso, uma vez que os vetores de gradiente são improváveis de apontar exatamente na mesma direção.

Se voltarmos à equação de atualização do lote minibatch na Figura 16, estamos de certa forma dizendo que à medida que aumentamos o tamanho do lote |B_k|, a magnitude da soma dos gradientes aumenta comparativamente menos rapidamente. Isto se deve ao fato de que os vetores de gradiente apontam em diferentes direções, e assim duplicar o tamanho do lote (ou seja, o número de vetores de gradiente para somar juntos) não duplica a magnitude da soma resultante dos vetores de gradiente. Ao mesmo tempo, estamos dividindo por um denominador |B_k| que é duas vezes maior, resultando em um passo de atualização menor em geral.
Isso poderia explicar porque as atualizações do lote para lotes maiores tendem a ser menores – a soma dos vetores de gradiente torna-se maior, mas não pode compensar totalmente o denominador maior|B_k|.
Hypothesis 2: Treinamento em lotes pequenos encontra minimizadores mais achatados
Vamos agora medir a nitidez de ambos os minimizadores, e avaliar a alegação de que o treinamento em lotes pequenos encontra minimizadores mais achatados. (Note que esta segunda hipótese pode coexistir com a primeira – eles não são mutuamente exclusivos). Para isso, pedimos dois métodos emprestados a Keskar et al.
Na primeira, plotamos a perda de treinamento e validação ao longo de uma linha entre um minimizador de lotes pequenos (tamanho de lote 32) e um minimizador de lotes grandes (tamanho de lote 256). Esta linha é descrita pela seguinte equação:

onde x_l* é o minimizador de lote grande e x_s* é o minimizador de lote pequeno, e alfa é um coeficiente entre -1 e 2,

Como podemos ver no gráfico, o minimizador de lotes pequenos (alpha=0) é muito mais plano que o minimizador de lotes grandes (alpha=1), que varia muito mais acentuadamente.
Notem que esta é uma forma bastante simplista de medir a nitidez, uma vez que considera apenas uma direcção. Assim, Keskar et al propõem uma métrica de nitidez que mede o quanto a função de perda varia em uma vizinhança em torno de um minimizador. Primeiro, definimos a vizinhança da seguinte forma:

onde epsilon é um parâmetro que define o tamanho da vizinhança e x é o minimizador (os pesos).
Então, definimos a métrica de nitidez como a perda máxima nesta vizinhança em torno do minimizador:

onde f é a função de perda, sendo os inputs os pesos.
Com as definições acima, vamos calcular a nitidez dos minimizadores em vários tamanhos de lote, com um valor epsilon de 1e-3:
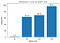
Isto mostra que os minimizadores de grandes lotes são de facto mais nítidos, como vimos no gráfico da interpolação.
Por último, vamos tentar plotar os minimizadores com uma visualização de perdas com filtro-normalizada, como formulado por Li et al . Este tipo de gráfico escolhe duas direções aleatórias com as mesmas dimensões dos pesos do modelo, e depois normaliza cada filtro convolutivo (ou neurônio, no caso de camadas FC) para ter a mesma norma que o filtro correspondente nos pesos do modelo. Isto garante que a nitidez de um minimizador não seja afetada pela magnitudes de seus pesos. Em seguida, ele traça a perda ao longo destas duas direções, sendo o centro da trama o minimizador que desejamos caracterizar.