Um percentil é uma localização numa distribuição que tem uma quantidade especificada (ou percentagem) da distribuição “abaixo dela” (à sua esquerda). Em outras palavras, se o percentil #n^”th “# for #x#, e tirarmos um número aleatório #X# da distribuição, então a chance de #X# ser menor que #x# é #n %#:
#n^”th” ” percentil” = x”. ” P(X x)=n%.#
Por exemplo, numa curva normal (com #mu = 0# e #sigma = 1#), o ponto onde #x=0# (i.e. o eixo #y#) é o percentil 50, porque 50% da área da curva cai para a esquerda de #x=0#:

A distribuição normal padrão #Z# é uma linha de base tão boa, na verdade temos uma tabela de valores desenhada especificamente para procurar percentis acima para esta curva. É chamada de #z#-table, e parece algo assim:
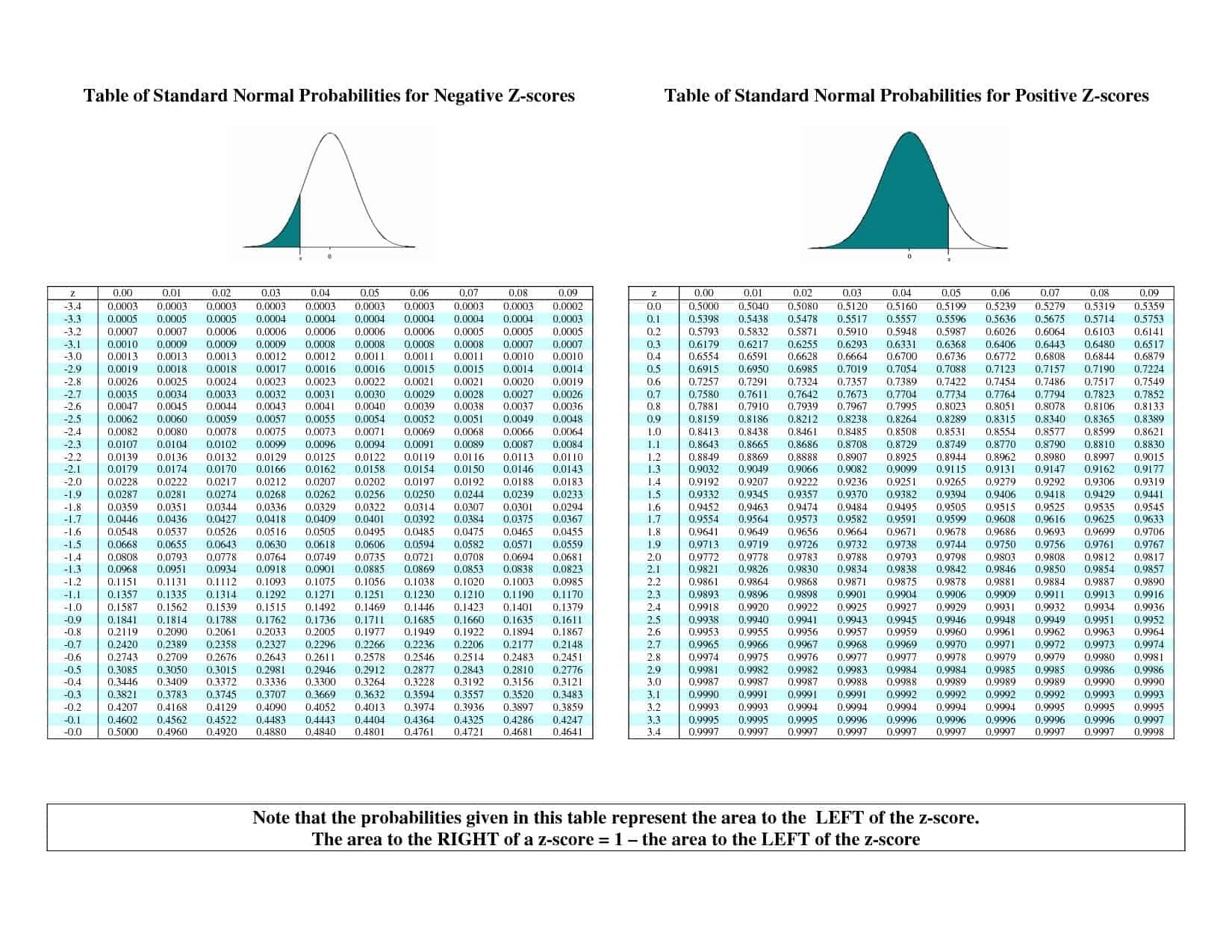
Como a usamos? Digamos que queremos o percentil 25 para a distribuição normal normal. Encontramos o valor mais próximo de 0,25 na tabela (que por acaso é 0,2514) e vemos que está na linha #”-“0,6# e na coluna #0,07#. Para esta tabela, isso significa que o percentil 25 é (aproximadamente) #”-“0.67#.
Mas espere, como isso ajuda quando queremos um percentil para qualquer distribuição normal #X#? Precisamos de encontrar uma ligação entre qualquer curva e a curva normal padrão. Essa conexão é encontrada deslocando a distribuição #X# da esquerda para a direita para que fique centrada em #0#, e depois esticando-a/esquadrando-a para que seu desvio padrão seja #1#. A fórmula para isto é:
#Z=(X-mu)/sigma#
onde #mu# é a média de #X# e #sigma# é a s.d. de #X#.
>
Se sabemos o percentil que queremos da distribuição #Z#, podemos resolver para #X# reordenando a equação em
>
#X=sigma Z + mu#.
Como exemplo, vamos usar a primeira pergunta que você fez, onde #X# é normalmente distribuído com #mu = 81,2# e #sigma = 12,4#, e procuramos o percentil 16.
Da tabela acima, o percentil 16 da distribuição #Z# é aproximadamente #”-“0,99#. A localização equivalente na nossa distribuição #X# é então:
#X=(12.4)(“-“0.99)+81.2#
#color(white)X=”-“12.276+81.2#
#color(branco)X=68.924#
O que isto diz é: se #X# é uma curva normal com #mu=81.2 ” pés “# e #sigma = 12.4 ” feet “#, então há 16% de chance de uma observação de #X# ser inferior a #68.924 ” feet “#.
Eu deixo o resto para você como um exercício; com as fórmulas acima, não deve ser tão difícil.
Espera que isto ajude!