Order STATA
Markov-Switching-Modelle
Highlights
- Markov-.Übergangsmodellierung
- Autoregressives Modell
- Dynamisches Regressionsmodell
- Zustandsabhängige Regressionsparameter
- Zustands-.zustandsabhängige Varianzparameter
- Tabellen mit
- Übergangswahrscheinlichkeiten
- Erwartete Zustandsdauern
- Vorhersagen
- Erwartete Werte der abhängigen Variablen
- Zustandswahrscheinlichkeiten
- Statisch (ein-Schritt)
- Dynamisch (mehrstufig)
- RMSEs der Vorhersagen
Worum geht es hier?
Manchmal entwickeln sich Prozesse im Laufe der Zeit mit diskreten Veränderungen der Ergebnisse.
Man denke an wirtschaftliche Rezessionen und Expansionen. Zu Beginn einer Rezession sinken Produktion und Beschäftigung und bleiben auf niedrigem Niveau, später steigen Produktion und Beschäftigung wieder an. Denken Sie an bipolare Störungen, bei denen auf manische Phasen depressive Phasen folgen, und der Prozess wiederholt sich. Statistisch gesehen ändern sich Mittelwerte, Varianzen und andere Parameter zwischen den Episoden (Regimen). Unser Problem besteht darin, zu schätzen, wann sich die Regime ändern und welche Werte die Parameter haben, die mit jedem Regime verbunden sind. Die Frage, wann sich Regime ändern, ist gleichbedeutend mit der Frage, wie lange Regime andauern.
In Markov-Übergangsmodellen werden nicht nur die Mittelwerte, Varianzen usw. der einzelnen Regime geschätzt, sondern auch die Wahrscheinlichkeit eines Regimewechsels. Die geschätzten Übergangswahrscheinlichkeiten für ein bestimmtes Problem könnten wie folgt aussehen:
| vom/zum | ||
| Zustand | 1 2 | |
| 1 | 0.82 0,18 | |
| 2 | 0,75 0,25 | |
Start im Zustand 1. Die Wahrscheinlichkeit des Übergangs von Zustand 1 zu Zustand 1 beträgt 0,82. Anders ausgedrückt: Ist der Prozess einmal im Zustand 1, neigt er dazu, dort zu bleiben. Mit einer Wahrscheinlichkeit von 0,18 geht der Prozess jedoch in den Zustand 2 über. Der Zustand 2 ist nicht so beständig. Mit einer Wahrscheinlichkeit von 0,75 kehren die Prozesse in der nächsten Zeitperiode von Zustand 2 zu Zustand 1 zurück.
Markov-Switching-Modelle sind nicht auf zwei Zustände beschränkt, obwohl Modelle mit zwei Zuständen üblich sind.
Im obigen Beispiel haben wir den Wechsel als abrupt beschrieben; die Wahrscheinlichkeit änderte sich augenblicklich. Solche Markov-Modelle werden als dynamische Modelle bezeichnet. Markov-Modelle können auch sanftere Veränderungen berücksichtigen, indem sie die Übergangswahrscheinlichkeiten als autoregressiven Prozess modellieren.
Somit kann der Übergang sanft oder abrupt sein.
Lassen Sie uns sehen, wie es funktioniert
Betrachten wir die mittleren Veränderungen zwischen den Regimen. Im Besonderen werden wir die Federal Funds Rate analysieren. Die Federal Funds Rate ist der Zinssatz, den die Zentralbank der USA den Geschäftsbanken für Übernachtkredite berechnet. Wir werden uns die Veränderungen der Federal Funds Rate von 1954 bis Ende 2010 ansehen. Hier sind die Daten:
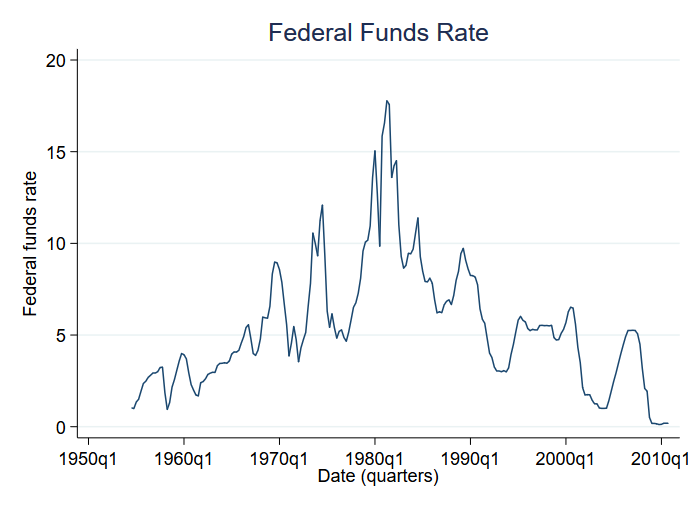
Wir haben vierteljährliche Daten. Hohe Zinssätze scheinen die siebziger und achtziger Jahre zu kennzeichnen. Wir nehmen an, dass es ein weiteres Regime für niedrige Zinssätze gibt, das die anderen Jahrzehnte zu charakterisieren scheint.
Um ein Dynamic-Switching-Modell (abrupte Änderung) mit zwei Regimen anzupassen, geben wir
. mswitch dr fedfundsPerforming EM optimizaton:Performing gradient-based optimization:
| Iteration 0: | log likelihood = -508.66031 |
| Iteration 1: | log Likelihood = -508.6382 |
| Iteration 2: | log Likelihood = -508.63592 |
| Iteration 3: | log likelihood = -508.63592 |
Markov-switching dynamic regressionSample: 1954q3 – 2010q4 No. der Beobachtungen = 226Anzahl der Zustände = 2 AIC = 4,5455Unbedingte Wahrscheinlichkeiten: Übergang HQIC = 4,5760 SBIC = 4,6211Log Likelihood = -508.63592
| fedfunds | Coef. Std. Err. z P>|z| | ||
| State1 | |||
| _cons | 3.70877 .1767083 20.99 0.000 3.362428 4.055112 | ||
| State2 | |||
| _cons | 9.556793 .2999889 31.86 0.000 8.968826 10.14476 | ||
| sigma | 2.107562 .1008692 1.918851 2.314831 | ||
| p11 | .9820939 .0104002 .9450805 .9943119 | ||
| p21 | .0503587 .0268434 .0173432 .1374344 | ||
In der obigen Ausgabe werden
- die Mittelwerte der beiden Zustände (_cons);
- eine einzelne Standardabweichung für den gesamten Prozess (sigma); und
- die Übergangswahrscheinlichkeiten für Zustand 1 zu 1 und Zustand 2 zu 1 (p11 und p21) angegeben.
Zustand1 ist der mittelmäßige Zustand (Mittelwert von 3,71 %).
Zustand2 ist der hochgradige Zustand (Mittelwert 9,56 %).
| von/nach | ||
| Staat | 1 2 | |
| 1 | 0.98 1 – 0.98 | |
| 2 | 0.05 1 – 0.05 | |
Beide Zustände sind unglaublich persistent (1->1 und 2->2 Wahrscheinlichkeiten von 0.98 und 0.95).
Zu den Dingen, die man nach der Schätzung vorhersagen kann, gehört die Wahrscheinlichkeit, sich in den verschiedenen Zuständen zu befinden. Es gibt nur zwei Zustände, so dass die Wahrscheinlichkeit, sich in (sagen wir) Zustand 2 zu befinden, die Wahrscheinlichkeit für beide Zustände angibt. Wir können die vorhergesagte Wahrscheinlichkeit erhalten und sie zusammen mit den ursprünglichen Daten grafisch darstellen:
. predict prfed, pr
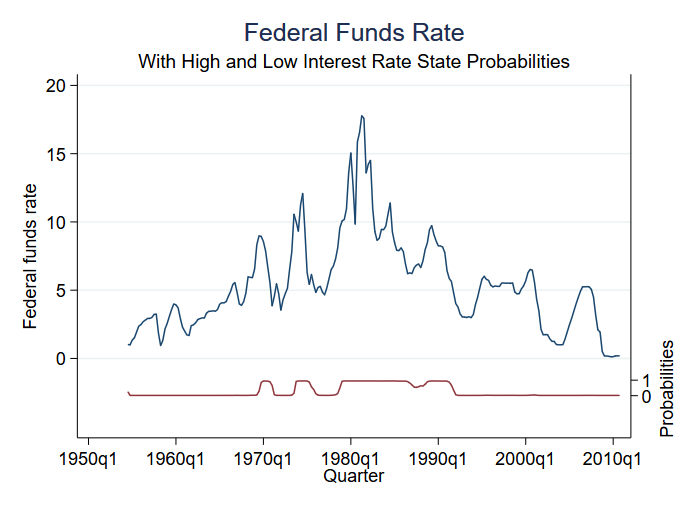
Das Modell weist zu jedem Zeitpunkt eine geringe Unsicherheit hinsichtlich des Regimes auf. Wir sehen drei Perioden mit hohen Raten und vier Perioden mit moderaten Raten.
Lassen Sie uns sehen, wie es funktioniert
Betrachten wir ein Beispiel eines Krankheitsausbruchs, nämlich Mumps pro 10.000 Einwohner in New York City zwischen 1929 und 1972. Man könnte meinen, dass Ausbrüche mit Veränderungen des Mittelwerts einhergehen, aber was wir in den Daten sehen, ist eine noch größere Veränderung der Varianz:
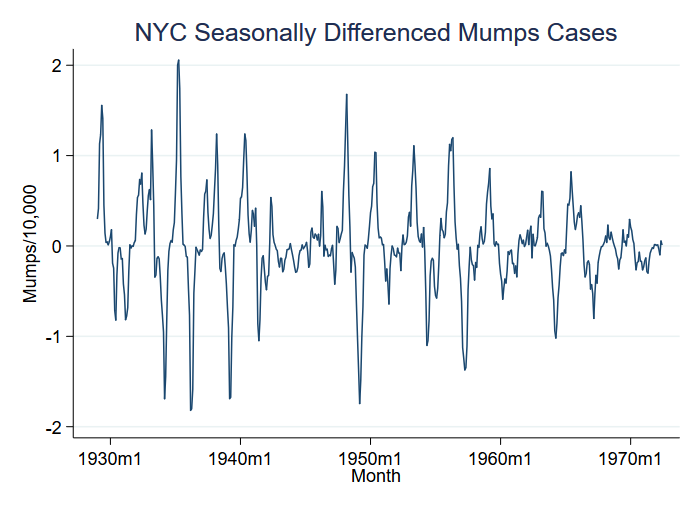
Wir haben die Variable S12.mumpspc, d. h. die saisonal differenzierten Mumpsfälle pro Kopf über einen Zeitraum von 12 Monaten, grafisch dargestellt und werden S12.mumpspc nun analysieren.
Wir werden von zwei Regimen ausgehen, in denen sich der Mittelwert und die Varianz von S12.mumpspc ändern. Um ein dynamisches Modell (mit abrupter Änderung) anzupassen, geben wir
. mswitch dr S12.mumpspc, varswitch switch(LS12.mumpspc, noconstant)Performing EM optimizaton:Performing gradient-based optimization:
| Iteration 0: | log likelihood = 110.9372 (nicht konkav) |
| Iteration 1: | log likelihood = 120.68028 |
| Iteration 2: | log likelihood = 123.23244 |
| Iteration 3: | log likelihood = 131.47084 |
| Iteration 3: | log likelihood = 131.72182 |
| Iteration 3: | log Likelihood = 131.7225 |
| Iteration 3: | log Likelihood = 131.7225 |
Markov-switching dynamic regressionSample: 1929m2 – 1972m6 No. der Beobachtungen = 521Anzahl der Zustände = 2 AIC = -0.4826Unbedingte Wahrscheinlichkeiten: Übergang HQIC = -0.4634 SBIC = -0.4336Likelihood = 131.7225
| S12.mumspc | Coef. Std. Err. z P>|z| | |
| State1 | ||
| mumpspc | ||
| LS12. | .4202751 .0167461 25.10 0.000 .3874533 .4530968 | |
| State2 | ||
| mumpspc | ||
| LS12. | .9847369 .0258383 38.11 0.000 .9340947 1.035379 | |
| sigma1 | .0562405 .0050954 .0470901 .067169 | |
| sigma2 | .2611362 .0111191 .2402278 .2838644 | |
| p11 | .762733 .0362619 .6846007 .8264175 | |
| p12 | .1473767 .0257599 .1036675 .205294 | |
Angegeben sind
- die Mittelwerte der beiden Zustände von S12.mumpspc (0,42 und 0,98);
- die Standardabweichungen der beiden Zustände (0,06 und 0,26); und
- die Übergangswahrscheinlichkeiten für Zustand 1 zu 1 und Zustand 2 zu 1 (0,76 und 0,15).
Zustand 1 ist der Zustand mit geringer Varianz.
Der vollständige Satz von Übergangswahrscheinlichkeiten ist der folgende: