Das erste Diagramm oben zeigt, dass die größeren Stapelgrößen tatsächlich eine geringere Entfernung pro Epoche zurücklegen. Der Abstand der Trainingsepoche bei Batch 32 schwankt zwischen 0,15 und 0,4, während er bei Batch 256 etwa 0,02-0,04 beträgt. Wie im zweiten Diagramm zu sehen ist, nimmt das Verhältnis der Epochenabstände im Laufe der Zeit sogar zu!
Warum aber wird beim Training mit großen Stapeln eine geringere Strecke pro Epoche zurückgelegt? Liegt es daran, dass wir weniger Batches und damit weniger Updates pro Epoche haben? Oder liegt es daran, dass jede Stapelaktualisierung eine geringere Entfernung zurücklegt? Oder ist die Antwort eine Kombination aus beidem?
Um diese Frage zu beantworten, messen wir die Größe der einzelnen Batch-Updates.

Median batch update norm for batch size 32: 3.3e-3
Median batch update norm for batch size 256: 1.5e-3
Wir können sehen, dass jedes Batch-Update kleiner ist, wenn die Batch-Größe größer ist. Warum ist dies der Fall?
Um dieses Verhalten zu verstehen, stellen wir ein Dummy-Szenario auf, in dem wir zwei Gradientenvektoren a und b haben, die jeweils den Gradienten für ein Trainingsbeispiel darstellen. Überlegen wir uns, wie die durchschnittliche Größe der Stapelaktualisierung bei Stapelgröße 1 im Vergleich zu der von Stapelgröße 2 ist.

Wenn wir eine Chargengröße von eins verwenden, machen wir einen Schritt in Richtung a, dann b und landen schließlich an dem Punkt, der durch a+b dargestellt wird. (Technisch gesehen würde der Gradient für b nach der Anwendung von a neu berechnet werden, aber lassen wir das erst einmal außer Acht). Daraus ergibt sich eine durchschnittliche Stapelaktualisierungsgröße von (|a|+|b|)/2 – die Summe der Stapelaktualisierungsgrößen, geteilt durch die Anzahl der Stapelaktualisierungen.
Wenn wir jedoch eine Stapelgröße von zwei verwenden, wird die Stapelaktualisierung stattdessen durch den Vektor (a+b)/2 dargestellt – der rote Pfeil in Abbildung 12. Die durchschnittliche Chargenaktualisierungsgröße ist also |(a+b)/2| / 1 = |a+b|/2.
Lassen Sie uns nun die beiden durchschnittlichen Chargenaktualisierungsgrößen vergleichen:

In der letzten Zeile haben wir die Dreiecksungleichung verwendet, um zu zeigen, dass die durchschnittliche Losgröße für Losgröße 1 immer größer oder gleich der für Losgröße 2 ist.
Mit anderen Worten: Damit die durchschnittliche Losgröße für Losgröße 1 und Losgröße 2 gleich ist, müssen die Vektoren a und b in dieselbe Richtung zeigen, denn dann ist |a| + |b| = |a+b|. Wir können dieses Argument auf n Vektoren ausdehnen – nur wenn alle n Vektoren in dieselbe Richtung zeigen, sind die durchschnittlichen Chargenaktualisierungsgrößen für Chargengröße 1 und Chargengröße n gleich. Dies ist jedoch fast nie der Fall, da es unwahrscheinlich ist, dass die Gradientenvektoren genau in die gleiche Richtung zeigen.

Wenn wir zur Minibatch-Aktualisierungsgleichung in Abbildung 16 zurückkehren, sagen wir in gewissem Sinne, dass mit zunehmender Losgröße |B_k| die Summe der Gradienten vergleichsweise weniger schnell ansteigt. Das liegt daran, dass die Gradientenvektoren in unterschiedliche Richtungen zeigen, so dass eine Verdopplung der Stapelgröße (d. h. der Anzahl der zu summierenden Gradientenvektoren) nicht zu einer Verdopplung des Betrags der resultierenden Summe der Gradientenvektoren führt. Gleichzeitig dividieren wir durch einen doppelt so großen Nenner |B_k|, was insgesamt zu einem kleineren Aktualisierungsschritt führt.
Dies könnte erklären, warum die Stapelaktualisierungen für größere Stapelgrößen tendenziell kleiner sind – die Summe der Gradientenvektoren wird größer, kann aber den größeren Nenner|B_k| nicht vollständig ausgleichen.
Hypothese 2: Training mit kleinen Stapeln findet flachere Minimierer
Lassen Sie uns nun die Schärfe beider Minimierer messen und die Behauptung bewerten, dass Training mit kleinen Stapeln flachere Minimierer findet. (Beachten Sie, dass diese zweite Hypothese mit der ersten koexistieren kann – sie schließen sich nicht gegenseitig aus.) Zu diesem Zweck leihen wir uns zwei Methoden von Keskar et al.
Bei der ersten Methode zeichnen wir den Trainings- und Validierungsverlust entlang einer Linie zwischen einem Small-Batch-Minimizer (Losgröße 32) und einem Large-Batch-Minimizer (Losgröße 256) auf. Diese Linie wird durch die folgende Gleichung beschrieben:

wobei x_l* der Minimierer der großen Charge und x_s* der Minimierer der kleinen Charge ist und alpha ein Koeffizient zwischen -1 und 2 ist.

Wie in der Grafik zu sehen ist, ist der kleine Batch-Minimierer (alpha=0) viel flacher als der große Batch-Minimierer (alpha=1), der viel stärker variiert.
Bei dieser Messung der Schärfe ist zu beachten, dass sie sehr vereinfacht ist, da sie nur eine Richtung berücksichtigt. Daher schlagen Keskar et al. eine Schärfe-Metrik vor, die misst, wie stark die Verlustfunktion in einer Nachbarschaft um einen Minimierer herum variiert. Zunächst definieren wir die Nachbarschaft wie folgt:

wobei epsilon ein Parameter ist, der die Größe der Nachbarschaft definiert und x der Minimierer (die Gewichte) ist.
Dann definieren wir die Schärfe-Metrik als den maximalen Verlust in dieser Nachbarschaft um den Minimierer:

wobei f die Verlustfunktion ist, wobei die Eingaben die Gewichte sind.
Mit den obigen Definitionen berechnen wir die Schärfe der Minimierer bei verschiedenen Losgrößen mit einem Epsilon-Wert von 1e-3:
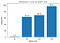
Dies zeigt, dass die großen Chargenminimierer tatsächlich schärfer sind, wie wir in der Interpolationsdarstellung gesehen haben.
Zuletzt wollen wir versuchen, die Minimierer mit einer filter-normalisierten Verlustvisualisierung darzustellen, wie sie von Li et al. formuliert wurde. Bei dieser Art der Darstellung werden zwei zufällige Richtungen mit denselben Dimensionen wie die Modellgewichte gewählt, und dann wird jeder Faltungsfilter (oder jedes Neuron, im Falle von FC-Schichten) so normalisiert, dass er dieselbe Norm wie der entsprechende Filter in den Modellgewichten hat. Dadurch wird sichergestellt, dass die Schärfe einer Minimierung nicht durch die Größe ihrer Gewichte beeinflusst wird. Anschließend wird der Verlust entlang dieser beiden Richtungen aufgetragen, wobei der Mittelpunkt der Darstellung der zu charakterisierende Minimierer ist.