Data Analysis¶
Gegeben einen Datensatz, kann man die Methode fit verwenden, um eine Whitening-Transformation zu schätzen.
fit(Whitening, X; …)¶
Schätzen Sie eine Whitening-Transformation aus den in X angegebenen Daten. Hier sollte X eine Matrix sein, deren Spalten die Stichproben angeben.
Diese Funktion gibt eine Instanz von Whitening zurück.
Schlüsselwortargumente:
| Name | Beschreibung | Standard |
|---|---|---|
| regcoef |
der Regularisierungskoeffizient. Die Kovarianz wird wie folgt regularisiert, wenn
|
zero(T) |
| Mittelwert |
Der Mittelwertvektor, der einer der folgenden sein kann:
|
nothing |
Anmerkung: Diese Funktion stützt sich intern auf cov_whiten, um die Transformation W abzuleiten. Die Funktion cov_whiten selbst ist ebenfalls eine nützliche Funktion.
cov_whitening(C)¶
Leitet die Koeffizientenmatrix W der Weißwandtransformation aus der Kovarianzmatrix C ab. Dabei kann C entweder eine quadratische Matrix oder eine Instanz von Cholesky sein.
Intern löst diese Funktion die Whitening-Transformation mittels Cholesky-Faktorisierung. Der Grundgedanke ist folgender: Sei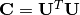 
und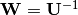 
, dann 
.
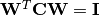Hinweis: Die Rückgabematrix W ist eine obere Dreiecksmatrix.
cov_whitening(C, regcoef)
Leitet eine Whitening-Transformation basierend auf einer regularisierten Kovarianz ab, wie C + (eigmax(C) * regcoef) * eye(d).
Zusätzlich bietet das Paket auch cov_whiten!, bei dem die Eingabematrix C während der Berechnung überschrieben wird. Dies kann effizienter sein, wenn C nicht mehr verwendet wird.
invsqrtm(C)¶
Berechnen Sie inv(sqrtm(C)) durch symmetrische Eigenwertzerlegung.