Primul grafic de mai sus arată că mărimile mai mari ale loturilor parcurg într-adevăr o distanță mai mică pe epocă. Distanța epocii de formare a lotului 32 variază de la 0,15 la 0,4, în timp ce pentru formarea lotului 256 este de aproximativ 0,02-0,04. De fapt, după cum putem vedea în cel de-al doilea grafic, raportul dintre distanțele epocii crește în timp!
Dar de ce parcurge o distanță mai mică pe epocă antrenamentul pe loturi mari? Este din cauză că avem mai puține loturi și, prin urmare, mai puține actualizări pe epocă? Sau este pentru că fiecare actualizare a lotului parcurge o distanță mai mică? Sau, răspunsul este o combinație a ambelor?
Pentru a răspunde la această întrebare, să măsurăm dimensiunea fiecărei actualizări pe loturi.

Median batch update norm for batch size 32: 3.3e-3
Median batch update norm for batch size 256: 1.5e-3
Vezi că fiecare actualizare pe loturi este mai mică atunci când dimensiunea lotului este mai mare. De ce s-ar întâmpla acest lucru?
Pentru a înțelege acest comportament, să creăm un scenariu fictiv, în care avem doi vectori de gradient a și b, fiecare reprezentând gradientul pentru un exemplu de instruire. Să ne gândim la modul în care dimensiunea medie de actualizare a lotului pentru dimensiunea lotului = 1 se compară cu cea a lotului = 2.

Dacă folosim o mărime a lotului de unu, vom face un pas în direcția a, apoi b, ajungând la punctul reprezentat de a+b. (Din punct de vedere tehnic, gradientul pentru b ar fi recalculat după aplicarea lui a, dar să ignorăm acest lucru deocamdată). Rezultă o dimensiune medie de actualizare a lotului de (|a|+|b|)/2 – suma dimensiunilor de actualizare a lotului, împărțită la numărul de actualizări ale lotului.
Dar, dacă folosim o dimensiune a lotului de doi, actualizarea lotului este în schimb reprezentată de vectorul (a+b)/2 – săgeata roșie din figura 12. Astfel, dimensiunea medie de actualizare a lotului este |(a+b)/2| / 1 = |a+b|/2.
Acum, să comparăm cele două dimensiuni medii de actualizare a lotului:

În ultimul rând, am folosit inegalitatea triunghiulară pentru a arăta că mărimea medie de actualizare a lotului pentru mărimea lotului 1 este întotdeauna mai mare sau egală cu cea a lotului de mărimea 2.
După cumva, pentru ca mărimea medie a lotului pentru mărimea lotului 1 și mărimea lotului 2 să fie egală, vectorii a și b trebuie să fie îndreptați în aceeași direcție, deoarece atunci |a| + |b| = |a+b|. Putem extinde acest argument la n vectori – numai atunci când toți cei n vectori sunt îndreptați în aceeași direcție, dimensiunile medii de actualizare a loturilor pentru mărimea lotului=1 și mărimea lotului=n sunt identice. Cu toate acestea, acest lucru nu se întâmplă aproape niciodată, deoarece este puțin probabil ca vectorii de gradient să fie orientați exact în aceeași direcție.

Dacă ne întoarcem la ecuația de actualizare a miniblocurilor din figura 16, spunem, într-un fel, că pe măsură ce creștem dimensiunea lotului |B_k|, mărimea sumei gradienților crește comparativ mai puțin rapid. Acest lucru se datorează faptului că vectorii de gradient sunt orientați în direcții diferite și, prin urmare, dublarea mărimii lotului (adică a numărului de vectori de gradient care trebuie însumați) nu dublează magnitudinea sumei de vectori de gradient rezultate. În același timp, împărțim la un numitor |B_k| care este de două ori mai mare, rezultând un pas de actualizare mai mic în general.
Acesta ar putea explica de ce actualizările loturilor pentru dimensiuni mai mari ale loturilor tind să fie mai mici – suma vectorilor de gradient devine mai mare, dar nu poate compensa complet numitorul mai mare|B_k|.
Ipoteza 2: Instruirea pe loturi mici găsește minimizatoare mai plate
Să măsurăm acum acuitatea ambelor minimizatoare și să evaluăm afirmația conform căreia instruirea pe loturi mici găsește minimizatoare mai plate. (Rețineți că această a doua ipoteză poate coexista cu prima – ele nu se exclud reciproc). Pentru a face acest lucru, împrumutăm două metode de la Keskar et al.
În prima, trasăm pierderea de instruire și de validare de-a lungul unei linii între un minimizator de lot mic (mărimea lotului 32) și un minimizator de lot mare (mărimea lotului 256). Această linie este descrisă de următoarea ecuație:

unde x_l* este minimizatorul lotului mare și x_s* este minimizatorul lotului mic, iar alpha este un coeficient între -1 și 2.

După cum putem vedea în grafic, minimizatorul lotului mic (alfa=0) este mult mai plat decât minimizatorul lotului mare (alfa=1), care variază mult mai brusc.
Rețineți că acesta este un mod destul de simplist de măsurare a ascuțimii, deoarece ia în considerare doar o singură direcție. Astfel, Keskar et al. propun o metrică de acuitate care măsoară cât de mult variază funcția de pierdere într-o vecinătate în jurul unui minimizator. În primul rând, definim vecinătatea după cum urmează:

unde epsilon este un parametru care definește dimensiunea vecinătății și x este minimizatorul (greutățile).
Apoi, definim metrica de acuitate ca fiind pierderea maximă în această vecinătate din jurul minimizatorului:

unde f este funcția de pierdere, iar intrările sunt ponderile.
Cu ajutorul definițiilor de mai sus, să calculăm ascuțimea minimizatorilor la diferite mărimi de lot, cu o valoare epsilon de 1e-3:
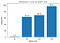
Aceasta arată că minimizoarele loturilor mari sunt într-adevăr mai clare, așa cum am văzut în graficul de interpolare.
În cele din urmă, să încercăm să reprezentăm grafic minimizoarele cu o vizualizare a pierderilor normalizate prin filtru, așa cum a fost formulată de Li et al . Acest tip de trasare alege două direcții aleatorii cu aceleași dimensiuni ca și ponderile modelului și apoi normalizează fiecare filtru convoluțional (sau neuron, în cazul straturilor FC) pentru a avea aceeași normă ca și filtrul corespunzător din ponderile modelului. Acest lucru asigură faptul că acuitatea unui minimizator nu este afectată de mărimile ponderilor sale. Apoi, se trasează pierderea de-a lungul acestor două direcții, centrul graficului fiind minimizatorul pe care dorim să îl caracterizăm.
.