Análisis de datos¶
Dado un conjunto de datos, se puede utilizar el método fit para estimar una transformada de blanqueo.
fit(Blanqueo, X; …)¶
Estima una transformada de blanqueo a partir de los datos dados en X. Aquí, X debe ser una matriz, cuyas columnas dan las muestras.
Esta función devuelve una instancia de Whitening.
Palabra clave Argumentos:
| nombre | descripción | por defecto |
|---|---|---|
| regcoef |
El coeficiente de regularización. La covarianza se regularizará de la siguiente manera cuando
|
zero(T) |
| mean |
El vector de la media, que puede ser cualquiera de:
|
nothing |
Nota: Esta función se basa internamente en cov_whiten para derivar la transformación W. La función cov_whiten en sí misma es también una función útil.
cov_whitening(C)¶
Derivar la matriz de coeficientes de la transformación de blanqueo W dada la matriz de covarianza C. Aquí, C puede ser una matriz cuadrada, o una instancia de Cholesky.
Internamente, esta función resuelve la transformada de blanqueo utilizando la factorización Cholesky. El razonamiento es el siguiente: dejemos que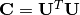 
y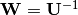 
, entonces 
.
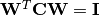Nota: La matriz de retorno W es una matriz triangular superior.
cov_whitening(C, regcoef)
Derivar una transformada de blanqueo basada en una covarianza regularizada, como C + (eigmax(C) * regcoef) * eye(d).
Además, el paquete también proporciona cov_whiten!, en el que la matriz de entrada C se sobrescribirá durante el cálculo. Esto puede ser más eficiente cuando C ya no se utiliza.
invsqrtm(C)¶
Computa inv(sqrtm(C)) a través de la descomposición simétrica de valores propios.