El primer gráfico muestra que los lotes de mayor tamaño recorren menos distancia por época. La distancia por época de entrenamiento del lote 32 varía entre 0,15 y 0,4, mientras que para el entrenamiento del lote 256 es de alrededor de 0,02-0,04. De hecho, como podemos ver en el segundo gráfico, la relación de las distancias de las épocas aumenta con el tiempo
¿Pero por qué el entrenamiento por lotes grandes recorre menos distancia por época? ¿Es porque tenemos menos lotes, y por tanto menos actualizaciones por época? ¿O es porque cada actualización de lote recorre menos distancia? O, ¿es la respuesta una combinación de ambas?
Para responder a esta pregunta, midamos el tamaño de cada actualización de lote.

Median batch update norm for batch size 32: 3.3e-3
Median batch update norm for batch size 256: 1.5e-3
Podemos ver que cada actualización de lote es más pequeña cuando el tamaño del lote es mayor. Para entender este comportamiento, establezcamos un escenario ficticio, en el que tenemos dos vectores de gradiente a y b, cada uno de los cuales representa el gradiente para un ejemplo de entrenamiento. Pensemos en cómo se compara el tamaño medio de actualización del lote para el tamaño del lote=1 con el del lote=2.

Si utilizamos un tamaño de lote de uno, daremos un paso en la dirección de a, luego b, terminando en el punto representado por a+b. (Técnicamente, el gradiente para b se volvería a calcular después de aplicar a, pero ignoremos eso por ahora). Esto resulta en un tamaño promedio de actualización por lotes de (|a|+|b|)/2 – la suma de los tamaños de actualización por lotes, dividida por el número de actualizaciones por lotes.
Sin embargo, si utilizamos un tamaño de lote de dos, la actualización por lotes está representada por el vector (a+b)/2 – la flecha roja en la Figura 12. Por lo tanto, el tamaño medio de actualización del lote es |(a+b)/2| / 1 = |a+b|/2.
Ahora, comparemos los dos tamaños medios de actualización del lote:

En la última línea, utilizamos la desigualdad del triángulo para demostrar que el tamaño medio de actualización del lote para el tamaño de lote 1 es siempre mayor o igual que el del tamaño de lote 2.
Por decirlo de otra manera, para que el tamaño medio de lote para el tamaño de lote 1 y el tamaño de lote 2 sea igual, los vectores a y b tienen que estar apuntando en la misma dirección, ya que es cuando |a| + |b| = |a+b|. Podemos extender este argumento a n vectores: sólo cuando todos los n vectores apuntan en la misma dirección, los tamaños medios de actualización del lote para el tamaño del lote=1 y el tamaño del lote=n son iguales. Sin embargo, este casi nunca es el caso, ya que es poco probable que los vectores del gradiente apunten exactamente en la misma dirección.

Si volvemos a la ecuación de actualización de minilotes de la Figura 16, en cierto sentido estamos diciendo que a medida que aumentamos el tamaño del lote |B_k|, la magnitud de la suma de los gradientes aumenta comparativamente menos rápido. Esto se debe al hecho de que los vectores gradientes apuntan en diferentes direcciones y, por lo tanto, duplicar el tamaño del lote (es decir, el número de vectores gradientes a sumar) no duplica la magnitud de la suma resultante de los vectores gradientes. Al mismo tiempo, estamos dividiendo por un denominador |B_k| que es el doble de grande, lo que resulta en un paso de actualización más pequeño en general.
Esto podría explicar por qué las actualizaciones de lotes para tamaños de lotes más grandes tienden a ser más pequeñas – la suma de vectores de gradiente se hace más grande, pero no puede compensar completamente el denominador más grande|B_k|.
Hipótesis 2: El entrenamiento por lotes pequeños encuentra minimizadores más planos
Midamos ahora la nitidez de ambos minimizadores, y evaluemos la afirmación de que el entrenamiento por lotes pequeños encuentra minimizadores más planos. (Nótese que esta segunda hipótesis puede coexistir con la primera, no son mutuamente excluyentes). Para ello, tomamos prestados dos métodos de Keskar et al.
En el primero, trazamos la pérdida de entrenamiento y validación a lo largo de una línea entre un minimizador de lote pequeño (tamaño de lote 32) y un minimizador de lote grande (tamaño de lote 256). Esta línea se describe mediante la siguiente ecuación:

donde x_l* es el minimizador de lotes grandes y x_s* es el minimizador de lotes pequeños, y alfa es un coeficiente entre -1 y 2.

Como podemos ver en el gráfico, el minimizador de lotes pequeños (alfa=0) es mucho más plano que el minimizador de lotes grandes (alfa=1), que varía de forma mucho más brusca.
Nótese que ésta es una forma bastante simplista de medir la nitidez, ya que sólo considera una dirección. Así, Keskar et al proponen una métrica de agudeza que mide cuánto varía la función de pérdida en una vecindad alrededor de un minimizador. En primer lugar, definimos la vecindad como sigue:

donde epsilon es un parámetro que define el tamaño de la vecindad y x es el minimizador (los pesos).
Entonces, definimos la métrica de agudeza como la pérdida máxima en esta vecindad alrededor del minimizador:

donde f es la función de pérdida, siendo las entradas los pesos.
Con las definiciones anteriores, calculemos la nitidez de los minimizadores en varios tamaños de lote, con un valor epsilon de 1e-3:
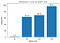
Esto muestra que los minimizadores de lotes grandes son efectivamente más nítidos, como vimos en el gráfico de interpolación.
Por último, probemos a trazar los minimizadores con una visualización de pérdida normalizada por filtro, tal y como formulan Li et al . Este tipo de gráfico elige dos direcciones aleatorias con las mismas dimensiones que los pesos del modelo, y luego normaliza cada filtro convolucional (o neurona, en el caso de las capas FC) para que tenga la misma norma que el filtro correspondiente en los pesos del modelo. Esto garantiza que la nitidez de un minimizador no se vea afectada por las magnitudes de sus pesos. A continuación, traza la pérdida a lo largo de estas dos direcciones, siendo el centro del gráfico el minimizador que deseamos caracterizar.