Un gráfico de control es un mecanismo para entender el comportamiento del proceso, la previsibilidad y la estabilidad en el tiempo. Sabemos que cualquier proceso tiene una cierta cantidad de variabilidad natural. Pero, ¿cómo podemos saber si la variabilidad del proceso se ha «descontrolado»?
Un gráfico de control es una herramienta utilizada en el «Control de Calidad» para inferir que se ha producido un cambio no planificado en un proceso. Una variable continua del proceso X lo mide. Ejemplo de variable de proceso podría ser, pero no se limita a, como –
- el tiempo de espera en un restaurante de comida rápida o en el mostrador de facturación de un aeropuerto,
- la varianza de la programación y los costes a lo largo de las iteraciones,
- el volumen y la frecuencia de los cambios de alcance a lo largo de las iteraciones,
Normalmente desarrollamos gráficos de control para procesos –
- que son repetitivos para producir lotes fabricados, y
- las expectativas se establecen para actuar en torno a la variable continua del proceso X.
Un proceso repetitivo es aquel en el que el proceso hace lo mismo de la misma manera y produce los mismos resultados.
Según la Guía del PMBOK® Gráfico de control es :-
Una representación visual de los datos a lo largo del tiempo y frente a los límites de mando establecidos, que tiene una línea central que ayuda a detectar una tendencia de los valores trazados hacia cualquiera de los límites de control
Un gráfico de control tiene los siguientes componentes:
- Línea central: En el gráfico de control mostramos la línea central como capacidad ideal deseada de un proceso. Es una representación gráfica de la variable continua del proceso X . La línea central es la media calculada de los puntos de datos. Estos puntos de datos son la salida repetitiva del proceso con el tiempo.
- Límite de especificación: Establecemos los límites de especificación normalmente después de analizar las expectativas del cliente. A veces mencionamos estos límites en los acuerdos. Puede haber penalizaciones asociadas si los puntos de datos exceden el límite de especificación.
- Límites de control: Establecemos límites de control superiores e inferiores para los gráficos de control. Diseñamos estos límites utilizando análisis estadísticos o a partir de registros históricos. Graficamos los puntos de datos de un proceso para realizar un análisis de tendencia hacia cualquiera de los límites de control y con respecto a la línea central.
Para procesos repetitivos, los límites de control se establecen generalmente en +_ 3 sigma alrededor de un proceso. Variable X o media del proceso, es decir, la línea central. El límite de control superior se traza a 3 desviaciones estándar por encima de la media del proceso, y el control inferior se traza a 3 desviaciones estándar por debajo de la línea central, o media del proceso.
Establecemos estos límites para predecir si el proceso necesita una acción correctiva para adecuar el rendimiento del proceso a la estabilidad y capacidad necesarias. El análisis de los puntos de datos con la línea central y los límites de control nos ayudan a prevenir un rendimiento del proceso no natural con el tiempo. Los límites de control son más estrictos que los límites de especificación. Así podemos tomar acciones correctivas antes de que los puntos de datos empiecen a alcanzar el límite de especificación.
Representación gráfica de los componentes del gráfico de control: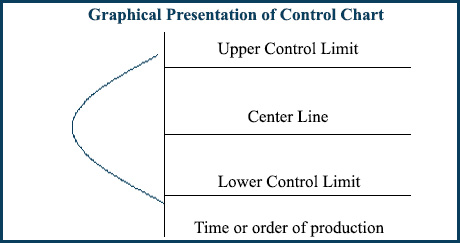
Cómo determinar si el proceso está «En control» o «Fuera de control»:
Tomamos muestras de puntos de datos como salida del proceso y las trazamos sobre el gráfico de control. Y, a continuación, realizamos un análisis sobre cómo podemos presentar estos datos con respecto a la –
Línea central y al límite de control superior &inferior. El énfasis es entender si los puntos de datos están dentro de los límites aceptables.
Los puntos de datos dentro de +- 3 sigma están «en Control», y dentro de los límites aceptables excluyendo la regla de siete (descrita más adelante). Los puntos de datos están dentro de +-3 sigma significa que estos puntos de datos no están cruzando ninguno de los límites de control. Cualquier cosa más allá del límite de control requiere una investigación.
Ahora, venga a la – ¿Qué es la regla de siete en la gestión de proyectos?
Cuando siete puntos de datos consecutivos vienen a cada lado de la media –
Entonces tomamos este proceso Fuera de Control basado en la heurística de la Regla de Siete.
En este caso, aunque los puntos de datos no están cruzando los límites de control, pero como el proceso repetitivo no está generando una salida aleatoria –
Esto puede ser señal de un problema en un proceso. Se hacen esfuerzos para entender la situación y la raíz del problema del proceso.
En resumen, se considera que el proceso está fuera de control –
- Cuando los puntos de datos están fuera de los límites de control superior o inferior y/o
- Se trazan siete puntos consecutivos a ambos lados de la media, es decir, la línea central.
Necesitamos investigar ambas causas especiales de varianza.
Desarrollo del gráfico de control:
Como mencioné anteriormente, los gráficos de control se utilizan para mostrar si un proceso repetitivo está –
- «en control» o
- «fuera de control».
Estoy tomando un ejemplo de un proceso para probar las construcciones semanales repetitivas. En un viernes promedio EOD, tenemos que terminar la construcción semanal. Ahora tenemos que entender el rango aceptable. Las observaciones indican que a veces nos retrasamos 1 o 2 días y que algún día la compilación se adelanta un día.
El propietario del proceso puede aceptar la compilación con un día de retraso o de adelanto. Pero, ¿cómo podemos decir matemáticamente que –
- Una variación aceptable sería un día o dos días? Y
- Si alguna semana las construcciones se terminan en un punto, donde se identifica la necesidad de una acción correctiva.
El gráfico de control se utiliza para entender la identificación matemática de los límites de control y la necesidad de una acción correctiva.
Supongamos que hemos recogido 30 semanas de datos para entender si la salida del proceso está dentro de los límites aceptables.
Ahora tenemos que calcular el promedio de deslizamiento en la construcción de 30 semanas: Promedio de deslizamiento de los puntos de datos en días, es decir, 0,73 días.
Ahora se calcula la desviación estándar. La desviación estándar significa cuánta variación respecto a la media: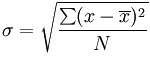
σ = la desviación estándar
x = cada valor de la población
x̄ = la media de los valores
N = el número de valores
Usando la fórmula anterior la desviación estándar será 5,132273364.
Para obtener los límites de control, tenemos que multiplicar la desviación estándar por 3. En este caso, el valor de tres sigmas será 15,39682009.
Ahora es el momento de calcular el límite de control superior e inferior:
El límite de control superior será la suma de 3 sigmas y el deslizamiento medio en semanas, es decir, la suma de 15,39682009 y 0,73. Como resultado obtendremos 16,13 como límite de control superior.
El límite de control inferior será la sustracción de 3 Sigma del deslizamiento medio en semanas, es decir, la sustracción de 15,39682009 de 0,73. Como resultado obtendremos -14,66 como límite de control inferior.
Como resumen:
Aquí 3 Sigma es igual a 15,39682009, la media de deslizamiento en días es 0,73 días, el límite de control superior es 16,13, y el límite de control inferior es -14.66.
Ahora, finalmente, se puede desarrollar un gráfico de control utilizando un gráfico de líneas 2D: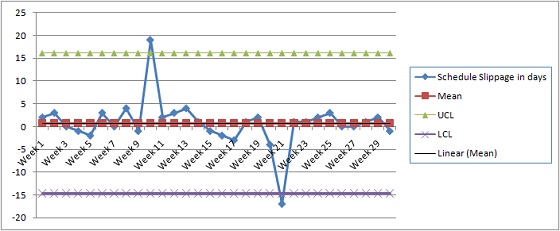
Gráfico de control (x) utilizando los límites de control media + 3 sigma y media – 3 sigma
Ahora tenemos que analizar los gráficos. Hay dos puntos de datos (dos semanas), que están más allá de los límites de control y eso es lo que tenemos que hacer la investigación más. Como mencioné anteriormente, el límite de control nos ayuda a determinar si es necesario tomar medidas correctivas o no. Cuando los puntos de datos están más allá del límite de control, muestra que la variabilidad no es natural.
El análisis de la desviación estándar y del gráfico de control indica –
Tenemos una variación pobre. Aquí, tenemos que investigar la raíz del problema. Y, podemos utilizar otras herramientas como el diagrama «Causa y Efecto», «Análisis de Pareto» para el mismo. Tras el análisis de la causa raíz y la adopción de medidas correctivas, podemos volver a dibujar el gráfico de control. Y, averiguar si la variación se está reduciendo con el tiempo.
Un punto crucial es que como tenemos que eliminar la causa especial es decir, dos semanas. Podemos elegir una herramienta de lluvia de ideas para entender –
Qué eventos celebrados durante esas dos semanas contribuyen a la variación de la causa especial. En ágil, podemos hacer esto en la retrospectiva de la iteración. En este caso, el objetivo de la iteración, la retrospectiva sería determinar qué podemos hacer para poner el proceso de pruebas bajo control.
¿Para qué se utiliza un gráfico de control?
El gráfico de control se utiliza en el «Plan de Calidad» para entender –
¿Qué se necesita para asegurarse de que los procesos repetitivos producirán resultados dentro de los límites aceptables?
Diseñamos el plan de mejora del proceso en consecuencia.
Las políticas de calidad se refinan para obtener el resultado deseado. Y, se definen las métricas para medir el rendimiento del proceso. Los registros históricos de los gráficos de control juegan un papel importante en el desarrollo del –
- plan de mejora del proceso,
- plan de gestión de la calidad, y
- métricas de la calidad.
También, utilizamos el Gráfico de Control como herramienta y técnica durante el «Control de la Calidad» para entender –
si el proceso repetitivo produce resultados dentro de un rango aceptable y de forma aleatoria.
Si no es así, entonces es necesario realizar una investigación para eliminar la variación por causa especial.
En resumen, el gráfico de control es una herramienta útil para entender si un proceso es estable con el tiempo y produce resultados dentro de los límites aceptables y de forma aleatoria.
Espero que este blog haya respondido suficientemente a todas sus dudas relacionadas con el Gráfico de Control. Buena suerte con su examen de certificación PMP®.
Puede unirse a la discusión sobre el mismo en nuestro Foro. También puede entrar en nuestro canal de YouTube para ver el vídeo sobre el mismo.
Inscríbase en nuestro Programa de Introducción a la Certificación PMP® GRATIS para aprender más sobre la certificación PMP®