Persentiili on paikka jakaumassa, jonka ”alapuolella” (vasemmalla puolella) on tietty määrä (tai prosenttiosuus) jakaumasta. Toisin sanoen, jos #n^”th ”# persentiili on #x#, ja arvomme jakaumasta satunnaisluvun #X#, niin todennäköisyys sille, että #X# on pienempi kuin #x#, on #n %#:
#n^”th” ” persentiili” = x” ”#keskiarvo#” ” P(X < x)=n%.#
Esimerkiksi tavallisessa normaalikäyrässä (jossa #mu = 0# ja #sigma = 1#) piste, jossa #x=0# (ts. #y#-akseli) on 50. persentiili, koska 50 % käyrän pinta-alasta osuu #x=0#:n vasemmalle puolelle:

Standardinormaalijakauma #Z# on niin hyvä lähtökohta, että meillä on itse asiassa arvotaulukko, joka on suunniteltu nimenomaan tämän käyrän persentiilien etsimistä varten. Sitä kutsutaan #z#-taulukoksi, ja se näyttää jotakuinkin tältä:
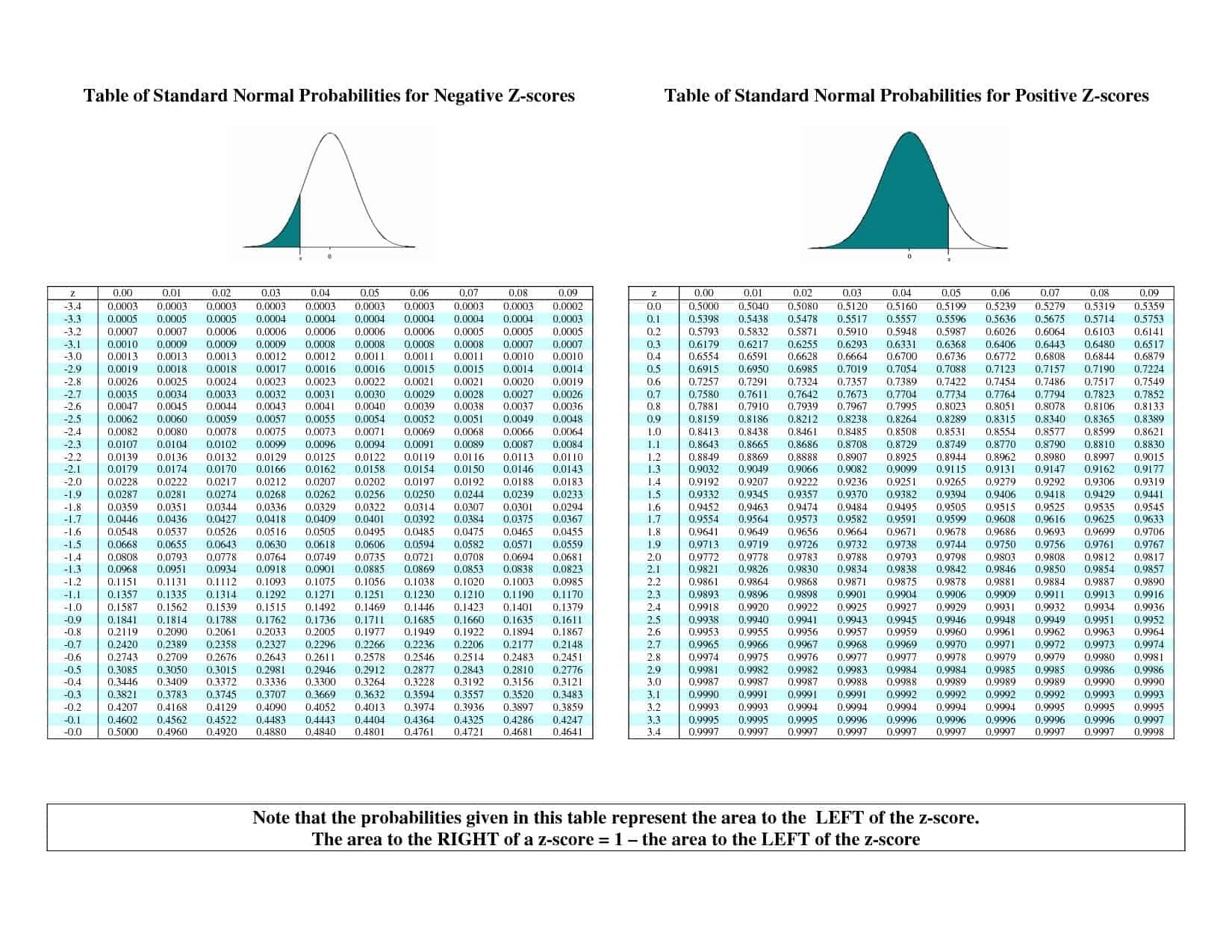
Miten sitä käytetään? Sanotaan, että haluamme tavallisen normaalijakauman 25. prosenttipisteen. Etsimme taulukosta arvoa 0,25 lähinnä olevan arvon (joka sattuu olemaan 0,2514) ja näemme, että se on rivillä #”-”0,6# ja sarakkeessa #0,07#. Tämän taulukon osalta tämä tarkoittaa, että 25. persentiili on (suunnilleen) #”-”0.67#.
Mutta hetkinen – miten tämä auttaa, kun haluamme persentiilin mille tahansa normaalijakaumalle #X#? Meidän on löydettävä yhteys minkä tahansa käyrän ja normaalin normaalikäyrän välille. Tämä yhteys löydetään siirtämällä jakaumaa #X# vasemmalta oikealle niin, että sen keskipiste on #0#, ja sitten venyttämällä/karsimalla sitä niin, että sen keskihajonta on #1#. Kaava tälle on:
#Z=(X-mu)/sigma#
missä #mu# on #X#:n keskiarvo ja #sigma# on #X#:n s.d..
Jos tiedämme haluamamme prosenttiluvun jakaumasta #Z#, voimme ratkaista #X#:n järjestämällä yhtälön uudelleen muotoon
#X=sigma Z + mu#.
Käytetään esimerkkinä ensimmäistä kysymystäsi, jossa #X# on normaalijakautunut siten, että #mu = 81,2# ja #sigma = 12,4#, ja etsimme 16. persentiiliä.
Yllä olevasta taulukosta voidaan päätellä, että 16. persentiili #Z#-jakaumasta on noin #”-”0,99#. Vastaava paikka #X#-jakaumassamme on siis:
#X=(12.4)(”-”0.99)+81.2#
#color(white)X=”-”12.276+81.2#
#color(white)X=68.924#
Tämä kertoo seuraavaa: jos #X# on normaalikäyrä, jonka #mu=81.2 ” jalkaa ”# ja #sigma = 12.4 ” jalkaa ”#, niin on 16% todennäköisyys, että havainto #X#:stä on pienempi kuin #68.924 ” jalkaa ”#.
Loppuosa jätän sinulle harjoitustehtäväksi; yllä olevilla kaavoilla sen ei pitäisi olla kovin vaikeaa.
Toivottavasti tämä auttaa!