Commander STATA
Modèles à commutation de Markov
Les points forts
- Modélisation à transition de Markov.transition de Markov
- Modèle autorégressif
- Modèle de régression dynamique
- Paramètres de régression dépendant de l’état
- Paramètres de variance dépendant de l’état
- .paramètres de variance dépendants de l’état
- Tableaux de
- Probabilités de transition
- Durées d’état attendues
- Prédictions
- Valeurs attendues de la variable dépendante
- Probabilités d’être dans un état
- Statique (à uneétape)
- Dynamique (multi-étapes)
- RMSE des prédictions
De quoi s’agit-il ?
Parfois, les processus évoluent dans le temps avec des changements discrets dans les résultats.
Pensez aux récessions et aux expansions économiques. Au début d’une récession, la production et l’emploi chutent et restent faibles, puis, plus tard, la production et l’emploi augmentent. Pensez aux troubles bipolaires dans lesquels il y a des périodes maniaques suivies de périodes dépressives, et le processus se répète. Statistiquement, les moyennes, les variances et d’autres paramètres changent d’un épisode à l’autre (régimes). Notre problème est d’estimer quand les régimes changent et les valeurs des paramètres associés à chaque régime. Demander quand les régimes changent est équivalent à demander combien de temps les régimes persistent.
Dans les modèles à transition de Markov, en plus d’estimer les moyennes, les variances, etc. de chaque régime, nous estimons également la probabilité de changement de régime. Les probabilités de transition estimées pour un certain problème pourraient être, les suivantes :
| de/à | ||
| état | . 1 2 | |
| 1 | 0.82 0,18 | |
| 2 | 0,75 0,25 | |
Commence dans l’état 1. La probabilité de passer de l’état 1 à l’état 1 est de 0,82. Dit autrement, une fois dans l’état 1, le processus a tendance à y rester. Cependant, avec une probabilité de 0,18, le processus transite vers l’état 2. L’état 2 n’est pas aussi persistant. Avec une probabilité de 0,75, les processus reviennent de l’état 2 à l’état 1 dans la période de temps suivante.
Les modèles de Markov-switching ne sont pas limités à deux régimes, bien que les modèles à deux régimes soient courants.
Dans l’exemple ci-dessus, nous avons décrit la commutation comme étant abrupte ; la probabilité a changé instantanément. De tels modèles de Markov sont appelés des modèles dynamiques. Les modèles de Markov peuvent également tenir compte de changements plus lisses en modélisant les probabilités de transition comme un processus autorégressif.
Ainsi, la commutation peut être lisse ou abrupte.
Voyons comment cela fonctionne
Regardons les changements de moyenne entre les régimes. En particulier, nous allons analyser le taux des fonds fédéraux. Le taux des fonds fédéraux est le taux d’intérêt que la banque centrale des États-Unis impose aux banques commerciales pour les prêts au jour le jour. Nous allons examiner les variations du taux des fonds fédéraux de 1954 à la fin de 2010. Voici les données :
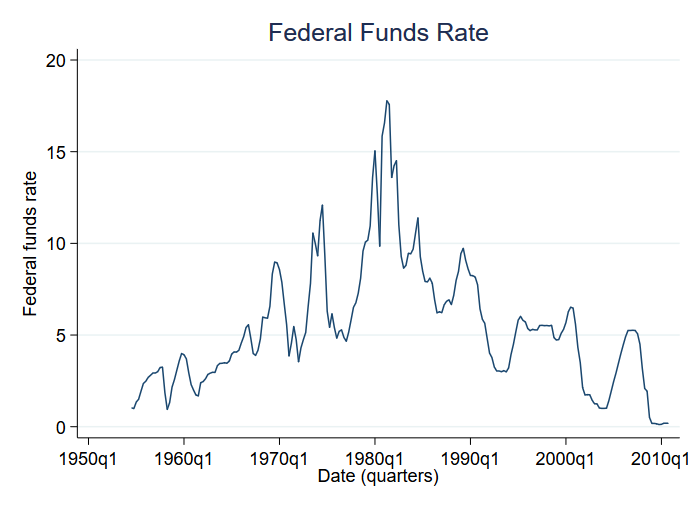
Nous avons des données trimestrielles. Les taux d’intérêt élevés semblent caractériser les années 70 et 80. Nous supposerons qu’il existe un autre régime de taux d’intérêt plus faibles qui semblent caractériser les autres décennies.
Pour ajuster un modèle à commutation dynamique (changement brusque) avec deux régimes, nous tapons
. mswitch dr fedfundsPerforming EM optimizaton:Performing gradient-based optimization:
| Itération 0: | log-vraisemblance = -508.66031 |
| Itération 1: | log-vraisemblance = -508.6382 |
| Itération 2: | log-vraisemblance = -508.63592 |
| Itération 3: | log-vraisemblance = -508.63592 |
Régression dynamique à commutation de MarkovÉchantillon : 1954q3 – 2010q4 Nbre d’obs. d’obs = 226Nombre d’états = 2 AIC = 4,5455Probabilités inconditionnelles : transition HQIC = 4,5760 SBIC = 4,6211Log likelihood = -508.63592
| fedfunds | Coef. Std. Err. z P>|z| | |
| State1 | ||
| _cons | 3.70877 .1767083 20.99 0.000 3.362428 4.055112 | |
| State2 | ||
| _cons | 9.556793 .2999889 31.86 0.000 8.968826 10.14476 | |
| sigma | 2.107562 .1008692 1.918851 2.314831 | |
| p11 | .9820939 .0104002 .9450805 .9943119 | |
| p21 | .0503587 .0268434 .0173432 .1374344 | |
La sortie ci-dessus indique
- les moyennes des deux états (_cons);
- un seul écart-type pour l’ensemble du processus (sigma) ; et
- les probabilités de transition de l’état 1 à 1 et de l’état 2 à 1 (p11 et p21).
L’état1 est l’état à taux modéré (moyenne de 3,71%).
L’état2 est l’état à taux élevé (moyenne de 9,56%).
| de/à | ||
| état | . 1 2 | |
| 1 | 0.98 1 – 0,98 | |
| 2 | 0,05 1 – 0,05 | |
Les deux états sont incroyablement persistants (probabilités 1->1 et 2->2 de 0,98 et 0,95).
Parmi les choses que l’on peut prédire après estimation, il y a la probabilité d’être dans les différents états. Nous n’avons que deux états, et donc la probabilité d’être dans (disons) l’état 2 nous indique la probabilité pour les deux états. Nous pouvons obtenir la probabilité prédite et la représenter graphiquement avec les données originales :
. predict prfed, pr
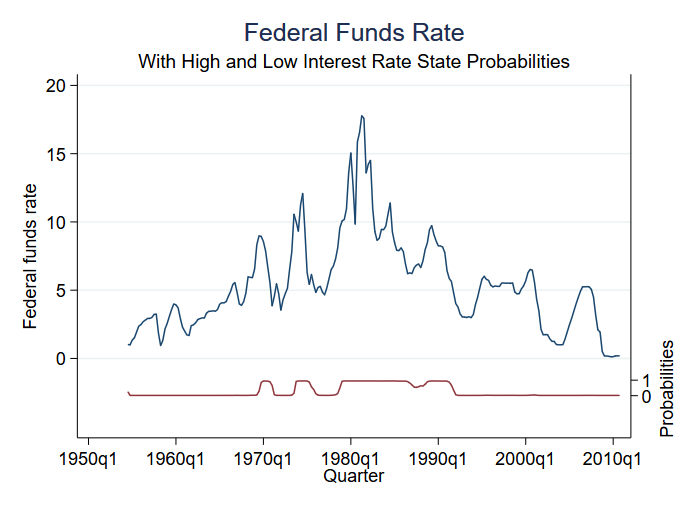
Le modèle présente une faible incertitude quant au régime à chaque instant. On observe trois périodes d’états à taux élevé et quatre périodes d’états à taux modéré.
Voyons comment cela fonctionne
Prenons un exemple d’épidémie de maladie, à savoir les oreillons pour 10 000 résidents à New York entre 1929 et 1972. On pourrait penser que les épidémies correspondent à des changements de moyenne, mais ce que nous voyons dans les données est un changement encore plus important de la variance :
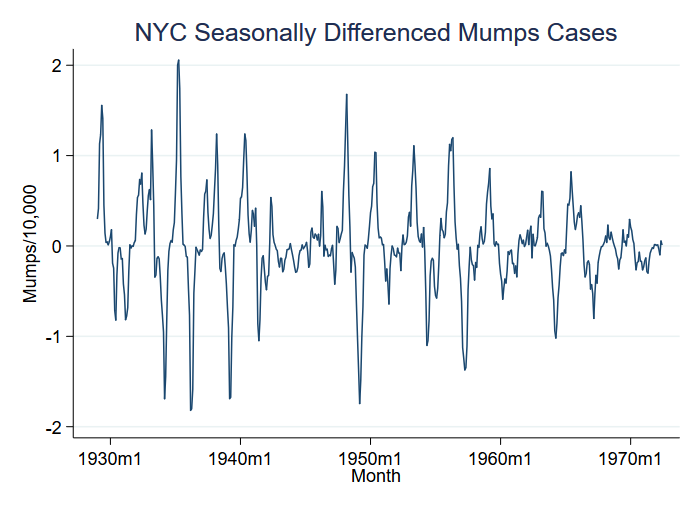
Nous avons représenté graphiquement la variable S12.mumpspc, c’est-à-dire les cas d’oreillons par habitant en différence saisonnière sur une période de 12 mois, et nous allons analyser S12.mumpspc.
Nous allons supposer deux régimes dans lesquels la moyenne et la variance de S12.mumpspc changent. Pour ajuster un modèle dynamique (changement brusque), nous tapons
. mswitch dr S12.mumpspc, varswitch switch(LS12.mumpspc, noconstant)Performing EM optimizaton:Performing gradient-based optimization:
| Itération 0: | log vraisemblance = 110,9372 (non concave) |
| Itération 1: | log vraisemblance = 120.68028 |
| Itération 2: | Vraisemblance logarithmique = 123,23244 |
| Itération 3: | Vraisemblance logarithmique = 131,47084 |
| Itération 3: | Vraisemblance logarithmique = 131.72182 |
| Itération 3: | Vraisemblance logarithmique = 131.7225 |
| Itération 3: | Vraisemblance logarithmique = 131.7225 |
Régression dynamique à commutation de MarkovEchantillon : 1929m2 – 1972m6 Nbre d’obs. d’obs = 521Nombre d’états = 2 AIC = -0.4826Probabilités inconditionnelles : transition HQIC = -0.4634 SBIC = -0.4336La vraisemblance logique = 131.7225
| S12.mumspc | Coef. Std. Err. z P>|z| | |
| State1 | ||
| mumpspc | ||
| LS12. | .4202751 .0167461 25.10 0.000 .3874533 .4530968 | |
| State2 | ||
| mumpspc | ||
| LS12. | .9847369 .0258383 38.11 0.000 .9340947 1.035379 | |
| sigma1 | .0562405 .0050954 .0470901 .067169 | |
| sigma2 | .2611362 .0111191 .2402278 .2838644 | |
| p11 | .762733 .0362619 .6846007 .8264175 | |
| p12 | .1473767 .0257599 .1036675 .205294 | |
Sont rapportées
- les moyennes des deux états de S12.mumpspc (0,42 et 0,98);
- les écarts types des deux états (0,06 et 0,26) ; et
- les probabilités de transition de l’état 1 à 1 et de l’état 2 à 1 (0,76 et 0,15).
L’état 1 est l’état à faible variance.
L’ensemble complet des probabilités de transition est le suivant :