Analyse des données¶
Donné un ensemble de données, on peut utiliser la méthode fit pour estimer une transformée de blanchiment.
fit(Blanchiment, X ; …)¶
Estime une transformée de blanchiment à partir des données données données dans X. Ici, X doit être une matrice, dont les colonnes donnent les échantillons.
Cette fonction renvoie une instance de Whitening.
Arguments de mots clés:
| nom | description | défaut |
|---|---|---|
| regcoef |
Le coefficient de régularisation. La covariance sera régularisée de la manière suivante lorsque
|
zero(T) |
| mean |
Le vecteur moyen, qui peut être l’un ou l’autre:
|
nothing |
Note : Cette fonction s’appuie en interne sur cov_whiten pour dériver la transformation W. La fonction cov_whiten elle-même est également une fonction utile.
cov_whitening(C)¶
Dériver la matrice de coefficient de transformation de blanchiment W étant donné la matrice de covariance C. Ici, C peut être soit une matrice carrée, soit une instance de Cholesky.
Internellement, cette fonction résout la transformée de blanchiment en utilisant la factorisation de Cholesky. Le raisonnement est le suivant : laissons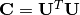 
et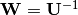 
, alors 
.
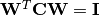Note : La matrice de retour W est une matrice triangulaire supérieure.
cov_whitening(C, regcoef)
Dériver une transformée de blanchiment basée sur une covariance régularisée, comme C + (eigmax(C) * regcoef) * eye(d).
En outre, le paquet fournit également cov_whiten!, dans lequel la matrice d’entrée C sera écrasée pendant le calcul. Cela peut être plus efficace lorsque C n’est plus utilisé.
invsqrtm(C)¶
Calculer inv(sqrtm(C)) par décomposition symétrique des valeurs propres.