Le premier graphique ci-dessus montre que les lots de taille plus importante parcourent effectivement moins de distance par époque. La distance par époque de formation du lot 32 varie de 0,15 à 0,4, tandis que pour la formation du lot 256, elle se situe autour de 0,02-0,04. En fait, comme nous pouvons le voir dans le second graphique, le rapport des distances d’époques augmente avec le temps !
Mais pourquoi l’entraînement par lots importants parcourt-il moins de distance par épochée ? Est-ce parce que nous avons moins de lots, et donc moins de mises à jour par époque ? Ou est-ce parce que chaque mise à jour par lot parcourt moins de distance ? Ou, la réponse est-elle une combinaison des deux ?
Pour répondre à cette question, mesurons la taille de chaque mise à jour par lot.

Median batch update norm for batch size 32: 3.3e-3
Median batch update norm for batch size 256: 1.5e-3
Nous pouvons voir que chaque mise à jour par lot est plus petite lorsque la taille du lot est plus grande. Pourquoi serait-ce le cas ?
Pour comprendre ce comportement, mettons en place un scénario fictif, où nous avons deux vecteurs de gradient a et b, chacun représentant le gradient pour un exemple d’entraînement. Réfléchissons à la façon dont la taille moyenne de mise à jour du lot pour la taille de lot=1 se compare à celle de la taille de lot=2.

Si nous utilisons une taille de lot de un, nous ferons un pas dans la direction de a, puis de b, pour finir au point représenté par a+b. (Techniquement, le gradient pour b serait recalculé après avoir appliqué a, mais ignorons cela pour l’instant). Il en résulte une taille moyenne de mise à jour par lot de (|a|+|b|)/2 – la somme des tailles de mise à jour par lot, divisée par le nombre de mises à jour par lot.
Toutefois, si nous utilisons une taille de lot de deux, la mise à jour par lot est plutôt représentée par le vecteur (a+b)/2 – la flèche rouge de la figure 12. Ainsi, la taille moyenne de mise à jour du lot est |(a+b)/2| / 1 = |a+b|/2.
Maintenant, comparons les deux tailles moyennes de mise à jour du lot :

Dans la dernière ligne, nous avons utilisé l’inégalité triangulaire pour montrer que la taille moyenne de mise à jour des lots pour la taille de lot 1 est toujours supérieure ou égale à celle de la taille de lot 2.
En d’autres termes, pour que la taille moyenne des lots pour la taille de lot 1 et la taille de lot 2 soit égale, les vecteurs a et b doivent être orientés dans la même direction, puisque c’est quand |a| + |b| = |a+b|. Nous pouvons étendre cet argument à n vecteurs – ce n’est que lorsque tous les n vecteurs sont orientés dans la même direction que les tailles moyennes de mise à jour des lots pour la taille de lot 1 et la taille de lot n sont les mêmes. Cependant, ce n’est presque jamais le cas, car il est peu probable que les vecteurs de gradient pointent exactement dans la même direction.

Si nous revenons à l’équation de mise à jour des minis lots de la figure 16, nous disons en quelque sorte que lorsque nous augmentons la taille du lot |B_k|, la magnitude de la somme des gradients augmente comparativement moins rapidement. Cela est dû au fait que les vecteurs de gradient pointent dans des directions différentes, et donc que doubler la taille du lot (c’est-à-dire le nombre de vecteurs de gradient à additionner) ne double pas la magnitude de la somme des vecteurs de gradient résultante. Dans le même temps, nous divisons par un dénominateur |B_k| qui est deux fois plus grand, ce qui entraîne un pas de mise à jour plus petit dans l’ensemble.
Cela pourrait expliquer pourquoi les mises à jour de lots pour les tailles de lots plus grandes ont tendance à être plus petites – la somme des vecteurs de gradient devient plus grande, mais ne peut pas compenser entièrement le dénominateur|B_k| plus grand.
Hypothèse 2 : L’entraînement par petits lots trouve des minimiseurs plus plats
Mesurons maintenant la netteté des deux minimiseurs, et évaluons l’affirmation selon laquelle l’entraînement par petits lots trouve des minimiseurs plus plats. (Notez que cette deuxième hypothèse peut coexister avec la première – elles ne sont pas mutuellement exclusives). Pour ce faire, nous empruntons deux méthodes à Keskar et al.
Dans la première, nous traçons la perte de formation et de validation le long d’une ligne entre un petit minimiseur de lot (taille de lot 32) et un grand minimiseur de lot (taille de lot 256). Cette ligne est décrite par l’équation suivante :

où x_l* est le minimiseur à grand lot et x_s* est le minimiseur à petit lot, et alpha est un coefficient entre -1 et 2.

Comme on peut le voir sur le graphique, le petit minimiseur de lots (alpha=0) est beaucoup plus plat que le grand minimiseur de lots (alpha=1), qui varie beaucoup plus fortement.
Notez qu’il s’agit d’une façon assez simpliste de mesurer la netteté, puisqu’elle ne considère qu’une seule direction. Ainsi, Keskar et al proposent une métrique d’acuité qui mesure combien la fonction de perte varie dans un voisinage autour d’un minimiseur. Tout d’abord, nous définissons le voisinage comme suit :

où epsilon est un paramètre définissant la taille du voisinage et x est le minimiseur (les poids).
Puis, on définit la métrique de netteté comme la perte maximale dans ce voisinage autour du minimiseur :

où f est la fonction de perte, les entrées étant les poids.
Avec les définitions ci-dessus, calculons la netteté des minimiseurs à différentes tailles de lots, avec une valeur epsilon de 1e-3 :
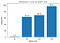
Ceci montre que les grands minimiseurs de lots sont effectivement plus nets, comme nous l’avons vu dans le graphe d’interpolation.
Enfin, essayons de tracer les minimiseurs avec une visualisation de la perte normalisée par filtre, comme formulé par Li et al . Ce type de tracé choisit deux directions aléatoires avec les mêmes dimensions que les poids du modèle, puis normalise chaque filtre convolutif (ou neurone, dans le cas des couches FC) pour avoir la même norme que le filtre correspondant dans les poids du modèle. Cela garantit que la netteté d’un minimiseur n’est pas affectée par l’amplitude de ses poids. Ensuite, il trace la perte le long de ces deux directions, le centre du tracé étant le minimiseur que nous souhaitons caractériser.