Un multiplexeur est un circuit combinatoire qui possède 2n lignes d’entrée et une seule ligne de sortie. Simplement, le multiplexeur est un circuit combinatoire à plusieurs entrées et une seule sortie. L’information binaire est reçue des lignes d’entrée et dirigée vers la ligne de sortie. Sur la base des valeurs des lignes de sélection, l’une de ces entrées de données sera connectée à la sortie.
Contrairement au codeur et au décodeur, il y a n lignes de sélection et 2n lignes d’entrée. Donc, il y a un total de 2N combinaisons possibles d’entrées. Un multiplexeur est également traité comme Mux.
Il existe différents types de multiplexeur qui sont les suivants :
Multiplexeur 2×1 :
Dans le multiplexeur 2×1, il n’y a que deux entrées, à savoir , A0 et A1, 1 ligne de sélection, c’est-à-dire S0 et des sorties uniques, c’est-à-dire Y. Sur la base de la combinaison des entrées qui sont présentes sur la ligne de sélection S0, l’une de ces 2 entrées sera connectée à la sortie. Le schéma bloc et la table de vérité du multiplexeur 2×1 sont donnés ci-dessous.
Schéma bloc:
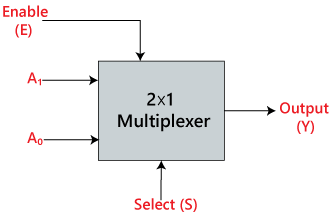
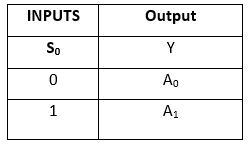
Table de vérité:
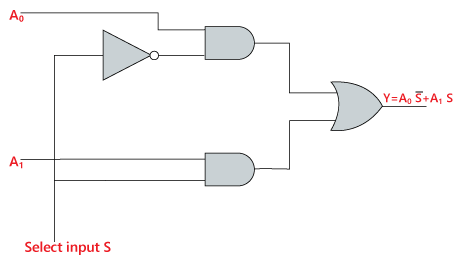
L’expression logique du terme Y est la suivante:
Y=S0′.A0+S0.A1
Le circuit logique de l’expression ci-dessus est donné ci-dessous:
Multiplexeur 4×1:
Dans le multiplexeur 4×1, il y a un total de quatre entrées, c’est-à-dire, A0, A1, A2 et A3, 2 lignes de sélection, c’est-à-dire, S0 et S1 et une seule sortie, c’est-à-dire, Y. Sur la base de la combinaison des entrées qui sont présentes sur les lignes de sélection S0 et S1, une de ces 4 entrées est connectée à la sortie. Le schéma bloc et la table de vérité du multiplexeur 4×1 sont donnés ci-dessous.
Schéma-bloc:
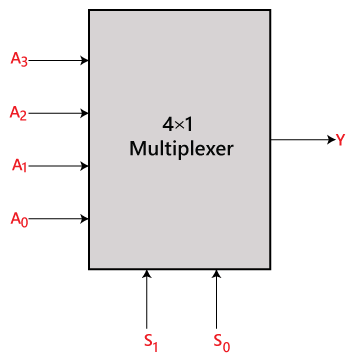
Table de vérité:
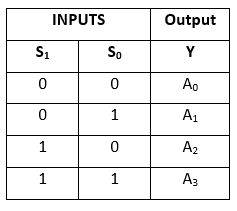
L’expression logique du terme Y est la suivante :
Y=S1′ S0′ A0+S1′ S0 A1+S1 S0′ A2+S1 S0 A3
Le circuit logique de l’expression ci-dessus est donné ci-dessous:
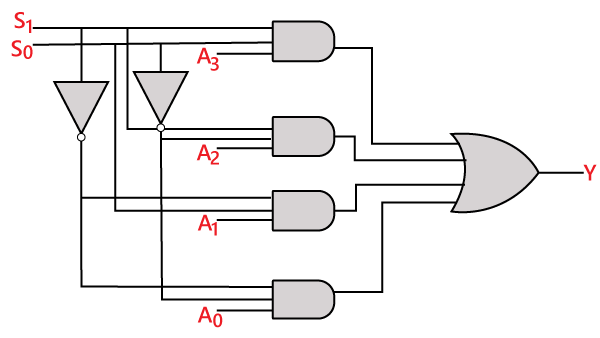
Multiplexeur 8 à 1
Dans le multiplexeur 8 à 1, il y a un total de huit entrées, c’est-à-dire.e., A0, A1, A2, A3, A4, A5, A6 et A7, 3 lignes de sélection, c’est-à-dire, S0, S1et S2 et une seule sortie, c’est-à-dire, Y. Sur la base de la combinaison des entrées qui sont présentes sur les lignes de sélection S0, S1 et S2, une de ces 8 entrées est connectée à la sortie. Le schéma bloc et la table de vérité du multiplexeur 8×1 sont donnés ci-dessous.
Schéma bloc:

Table de vérité:
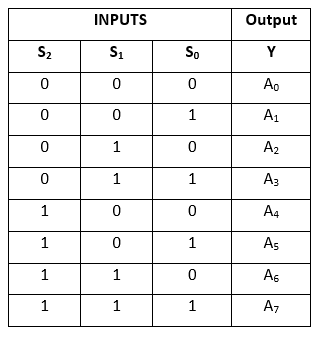
L’expression logique du terme Y est la suivante:
Y=S0′.S1′.S2′.A0+S0.S1′.S2′.A1+S0′.S1.S2′.A2+S0.S1.S2′.A3+S0′.S1′.S2 A4+S0.S1′.S2 A5+S0′.S1.S2 .A6+S0.S1.S3.A7
Le circuit logique de l’expression ci-dessus est donné ci-dessous :
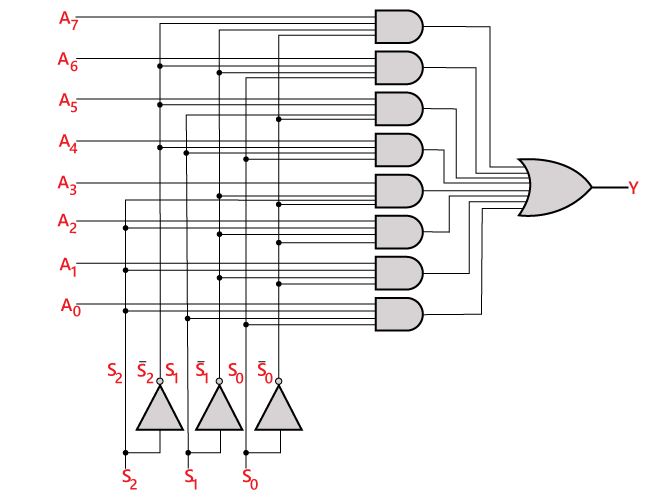
Multiplexeur 8×1 utilisant un multiplexeur 4×1 et 2×1
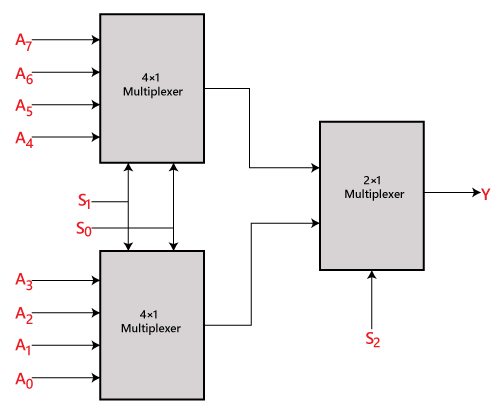
Nous pouvons mettre en œuvre le multiplexeur 8×1 en utilisant un multiplexeur d’ordre inférieur. Pour mettre en œuvre le multiplexeur 8×1, nous avons besoin de deux multiplexeurs 4×1 et d’un multiplexeur 2×1. Le multiplexeur 4×1 possède 2 lignes de sélection, 4 entrées et 1 sortie. Le multiplexeur 2×1 a seulement 1 ligne de sélection.
Pour obtenir 8 entrées de données, nous avons besoin de deux multiplexeurs 4×1. Le multiplexeur 4×1 produit une seule sortie. Donc, afin d’obtenir la sortie finale, nous avons besoin d’un multiplexeur 2×1. Le schéma fonctionnel du multiplexeur 8×1 utilisant le multiplexeur 4×1 et 2×1 est donné ci-dessous.
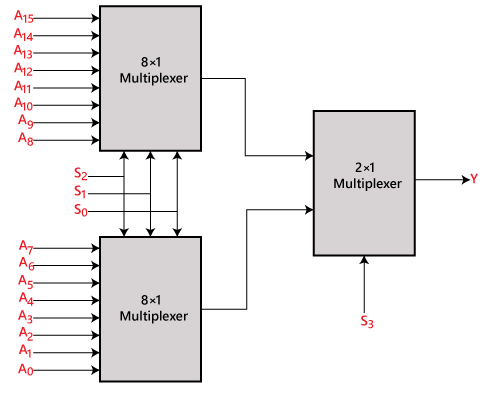
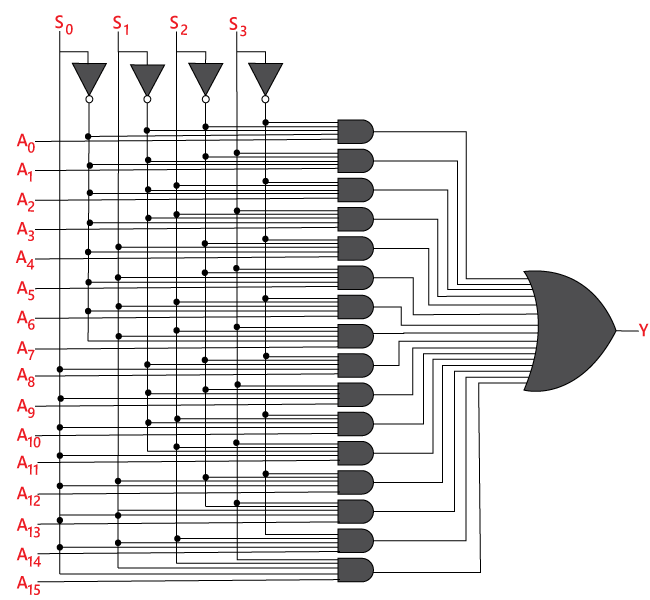
Multiplexeur 16 à 1
Dans le multiplexeur 16 à 1, il y a un total de 16 entrées, c’est-à-dire A0, A1, …, A16, 4 lignes de sélection, c’est-à-dire, S0, S1, S2, et S3 et une seule sortie, c’est-à-dire Y. Sur la base de la combinaison des entrées qui sont présentes sur les lignes de sélection S0, S1, et S2, l’une de ces 16 entrées sera connectée à la sortie. Le schéma-bloc et la table de vérité du 16×1
Schéma-bloc:
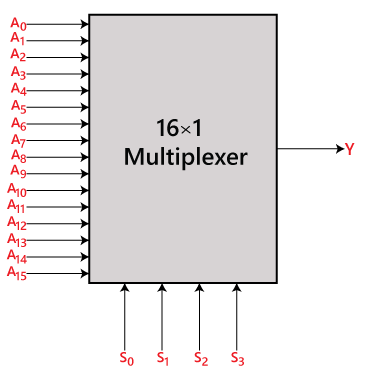
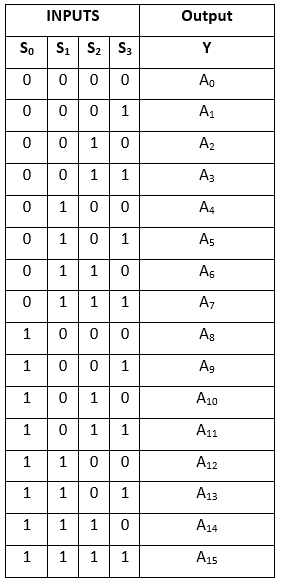
Table de vérité:
L’expression logique du terme Y est la suivante :
Le circuit logique de l’expression ci-dessus est donné ci-dessous:
Multiplexeur 16×1 utilisant un multiplexeur 8×1 et 2×1
Nous pouvons mettre en œuvre le multiplexeur 16×1 en utilisant un multiplexeur d’ordre inférieur. Pour mettre en œuvre le multiplexeur 8×1, nous avons besoin de deux multiplexeurs 8×1 et d’un multiplexeur 2×1. Le multiplexeur 8×1 possède 3 lignes de sélection, 4 entrées et 1 sortie. Le multiplexeur 2×1 a seulement 1 ligne de sélection.
Pour obtenir 16 entrées de données, nous avons besoin de deux multiplexeurs 8 ×1. Le multiplexeur 8×1 produit une seule sortie. Donc, afin d’obtenir la sortie finale, nous avons besoin d’un multiplexeur 2×1. Le schéma fonctionnel du multiplexeur 16×1 utilisant un multiplexeur 8×1 et 2×1 est donné ci-dessous.