A percentilis egy olyan hely az eloszlásban, amely az eloszlás egy meghatározott mennyiségét (vagy százalékát) “alatta” (tőle balra) tartalmazza. Más szóval, ha az #n^”th “# percentilis #x#, és kihúzunk egy véletlen számot #X# az eloszlásból, akkor annak az esélye, hogy #X# kisebb, mint #x#, #n %#:
#n^”th” ” percentilis” = x” “#közepes#” ” P(X < x)=n%.#
Egy standard normálgörbén (ahol #mu = 0# és #sigma = 1#) például az a pont, ahol #x=0# (azaz. az #y#-tengely) az 50. percentilis, mert a görbe területének 50%-a #x=0#-től balra esik:

A #Z# standard normális eloszlás olyan jó alapérték, hogy tulajdonképpen van egy értéktáblázatunk, amelyet kifejezetten e görbe percentiliseinek keresésére terveztek. Ezt #z#-táblázatnak hívják, és valahogy így néz ki:
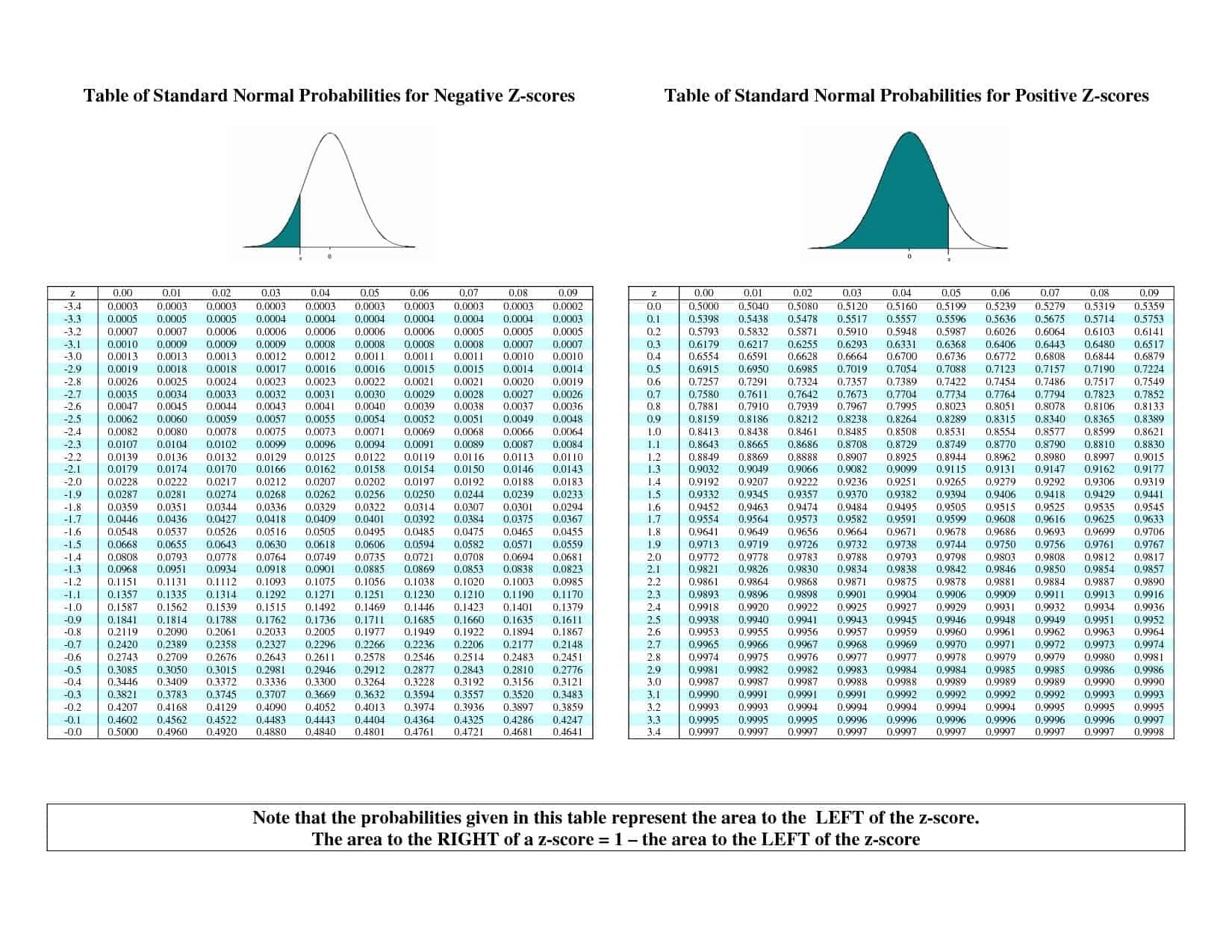
Hogyan használjuk? Tegyük fel, hogy a standard normális eloszlás 25. percentilisére vagyunk kíváncsiak. Megkeressük a táblázatban a 0,25-hez legközelebbi értéket (ami történetesen 0,2514), és látjuk, hogy ez a #”-“0,6# sorban és a #0,07# oszlopban található. A táblázat esetében ez azt jelenti, hogy a 25. percentilis (megközelítőleg) #”-“0,67#.
De várjunk csak – hogyan segít ez, amikor bármelyik #X# normális eloszlás percentilisét akarjuk megadni? Meg kell találnunk a kapcsolatot bármelyik görbe és a standard normálgörbe között. Ezt a kapcsolatot úgy találjuk meg, hogy az #X# eloszlást balról jobbra eltoljuk úgy, hogy a középpontja #0# legyen, majd úgy nyújtjuk/nyújtjuk, hogy a szórása #1# legyen. Ennek a képlete:
#Z=(X-mu)/sigma#
ahol #mu# az #X# átlaga és #sigma# az #X# s.d. értéke.
Ha tudjuk, hogy a #Z# eloszlásból milyen percentilt szeretnénk, akkor az egyenlet átrendezésével megoldhatjuk #X# értékét úgy, hogy
#X=sigma Z + mu#.
Példaként használjuk az első kérdésedet, ahol #X# normális eloszlású #mu=81,2# és #sigma=12,4# értékkel, és a 16. percentilt keressük.
A fenti táblázatból a #Z# eloszlás 16. percentilise körülbelül #”-“0,99#. A mi #X# eloszlásunkban az ennek megfelelő hely tehát:
#X=(12.4)(“-“0.99)+81.2#
#color(white)X=”-“12.276+81.2#
#color(white)X=68.924#
Mit ez azt mondja: ha #X# egy normálgörbe #mu=81.2 ” láb “# és #sigma=12.4 ” láb “#, akkor 16% az esélye annak, hogy egy #X#-ből származó megfigyelés kisebb, mint #68.924 ” láb “#.
A többit meghagyom neked feladatnak; a fenti képletekkel nem lehet olyan nehéz.
Remélem, ez segít!