Multiplexer

A multiplexer egy kombinációs áramkör, amely 2n bemeneti és egy kimeneti vonallal rendelkezik. Egyszerűen a multiplexer egy több bemenetű és egy kimenetű kombinációs áramkör. A bináris információ a bemeneti vonalakról érkezik, és a kimeneti vonalra irányul. A kiválasztó vonalak értékei alapján az egyik adatbemenet a kimenethez csatlakozik.

A kódolótól és a dekódertől eltérően n kiválasztó vonal és 2n bemeneti vonal van. Tehát a bemeneteknek összesen 2N lehetséges kombinációja van. A multiplexert Mux-ként is kezelik.

A multiplexernek különböző típusai vannak, amelyek a következők:

2×1 multiplexer:

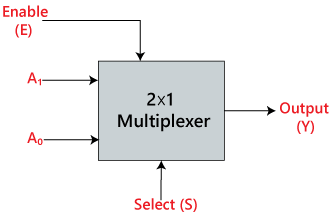
A 2×1 multiplexerben csak két bemenet van, azaz, A0 és A1, 1 választóvonal, azaz S0 és egyetlen kimenet, azaz Y. Az S0 választóvonalon lévő bemenetek kombinációja alapján a 2 bemenet közül az egyik a kimenethez csatlakozik. A 2×1 multiplexer blokkdiagramja és igazságtáblázata az alábbiakban látható.

Blokkdiagram:

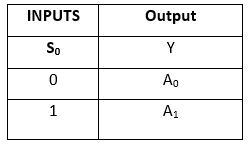
Igazságtáblázat:

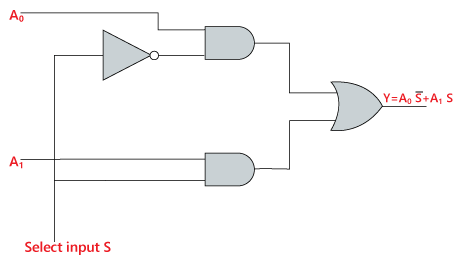
Az Y kifejezés logikai kifejezése a következő:

Y=S0′.A0+S0.A1

A fenti kifejezés logikai áramköre az alábbi:

4×1 multiplexer:

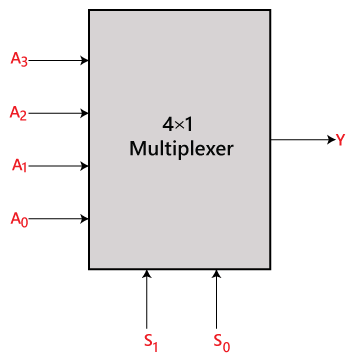
A 4×1 multiplexerben összesen négy bemenet van, azaz, A0, A1, A2 és A3, 2 választóvonal, azaz S0 és S1, és egyetlen kimenet, azaz Y. Az S0 és S1 választóvonalakon lévő bemenetek kombinációja alapján e 4 bemenet közül az egyik a kimenethez kapcsolódik. A 4×1 multiplexer blokkdiagramja és igazságtáblázata az alábbiakban látható.

blokkdiagram:

igazságtáblázat:

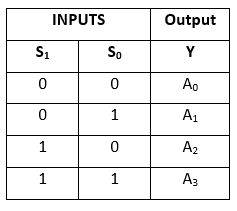
Az Y kifejezés logikai kifejezése a következő:

Y=S1′ S0′ A0+S1′ S0 A1+S1 S0′ A2+S1 S0 A3

A fenti kifejezés logikai áramköre az alábbi:

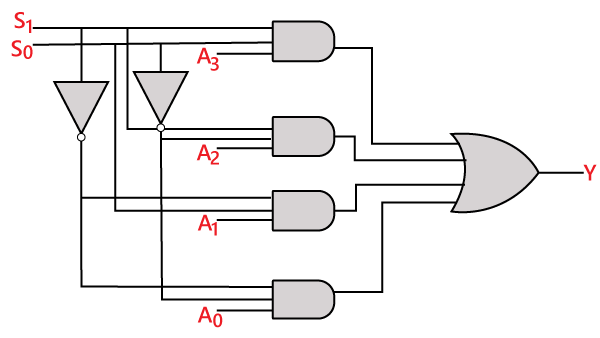
8-1 multiplexer

A 8-1 multiplexerben összesen nyolc bemenet van, i.e., A0, A1, A2, A3, A4, A5, A6 és A7, 3 választóvonal, azaz S0, S1és S2, és egyetlen kimenet, azaz Y. Az S0, S1 és S2 választóvonalakon lévő bemenetek kombinációja alapján e 8 bemenet közül az egyik a kimenethez kapcsolódik. A 8×1 multiplexer blokkdiagramja és igazságtáblázata az alábbiakban látható.

Blokkdiagram:

Igazságtáblázat:

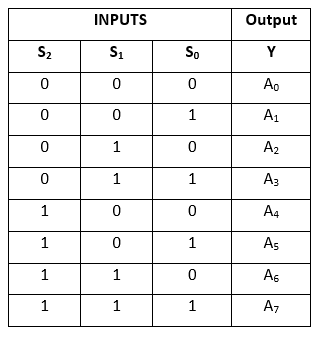
Az Y kifejezés logikai kifejezése a következő:

Y=S0′.S1′.S2′.A0+S0.S1′.S2′.A1+S0′.S1.S2′.A2+S0.S1.S2′.A3+S0′.S1′.S2 A4+S0.S1′.S2 A5+S0′.S1.S2 .A6+S0.S1.S3.A7

A fenti kifejezés logikai áramköre a következő:

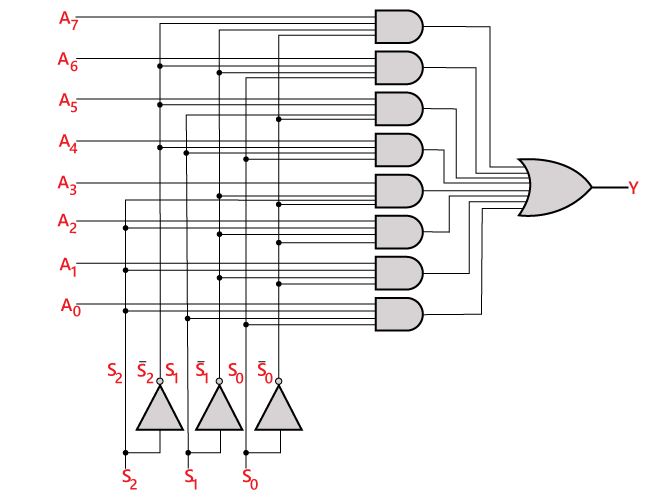
8×1 multiplexer 4×1 és 2×1 multiplexer felhasználásával

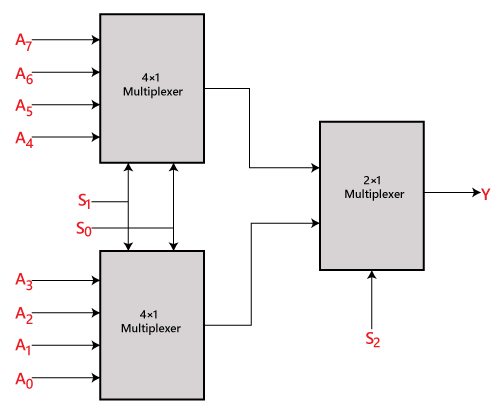
A 8×1 multiplexert alacsonyabb rendű multiplexerrel valósíthatjuk meg. A 8×1 multiplexer megvalósításához két 4×1 multiplexerre és egy 2×1 multiplexerre van szükségünk. A 4×1 multiplexer 2 választóvonallal, 4 bemenettel és 1 kimenettel rendelkezik. A 2×1 multiplexer csak 1 kiválasztó vonallal rendelkezik.

A 8 adatbemenet eléréséhez két 4×1 multiplexerre van szükségünk. A 4×1 multiplexer egy kimenetet állít elő. Tehát a végső kimenethez egy 2×1 multiplexerre van szükségünk. A 8×1 multiplexer blokkdiagramja 4×1 és 2×1 multiplexer használatával az alábbiakban látható.

16-1 multiplexer

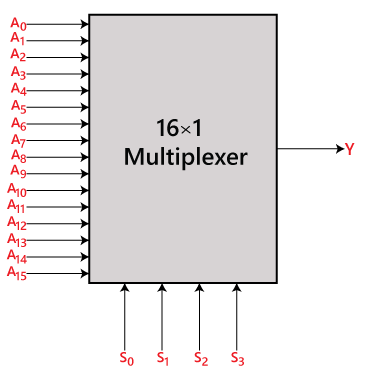
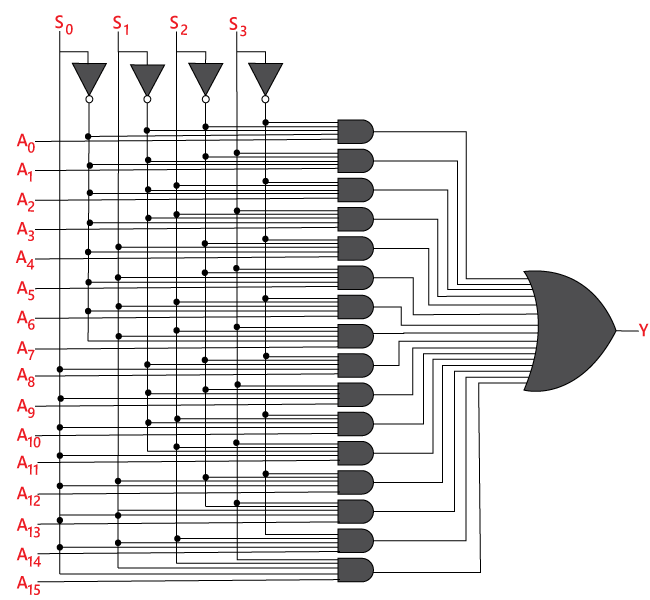
A 16-1 multiplexerben összesen 16 bemenet van, azaz A0, A1, …, A16, 4 választóvonal, azaz, S0, S1, S2 és S3, és egyetlen kimenet, azaz Y. Az S0, S1 és S2 választóvonalakon lévő bemenetek kombinációja alapján a 16 bemenet közül az egyik a kimenethez csatlakozik. A 16×1

blokkdiagram és igazságtáblázat:

igazságtáblázat:

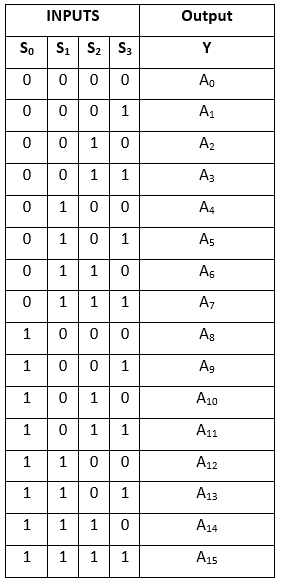
Az Y kifejezés logikai kifejezése a következő:

A fenti kifejezés logikai áramköre az alábbi:

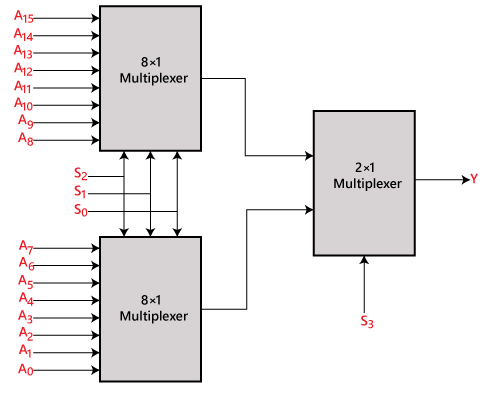
16×1 multiplexer 8×1 és 2×1 multiplexer felhasználásával

A 16×1 multiplexert egy alacsonyabb rendű multiplexer segítségével valósíthatjuk meg. A 8×1 multiplexer megvalósításához két 8×1 multiplexerre és egy 2×1 multiplexerre van szükségünk. A 8×1 multiplexer 3 választóvonallal, 4 bemenettel és 1 kimenettel rendelkezik. A 2×1 multiplexer csak 1 kiválasztó vonallal rendelkezik.

A 16 adatbemenet eléréséhez két 8×1 multiplexerre van szükségünk. A 8×1 multiplexer egy kimenetet állít elő. Tehát a végső kimenethez egy 2×1 multiplexerre van szükségünk. A 16×1 multiplexer blokkdiagramja a 8×1 és a 2×1 multiplexer használatával az alábbiakban látható.