Confronto tra PATRICIA Trie, con i suoi dadi e bulloni, e Hash Map

Nel microcosmo in cui sono inserito, la struttura dati trie non è così popolare. Questo ambiente è composto principalmente da scienziati di dati e, in un numero minore, da ingegneri del software, che lavorano con l’elaborazione del linguaggio naturale (NLP).

Recentemente mi sono trovato in un’interessante discussione su quando usare trie o hash table. Anche se non c’era nulla di nuovo in quella discussione che posso riportare qui, come i pro e i contro di ciascuna di queste due strutture dati (se cercate un po’ su Google troverete molti link che le trattano), ciò che era nuovo per me era un tipo speciale di trie chiamato Patricia Trie e, che in alcuni scenari, questa struttura dati ha prestazioni comparabili sia nel tempo di elaborazione che nello spazio con la tabella hash, mentre affronta compiti come elencare stringhe con prefisso comune senza costi aggiuntivi.

Con questo in mente, ho cercato una storia o un blog che mi aiutasse a capire in modo semplice (eufemismo per pigrizia) come funziona l’algoritmo PATRICIA, specialmente come scorciatoia per leggere il documento di 21 pagine pubblicato nel 1968. Sfortunatamente non sono riuscito in questa ricerca, lasciandomi senza alternative alla lettura.

Il mio obiettivo con questa storia è quello di colmare la suddetta lacuna, cioè, avere una storia che descriva in termini profani l’algoritmo in questione.

Per raggiungere il mio obiettivo, prima, e brevemente, introdurrò, per chi non ha familiarità con i tentativi, questa struttura dati. Dopo questa introduzione, elencherò i trie più popolari là fuori, permettendomi di implementare e descrivere in dettaglio come funziona PATRICIA Trie e perché si comportano così bene. Concluderò questa storia confrontando i risultati (prestazioni e consumo di spazio) in due diverse applicazioni: la prima è un conteggio di parole (<WORD, FREQUENCY> tuple) basato su un testo abbastanza grande; e la seconda è la costruzione di un <URL, IP> tuple, basato su una lista di più di 2 milioni di URL, che consiste nell’elemento centrale di un server DNS. Entrambe le applicazioni sono state costruite sulla base di Hash Map e Patricia Trie.

Come definito da Sedgewick e Wayne della Princeton University nel loro libro Algorithms – Fourth Edition (editore: Addison-Wesley) un trie, o albero dei prefissi, è “una struttura dati costruita dai caratteri della chiave di ricerca per guidare la ricerca”. Questa “struttura di dati è composta da nodi che contengono collegamenti che sono nulli o riferimenti ad altri nodi. Ogni nodo è indicato da un solo altro nodo, che è chiamato il suo genitore (ad eccezione di un nodo, la radice, che non ha nodi che puntano ad esso), e ogni nodo ha S collegamenti, dove S è la dimensione dell’alfabeto (o charset)”.

La figura 1 qui sotto, seguendo la definizione di cui sopra, contiene un esempio di un trie.

Il nodo radice non ha etichetta. Ha tre figli: nodi con chiave ‘a’, ‘h’ e ‘s’. Nell’angolo in basso a destra della figura c’è una tabella che elenca tutte le chiavi con il loro rispettivo valore. Dalla radice possiamo passare ad ‘a’ -> ‘i’ -> ‘r’. Questa sequenza forma la parola “air” con valore (per esempio il numero di volte che questa parola appare in un testo) di 4 (i valori sono dentro un riquadro verde). Per convenzione, una parola esistente in una tabella di simboli ha un valore non nullo. Così, mentre la parola “airway” esiste in inglese, non è in questo trie, perché, seguendo la convenzione, il valore del nodo con chiave ‘y’ è nullo.

La parola “air” è anche il prefisso delle parole: “aereo”; e “vie aeree”. La sequenza ‘h’ -> ‘a’ forma il prefisso di “ha” e “cappello” come la sequenza ‘h’ -> ‘o’ forma il prefisso di “casa” e “cavallo”.

Oltre a servire bene come struttura dati per, diciamo, un dizionario, serve anche come elemento importante di un’applicazione di completamento. Un sistema potrebbe proporre le parole “aereo” e “vie aeree” dopo che un utente ha digitato la parola “aria”, attraversando il sottoalbero la cui radice è il nodo con chiave “r”. Un ulteriore vantaggio di questa struttura è che si può ottenere una lista ordinata delle chiavi esistenti, senza alcun costo aggiuntivo, attraversando il trie in modo ordinato, impilando i figli di un nodo e attraversandoli da sinistra a destra.

Nella figura 2 è esemplificata l’anatomia del nodo.

La parte interessante in questa anatomia è che i puntatori ai figli sono solitamente memorizzati in un array. Se stiamo rappresentando un set di caratteri S, per esempio, ASCII esteso, abbiamo bisogno che l’array sia di dimensione 256. Avendo un carattere figlio possiamo accedere al suo puntatore nel suo genitore in tempo O(1). Considerando che la dimensione del vocabolario è N e che la dimensione della parola più lunga è M, la profondità del trie è anche M e ci vuole O(MN) per attraversare la struttura. Se consideriamo che normalmente N è molto più grande di M (il numero di parole in un corpus è molto più grande della dimensione della parola più lunga), possiamo considerare O(MN) come lineare. In pratica questo array è rado, cioè la maggior parte dei nodi ha molti meno figli di S. Inoltre la dimensione media delle parole è anche più piccola di M, quindi, in pratica, in media, ci vuole O(logₛ N) per cercare una chiave e O(N logₛ N) per attraversare l’intera struttura.

Ci sono due problemi principali con questa struttura dati. Uno è il consumo di spazio. Ad ogni livello L, a partire da zero, ci sono, assimptoticamente, Sᴸ puntatori. Se con l’ASCII esteso, cioè 256 caratteri, questo è un problema in dispositivi di memoria limitata, la situazione peggiora se si considerano tutti i caratteri Unicode (65.000). Il secondo è la quantità di nodi con un solo figlio, degradando le prestazioni di input e di ricerca. Nell’esempio della figura 1 solo la radice, la chiave ‘h’ al livello 1, le chiavi ‘a’ e ‘o’ al livello 2 e la chiave ‘r’ al livello 3 hanno più di un figlio. In altre parole, solo 5 nodi su 27 hanno due o più figli. Le alternative a questa struttura affrontano principalmente questi problemi.

Prima di descrivere l’alternativa (PATRICIA Trie), risponderò alla seguente domanda: perché le alternative se possiamo usare una tabella hash invece di un array? La tabella hash aiuta davvero a risparmiare memoria con poco degrado delle prestazioni, ma non risolve il problema. Più in alto si è nel trie (più vicino al livello zero) è più probabile che quasi tutti i caratteri di qualsiasi charset debbano essere indirizzati. Le tabelle hash ben implementate, come quella in Java (sicuramente tra le migliori, probabilmente la migliore), iniziano con una dimensione predefinita e si ridimensionano automaticamente secondo una soglia. In Java la dimensione predefinita è 16 con una soglia di 0,75 e raddoppia la sua dimensione in ciascuna di queste operazioni. Considerando l’ASCII esteso, quando il numero di bambini in un nodo raggiunge 192, la tabella hash sarà ridimensionata a 512, anche se alla fine ne servono solo 256.

Radix Trie

Poiché PATRICIA Trie è un caso speciale di Radix Trie, inizierò con quest’ultimo. In Wikipedia un Radix Trie è definito come “una struttura di dati che rappresenta un trie ottimizzato nello spazio… in cui ogni nodo che è l’unico figlio è fuso con il suo genitore… A differenza degli alberi regolari (dove intere chiavi sono confrontate in massa dal loro inizio fino al punto di disuguaglianza), la chiave di ogni nodo è confrontata pezzo di bit per pezzo di bit, dove la quantità di bit in quel pezzo in quel nodo è il radix r del radix trie”. Questa definizione avrà più senso quando esemplificheremo questo trio nella figura 3.

Il numero di figli r di un nodo in una trie radix è determinato dalla seguente formula dove x è il numero di bit richiesto per confrontare il chunk-of-bits di cui sopra:

La formula sopra stabilisce che il numero di figli in una Trie Radix sia sempre un multiplo di 2. Per esempio, per una 4-Radix Trie, x = 2. Questo significa che dovremmo confrontare pezzi di due bit, una coppia di bit, perché con questi due bit rappresentiamo tutti i numeri decimali da 0 a 3, per un totale di 4 numeri diversi, uno per ogni figlio.

Per capire meglio le definizioni precedenti, consideriamo l’esempio in figura 3. In questo esempio abbiamo un ipotetico set di caratteri composto da 5 caratteri (NULL, A, B, C e D). Ho scelto di rappresentarli usando solo 4 bit (tenete presente che questo non ha niente a che fare con r, si ha bisogno solo di 3 bit per rappresentare 5 caratteri, ma ha a che fare con la facilità di disegnare l’esempio). Nell’angolo in alto a sinistra della figura c’è una tabella che mappa ogni carattere alla sua rappresentazione in bit.

Per inserire il carattere ‘A’, lo confronterò bit per bit con quello NULL. Nell’angolo in alto a destra della figura 3, all’interno della casella etichettata con 1 in un diamante giallo, possiamo vedere che questi due caratteri differiscono alla prima coppia. Questa prima coppia è rappresentata in rosso nella rappresentazione a 4 bit di A. Quindi DIFF contiene la posizione del bit dove finisce la coppia diversa.

Per inserire il carattere ‘B’ dobbiamo confrontarlo bitwise con il carattere ‘A’. Questo confronto è nella casella di diamante etichettata con 2. La differenza cade questa volta sulla seconda coppia di bit, in rosso, che termina alla posizione 4. Poiché la seconda coppia è 01, creiamo il nodo con la chiave B e puntiamo l’indirizzo 01 del nodo A ad esso. Questo collegamento può essere visto nella parte inferiore della figura 3. La stessa procedura si applica per inserire i caratteri ‘C’ e ‘D’.

Nell’esempio precedente vediamo che la prima coppia (01 in blu) è il prefisso di tutti i caratteri inseriti.

Questo esempio serve a descrivere il confronto chunk-of-bits, l’ottimizzazione dello spazio (solo quattro figli in questo caso, indipendentemente dalla dimensione del set di caratteri) e la fusione genitore/figlio (memorizzati nei nodi figli solo i bit che differiscono dalla radice) menzionati nella definizione Radix Trie sopra. Tuttavia, c’è ancora un collegamento che punta a un nodo nullo. La scarsità è direttamente proporzionale a r e alla profondità del trie.

PATRICIA Trie

PATRICIA (Practical Algorithm to Retrieve Information Coded in Alphanumeric, Journal of the ACM, 15(4):514-534, October 1968) . Sì, PATRICIA è un acronimo!

PATRICIA Trie è qui definita da tre regole:

1. Ogni nodo (TWIN è il termine originale di PATRICIA) ha due figli (r = 2 e x = 1 nei termini Radix Trie);
2. Un nodo si divide in un prefisso (L-PHRASE nei termini di PATRICIA) con due figli (ogni figlio forma un BRANCH che è il termine originale di PATRICIA) solo se due parole (PROPER OCCURRENCE nei termini di PATRICIA) hanno lo stesso prefisso; e
3. Ogni parola che termina sarà rappresentata con un valore all’interno del nodo diverso da null (segno di FINE nella nomenclatura originale di PATRICIA)

La regola numero 2 sopra implica che la lunghezza del prefisso ad ogni livello sia maggiore della lunghezza del prefisso del livello precedente. Questo sarà molto importante negli algoritmi che supportano le operazioni PATRICIA come inserire un elemento o trovarne un altro.

Dalle regole precedenti si può definire il nodo come illustrato qui sotto. Ogni nodo ha un genitore, eccetto la radice, e due figli, un valore (qualsiasi tipo) e una variabile diff che indica la posizione in cui si trova la divisione nella chiave bitcode

Per utilizzare l’algoritmo PATRICIA abbiamo bisogno di una funzione che, date 2 stringhe, restituisca la posizione del primo bit, da sinistra a destra, dove differiscono. Abbiamo già visto che questo funziona per Radix Trie.

Per operare il trie usando PATRICIA, cioè per inserire o trovare chiavi in esso, abbiamo bisogno di 2 puntatori. Uno è parent, inizializzato puntando al nodo radice. Il secondo è child, inizializzato facendolo puntare al figlio sinistro di root.

Su ciò che segue la variabile diff conterrà la posizione in cui la chiave da inserire differisce da child.key. Seguendo la regola numero 2 definiamo le seguenti 2 disequazioni:

Lascia che found punti al nodo dove la ricerca di una chiave finisce. Se found.key è diverso dalla stringa da inserire, il diff sarà calcolato, tramite una funzione ComputeDiff, usando questa stringa e found.key. Se sono uguali, la chiave esiste nella struttura e, come in qualsiasi tabella di simboli, il valore dovrebbe essere restituito. Un metodo helper chiamato BitAtPosition, che recupera il bit in una posizione specifica (0 o 1), sarà usato durante le operazioni.

Per cercare dobbiamo definire una funzione Search(key). Il suo pseudocodice è in figura 4.

La seconda funzione che useremo in questa storia è la Insert(key). Il suo pseudocodice è in figura 6.

Nello pseudocodice di cui sopra c’è un metodo per creare un nodo chiamato CreateNode. I suoi argomenti possono essere compresi dalla figura 4.

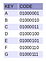
Per esemplificare come funziona un PATRICIA Trie, preferisco guidare il lettore in un’operazione passo dopo passo per completare l’inserimento di 7 caratteri (‘A’, ‘B’, ‘C’, ‘D’, ‘E’, ‘F’ e ‘G’ come specificato nella figura 7 qui accanto) nel loro ordine naturale. Alla fine, si spera, si sarà capito come funziona questa struttura di dati.

Il carattere A è il primo ad essere inserito. Il suo bitcode è 01000001. Come con Radix Trie, confronteremo questo bitcode con quello alla radice che in questo momento è nullo, quindi confrontiamo 00000000 con 01000001. La differenza cade nella posizione 2 (qui come x = 1 stiamo confrontando bit per bit invece di una coppia di essi).

Per creare il nodo dobbiamo puntare il figlio sinistro e destro ai loro rispettivi successori. Poiché questo nodo è la radice, per definizione, il suo figlio sinistro punta a se stesso mentre il figlio destro punta a null. Questo sarà l’unico puntatore nullo in tutto il trio. Ricordando che la radice è l’unico nodo senza genitori. Il valore, nel nostro esempio sarà un numero intero che imita un’applicazione di conteggio di parole, è impostato a 1. Il risultato di questa operazione di inserimento è mostrato nella figura 8.

Prossimo inseriamo il carattere B con il codice bit 01000010. La prima cosa da fare è controllare se questo carattere è già presente nella struttura. Per fare questo lo cercheremo. La ricerca in un Trie di PATRICIA è semplice (vedi pseudocodice in figura 5). Dopo aver confrontato la chiave di root con B si conclude che sono diverse, quindi si procede creando 2 puntatori: parent e child. Inizialmente parent punta alla radice e child punta al figlio sinistro della radice. In questo caso entrambi puntano al nodo A. Seguendo la regola numero 2, itereremo la struttura mentre la disequazione (1) è vera.

In questo momento parent.DIFF è uguale e non inferiore a child.DIFF. Questo rompe la disequazione (1). Poiché il child.VALUE è diverso da null (uguale a 1) confrontiamo i caratteri. Poiché A è diverso da B, questo significa che B non è nel trie e deve essere inserito.

Per inserire iniziamo, di nuovo, definendo genitore e figlio come prima, cioè, genitore punta alla radice e figlio punta al suo nodo sinistro. L’iterazione attraverso la struttura deve seguire le disequazioni (1) e (2). Continuiamo calcolando diff, che è la differenza, in senso bit, tra B e child.KEY, che a questo punto è uguale ad A (differenza tra i bitcode 01000001 e 01000010) . La differenza cade sul bit in posizione 7, quindi diff = 7.

In questo momento parent e child puntano allo stesso nodo (al nodo A, la radice). Poiché la disequazione (1) è già falsa e child.DIFF è minore di diff, creeremo il nodo B e punteremo parent.LEFT ad esso. Come abbiamo fatto con il nodo A, dobbiamo puntare i figli del nodo B da qualche parte. Il bit in posizione 7 in B è 1, quindi il figlio B destro del nodo punterà a se stesso. Il figlio B sinistro del nodo punterà al genitore, la radice in questo caso. Il risultato finale è mostrato nella figura 9.

Indirizzando il figlio B sinistro del nodo al suo genitore stiamo abilitando la divisione menzionata nella regola numero 2. Quando inseriamo un carattere il cui diff cade tra 2 e 7 questo puntatore ci rimanda alla posizione corretta da cui si inserisce il nuovo carattere. Questo accadrà quando inseriamo il carattere D.

Ma prima dobbiamo inserire il carattere C con bitcode uguale a 01000011. Il puntatore parent punterà al nodo A (la radice). Questa volta, diversamente da quando stavamo cercando il carattere B, il bambino punta al nodo B (in quel momento entrambi i puntatori puntavano alla radice).

In questo momento la disuguaglianza (1) è valida (parent.DIFF è inferiore a child.DIFF) quindi aggiorniamo entrambi i puntatori, impostando parent a child e child a child B right del nodo perché alla posizione 7 il bit di C è 1.

Dopo l’aggiornamento entrambi i puntatori puntano al nodo B, spezzando la disuguaglianza (1). Come abbiamo fatto prima, confrontiamo il bitcode di child.KEY con il bitcode di C (01000010 con 01000011) concludendo che differiscono nella posizione 8. Poiché alla posizione 7 il bit di C è 1, questo nuovo nodo (nodo C) sarà il figlio destro di B. Alla posizione 8 il bit di C è 1, facendoci impostare il figlio destro del nodo C su se stesso, mentre il suo figlio sinistro punta al genitore, il nodo B in questo momento. Il trio risultante è in figura 10.

Il prossimo carattere è D (codice bit 01000100). Come abbiamo fatto con l’inserimento del carattere C, impostiamo inizialmente il puntatore parent al nodo A e il puntatore child al nodo B. La disequazione (1) è valida quindi aggiorniamo i puntatori. Ora il genitore punta al nodo B e il figlio punta al figlio sinistro del nodo B, perché nella posizione 7 il bit di D è 0. A differenza dell’inserimento del carattere C, ora il figlio punta di nuovo al nodo A, rompendo la disequazione (1). Ancora una volta calcoliamo la differenza tra i bitcode A e D. Ora la diff è 6. Ora la diff è 6. Di nuovo impostiamo genitore e figlio come facciamo normalmente. Ora, mentre la disequazione (1) è valida, la disequazione (2) non lo è. Questo implica che inseriremo D come figlio sinistro di A. Ma che dire dei figli di D? Alla posizione 6 il bit di D è 1 quindi il suo figlio destro punta a se stesso. La parte interessante è che il figlio sinistro del nodo D ora punterà al nodo B raggiungendo il trio disegnato in figura 11.

Il prossimo è il carattere E con bitcode 01000101. La funzione di ricerca restituisce il nodo D. La differenza tra i caratteri D ed E cade sul bit in posizione 8. Poiché alla posizione 6 il bit di E è 1, sarà posizionato alla destra di D. La struttura del trie è illustrata nella figura 12.

La cosa interessante inserendo il carattere F è che il suo posto è tra i caratteri D ed E, perché la differenza tra D ed F è in posizione 7. Ma alla posizione 7 il bit di E è 0, quindi il nodo E sarà il figlio sinistro del nodo F. La struttura è ora illustrata nella figura 13.

E, infine, inseriamo il carattere G. Dopo tutti i calcoli concludiamo che il nuovo nodo dovrebbe essere posto come figlio destro del nodo F con diff uguale a 8. Il risultato finale è in figura 14.

Finora stiamo inserendo stringhe composte da un solo carattere. Cosa succederebbe se provassimo a inserire le stringhe AB e BA? Il lettore interessato può prendere questa proposizione come esercizio. Due suggerimenti: entrambe le stringhe differiscono dal nodo B nella posizione 9; e il trie finale è illustrato nella figura 15.

Pensando all’ultima figura, si può porre la seguente domanda: Per trovare, ad esempio, la stringa BA sono necessari 5 confronti di bit, mentre per calcolare il codice hash di questa stringa sono necessarie solo due iterazioni, quindi quando PATRICIA Trie diventa competitivo? Immaginate se inseriamo in questa struttura la stringa ABBABABBBBABABBA (presa dall’esempio del documento originale PATRICIA del 1968) che è lunga 16 caratteri? Questa stringa sarebbe posta come figlio sinistro del nodo AB con diff alla posizione 17. Per trovarla, avremmo bisogno di 5 confronti di bit, mentre per calcolare il codice hash ci vorrebbero 16 iterazioni, una per ogni carattere, questa è la ragione per cui PATRICIA Trie è così competitivo nella ricerca di lunghe stringhe.

PATRICIA Trie vs Hash Map

In questa ultima sezione confronterò Hash Map e PATRICIA Trie in due applicazioni. La prima è un conteggio di parole su leipzig1m.txt contenente 1 milione di frasi casuali e la seconda è il popolamento di una tabella di simboli con più di 2,3 milioni di URL dal progetto DMOZ (chiuso nel 2017) scaricato da qui.

Il codice che ho sviluppato e utilizzato sia per implementare lo pseudocodice sopra che per confrontare le prestazioni di PATRICIA Trie con Hash Table può essere trovato sul mio GitHub.

Questi confronti sono stati effettuati nella mia macchina Ubuntu 18.04. La configurazione può essere trovata nella figura 16

.