I de mikrokosmos, jeg er indlejret i, er trie-datastrukturer som dem, der ligner dem, ikke så populære. Dette miljø består hovedsageligt af dataloger og i et mindre antal softwareingeniører, der arbejder med Natural Language Processing (NLP).
For nylig befandt jeg mig i en interessant diskussion om, hvornår man skal bruge trie eller hash table. Selv om der ikke var noget nyt i den diskussion, som jeg kan rapportere her, som fordele og ulemper ved hver af disse to datastrukturer (hvis du googler lidt, finder du mange links, der behandler dem), var det nye for mig en særlig type trie kaldet Patricia Trie, og, at i nogle scenarier, denne datastruktur udfører sammenligneligt både i behandlingstid og plads med hash tabel, samtidig med at den behandler opgaver som at liste strenge med fælles præfiks uden ekstra omkostninger.
Med dette i tankerne søgte jeg efter en historie eller en blog, der kunne hjælpe mig med at forstå på en enkel måde (eufemisme for dovenskab), hvordan PATRICIA-algoritmen fungerer, og som specielt tjente som en genvej til at læse det 21 sider lange papir, der blev offentliggjort i 1968. Desværre lykkedes det mig ikke med denne søgning, hvilket efterlod mig uden alternativ til at læse det.
Min målsætning med denne historie er at udfylde ovenstående hul, dvs. at have en historie, der i lægmandstermer beskriver den foreliggende algoritme.
For at nå mit mål vil jeg først og kort introducere, for dem der ikke er bekendt med forsøg, denne datastruktur. Efter denne introduktion vil jeg liste de mest populære trie derude, hvilket gør det muligt for mig at implementere og beskrive i detaljer, hvordan PATRICIA Trie fungerer, og hvorfor de klarer sig så godt. Jeg vil afslutte denne historie med at sammenligne resultaterne (ydeevne og pladsforbrug) i to forskellige applikationer: den første er en ordtælling (<WORD, FREQUENCY> tupler) baseret på en ret stor tekst; og den anden er opbygning af en <URL, IP> tupler, baseret på en liste med mere end 2 millioner URL’er, der består i kerneelementet i en DNS-server. Begge programmer blev bygget på grundlag af Hash Map og Patricia Trie.
Som defineret af Sedgewick og Wayne fra Princeton University i deres bog Algorithms – Fourth Edition (forlag: Addison-Wesley) er en trie, eller præfikseringstræ, “en datastruktur, der er opbygget ud fra søgenøglens tegn for at styre søgningen”. Denne “datastruktur er sammensat af knuder, der indeholder links, som enten er nul eller refererer til andre knuder. Hver knude peger kun på én anden knude, som kaldes dens forælder (bortset fra én knude, roden, som ikke har nogen knuder, der peger på den), og hver knude har S links, hvor S er alfabetets størrelse (eller charset)”.
Figur 1 nedenfor indeholder, efter ovenstående definition, et eksempel på en trie.

Rodknuden har ingen label. Den har tre børn: knuder med nøglen “a”, “h” og “s”. I det nederste højre hjørne af figuren er der en tabel med en liste over alle nøgler med deres respektive værdi. Fra roden kan vi bevæge os til ‘a’ -> ‘i’ -> ‘r’. Denne sekvens danner ordet “air” med en værdi (f.eks. det antal gange dette ord forekommer i en tekst) på 4 (værdierne er inden for en grøn boks). Som konvention har et eksisterende ord i en symboltabel en værdi, der ikke er nul. Så selv om ordet “airway” findes på engelsk, findes det ikke i denne trie, fordi værdien af noden med nøglen “y” ifølge konventionen er nul.
Ordet “air” er også præfikset for ordene: “airplane”; og “airways”. Sekvensen ‘h’ -> ‘a’ danner præfikset til “har” og “hat”, ligesom sekvensen ‘h’ -> ‘o’ danner præfikset til “hus” og “hest”.
Udover at fungere godt som datastruktur for, lad os sige, en ordbog, tjener den også som et vigtigt element i et kompletteringsprogram. Et system kunne foreslå ordene “airplane” og “airways”, efter at en bruger har indtastet ordet “air”, ved at gennemløbe undertræet, hvis rod er knuden med nøglen “r”. En yderligere fordel ved denne struktur er, at man uden yderligere omkostninger kan få en ordnet liste over de eksisterende nøgler ved at gennemløbe trien i rækkefølge, idet man stabler en knudes børn og gennemløber dem fra venstre mod højre.
I figur 2 er nodens anatomi eksemplificeret.

Den interessante bit i denne anatomi er, at pointere til børn normalt gemmes i et array. Hvis vi repræsenterer et tegnsæt S af f.eks. udvidet ASCII, skal arrayet have en størrelse på 256. Når vi har et barns tegn, kan vi få adgang til dets pointer i dets forælder på O(1)-tid. I betragtning af at ordforrådets størrelse er N, og at størrelsen af det længste ord er M, er trie’ens dybde også M, og det tager O(MN) at gennemløbe strukturen. Hvis vi tager i betragtning, at N normalt er meget større end M (antallet af ord i et korpus er meget større end størrelsen af det længste ord), kan vi anse O(MN) for at være lineær. I praksis er dette array sparsomt, dvs. at størstedelen af knuderne har langt færre børn end S. Desuden er den gennemsnitlige størrelse af ordene også mindre end M, således at det i praksis i gennemsnit tager O(logₛ N) at søge efter en nøgle og O(N logₛ N) at gennemløbe hele strukturen.
Der er to hovedproblemer med denne datastruktur. Det ene er pladsforbruget. På hvert niveau L, begyndende med nul, er der, assimptotisk set, Sᴸ pointere. Hvis dette med Extended ASCII, dvs. 256 tegn, er et problem i begrænsede hukommelsesenheder, forværres situationen, hvis man tager alle Unicode-tegn (65.000 af dem) i betragtning. Det andet problem er antallet af knuder med kun ét barn, hvilket forringer indtastnings- og søgeydelsen. I eksemplet i figur 1 er det kun roden, nøglen “h” på niveau 1, nøglerne “a” og “o” på niveau 2 og nøglen “r” på niveau 3, der har mere end ét barn. Med andre ord har kun 5 knuder ud af de 27 knuder to eller flere børn. Alternativerne til denne struktur tager primært fat på disse problemer.
Hvor jeg beskriver alternativet (PATRICIA Trie), vil jeg besvare følgende spørgsmål: Hvorfor alternativer, hvis vi kan bruge en hashtabel i stedet for et array? Hashtabellen er virkelig med til at spare hukommelse med lille ydelsesforringelse, men løser ikke problemet. Jo højere man befinder sig i trien (tættere på niveau nul), jo mere sandsynligt er det, at næsten alle tegn i et hvilket som helst charset skal adresseres. Godt implementerede hashtabeller, som f.eks. den i Java (absolut blandt de bedste, måske endda den bedste), starter med en standardstørrelse og ændrer automatisk størrelsen i henhold til en tærskelværdi. I Java er standardstørrelsen 16 med en tærskelværdi på 0,75, og den fordobler sin størrelse i hver af disse operationer. Hvis man tager Extended ASCII i betragtning, vil hashtabellen, når antallet af børn i en knude når op på 192, have en størrelse på 512, selv om den kun har brug for 256 til sidst.
Radix Trie
Da PATRICIA Trie er et specialtilfælde af Radix Trie, vil jeg starte med sidstnævnte. I Wikipedia defineres en Radix Trie som “en datastruktur, der repræsenterer en pladsoptimeret trie … hvor hver knude, der er det eneste barn, er slået sammen med sin forælder … I modsætning til almindelige træer (hvor hele nøgler sammenlignes en masse fra deres begyndelse og frem til punktet for ulighed), sammenlignes nøglen ved hver knude chunk-of-bits for chunk-of-bits, hvor mængden af bits i den chunk ved den pågældende knude er radix r i radix trie”. Denne definition vil give mere mening, når vi illustrerer denne trie i figur 3.
Antallet af børn r for et knudepunkt i en radix-trie bestemmes ved følgende formel, hvor x er det antal bits, der kræves for at sammenligne ovennævnte chunk-of-bits:
Overstående formel sætter antallet af børn i en radix-trie til altid at være et multiplum af 2. For en 4-Radix Trie er f.eks. x = 2. Det betyder, at vi ville være nødt til at sammenligne stykker på to bits, et par bits, fordi vi med disse to bits repræsenterer alle decimaltal fra 0 til 3, i alt 4 forskellige tal, et for hvert barn.
For bedre at forstå ovenstående definitioner kan vi se på eksemplet i figur 3. I dette eksempel har vi et hypotetisk tegnsæt, der består af 5 tegn (NULL, A, B, C og D). Jeg har valgt at repræsentere dem ved hjælp af kun 4 bits (husk, at dette ikke har noget at gøre med r, man behøver kun 3 bits for at repræsentere 5 tegn, men har at gøre med, at det er let at tegne eksemplet). I øverste venstre hjørne af figuren er der en tabel, der viser hver enkelt tegn til deres bitrepræsentation.
For at indsætte tegnet “A” vil jeg sammenligne det bitvis med NULL-tegnet. I det øverste højre hjørne af figur 3, i det felt, der er mærket med 1 i en gul diamant, kan vi se, at disse to tegn adskiller sig ved det første par. Dette første par er repræsenteret med rødt i A’s 4-bits repræsentation. DIFF indeholder altså den bitposition, hvor det forskellige par slutter.
For at indsætte tegn “B” skal vi sammenligne det bitvis med tegn “A”. Denne sammenligning er i diamantboksen mærket med 2. Forskellen falder denne gang på det andet bitpar, i rødt, som slutter på position 4. Da det andet par er 01, opretter vi en knude med nøglen B og peger adressen 01 på knude A til den. Denne forbindelse kan ses i den nederste del af figur 3. Samme procedure gælder for indsættelse af tegn “C” og “D”.

I ovenstående eksempel ser vi, at det første par (01 i blåt) er præfikset for alle de indsatte tegn.
Dette eksempel tjener til at beskrive chunk-of-bits-sammenligning, pladsoptimering (kun fire børn i dette tilfælde, uanset tegnsættets størrelse) og forældre/barn-sammenlægning (kun de bits, der adskiller sig fra roden, lagres i børnenes knudepunkter), der er nævnt i Radix Trie-definitionen ovenfor. Ikke desto mindre er der stadig et link, der peger på et nulknudepunkt. Sparsomheden er direkte proportional med r og trie’s dybde.
PATRICIA Trie
PATRICIA (Practical Algorithm to Retrieve Information Coded in Alphanumeric, Journal of the ACM, 15(4):514-534, October 1968) . Ja, PATRICIA er et akronym!
PATRICIA Trie er her defineret ved hjælp af tre regler:
- Hver knude (TWIN er PATRICIAs oprindelige term) har to børn (r = 2 og x = 1 i Radix Trie-termer);
- En knude opdeles kun i et præfiks (L-PHRASE i PATRICIAs termer) med to børn (hvert barn danner en BRANCH, som er PATRICIAs oprindelige term), hvis to ord (PROPER OCCURRENCE i PATRICIAs termer) har det samme præfiks; og
- Hvert ord, der slutter, vil blive repræsenteret med en værdi i knuden, der er forskellig fra nul (END-tegn i PATRICIAs oprindelige nomenklatur)
Regel nummer 2 ovenfor indebærer, at præfiksets længde på hvert niveau er større end præfiksets længde fra det foregående niveau. Dette vil være meget vigtigt i de algoritmer, der understøtter PATRICIA-operationer som f.eks. at indsætte et element eller finde et andet.
Med udgangspunkt i ovenstående regler kan man definere knuden som illustreret nedenfor. Hver node har én forælder, bortset fra roden, og to børn, en værdi (enhver type) og en variabel diff, der angiver den position, hvor splittet er i nøglebitkoden

For at bruge PATRICIA-algoritmen har vi brug for en funktion, der, givet to strenge, returnerer positionen af den første bit, fra venstre mod højre, hvor de er forskellige. Vi har allerede set, at dette fungerer for Radix Trie.
For at betjene trien ved hjælp af PATRICIA, dvs. for at indsætte eller finde nøgler i den, har vi brug for 2 pointere. Den ene er parent, initialiseret ved at pege den til rodknuden. Den anden er child, initialiseret ved at pege den til rodens venstre barn.
I det følgende vil variablen diff indeholde den position, hvor den nøgle, der indsættes, adskiller sig fra child.key. Efter regel nummer 2 definerer vi følgende 2 uligninger:
Let fundet peger på den knude, hvor søgningen efter en nøgle slutter. Hvis found.key er forskellig fra den streng, der indsættes, vil diff blive beregnet via en ComputeDiff-funktion ved hjælp af denne streng og found.key. Hvis de er ens, findes nøglen i strukturen, og som i enhver symboltabel skal værdien returneres. En hjælpemetode kaldet BitAtPosition, der henter bitten på en bestemt position (0 eller 1), vil blive brugt under operationerne.
For at søge skal vi definere en Search(key)-funktion. Dens pseudokode er i figur 4.

Den anden funktion, vi skal bruge i denne historie, er Insert(key). Dens pseudokode er i figur 6.

I ovenstående pseudokode er der en metode til at oprette en node kaldet CreateNode. Dens argumenter kan forstås af figur 4.
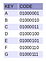
For at eksemplificere, hvordan en PATRICIA Trie fungerer, foretrækker jeg at guide læseren i en trinvis operation for at fuldføre indsættelsen af 7 tegn (“A”, “B”, “C”, “D”, “E”, “F” og “G” som angivet i figur 7 ved siden af) i deres naturlige rækkefølge. Til sidst har man forhåbentlig forstået, hvordan denne datastruktur fungerer.
Tegn A er det første, der skal indsættes. Dens bitkode er 01000001. Som med Radix Trie vil vi sammenligne denne bitkode med den i roden, som i dette øjeblik er nul, så vi sammenligner 00000000 med 01000001. Forskellen falder på position 2 (her da x = 1 sammenligner vi bit for bit i stedet for et par af dem).

For at oprette knuden skal vi pege det venstre og det højre barn til deres respektive efterfølgere. Da denne node er roden, peger dens venstre barn pr. definition på sig selv, mens dens højre barn peger på null. Dette vil være den eneste null-pointer i hele trien. Husk på, at roden er den eneste node uden nogen forælder. Værdien, som i vores eksempel vil være et heltal, der efterligner et program til at tælle ord, sættes til 1. Resultatet af denne indsætningsoperation er vist i figur 8.
Næst vil vi indsætte tegn B med bitkode 01000010. Det første er at kontrollere, om dette tegn allerede findes i strukturen. For at gøre dette vil vi søge efter det. Det er nemt at søge i en PATRICIA-trie (se pseudokode i figur 5). Efter at have sammenlignet rodens nøgle med B konkluderer man, at de er forskellige, så vi fortsætter ved at oprette to pointere: parent og child. I første omgang peger parent på roden, og child peger på rodens venstre barn. I dette tilfælde peger begge på knude A. I henhold til regel nr. 2 vil vi iterere strukturen, mens uligningen (1) er sand.
I dette øjeblik er parent.DIFF lig med, og ikke mindre end child.DIFF. Dette bryder uligningen (1). Da child.VALUE er forskellig fra null (lig med 1), sammenligner vi tegnene. Da A er forskellig fra B, betyder det, at B ikke er i trien og skal indsættes.
For at indsætte starter vi igen med at definere parent og child som før, dvs. at parent peger på roden og child peger på dens venstre knude. Iterationen gennem strukturen skal følge uligningerne (1) og (2). Vi fortsætter med at beregne diff, som er forskellen, bitvis, mellem B og child.KEY, som på dette tidspunkt er lig med A (forskellen mellem bitkoderne 01000001 og 01000010) . Forskellen falder på bit på position 7 , så diff = 7.

I dette øjeblik peger parent og child på den samme knude (på knude A, roden). Da uligning (1) allerede er falsk, og child.DIFF er mindre end diff, opretter vi knude B og peger parent.LEFT på den. Som vi gjorde med node A, skal vi pege node B’s børn til et eller andet sted hen. Bitten på position 7 i B er 1, så node B’s højre barn vil pege på sig selv. Knude B’s venstre barn vil pege på parent, i dette tilfælde roden. Slutresultatet er vist i figur 9.
Ved at pege knudens B venstre barn til sin forælder muliggør vi den opdeling, der er nævnt i regel nummer 2. Når vi indsætter et tegn, hvis diff falder mellem 2 og 7, vil denne pegepind sende os tilbage til den korrekte position, hvorfra man indsætter det nye tegn. Dette vil ske, når vi indsætter tegn D.
Men før det skal vi indsætte tegn C med en bitkode lig med 01000011. Pointer parent vil pege på node A (roden). Denne gang peger child, anderledes end da vi søgte efter tegn B, på node B (på det tidspunkt pegede begge pointere på roden).
I dette øjeblik gælder uligning (1) (parent.DIFF er mindre end child.DIFF), så vi opdaterer begge pointere, idet vi sætter parent til child og child til node B’s højre child, fordi C’s bit på position 7 er 1.
Efter opdateringen peger begge pointere på node B, hvilket bryder uligning (1). Som vi gjorde før, sammenligner vi child.KEY bitkode med C’s bitkode (01000010 med 01000011) og konkluderer, at de er forskellige ved position 8. Da C’s bit på position 7 er 1, vil denne nye knude (knude C) være højre barn af B. På position 8 er C’s bit 1, hvilket gør, at vi sætter knude C’s højre barn til sig selv, mens dens venstre barn peger på forælder, knude B på dette tidspunkt. Den resulterende trie er i figur 10.

Næste tegn er D (bitkode 01000100). Som vi gjorde med indsættelse af tegn C, vil vi i første omgang sætte pointer parent til node A og pointer child til node B. Uligning (1) er gyldig, så vi opdaterer pointerne. Nu peger parent på node B og child på node B’s venstre child, fordi D’s bit på position 7 er 0. I modsætning til indsættelse af tegn C peger child nu tilbage på node A, hvilket bryder uligning (1). Igen beregner vi forskellen mellem A og D bitkoder. Nu er forskellen 6. Igen indstiller vi parent og child som vi normalt gør. Mens uligning (1) nu er gyldig, er uligning (2) det ikke. Det betyder, at vi indsætter D som venstre barn af A. Men hvad med D’s børn? På position 6 er D’s bit 1, så D’s højre barn peger på sig selv. Det interessante er, at node D’s venstre barn nu vil pege på node B og nå frem til den trie, der er tegnet i figur 11.

Det næste er tegn E med bitkoden 01000101. Search-funktionen returnerer knudepunkt D. Forskellen mellem tegn D og E falder på bit på position 8. Da E’s bit i position 6 er 1, vil den blive placeret til højre for D. Treens struktur er illustreret i figur 12.

Det interessante ved at indsætte tegn F er, at dets plads er mellem tegn D og E, fordi forskellen mellem D og F er på position 7. Men på position 7 er E’s bit 0, så node E vil være venstre barn af node F. Strukturen er nu illustreret i figur 13.

Og til sidst indsætter vi tegn G. Efter alle beregninger konkluderer vi, at det nye knudepunkt skal placeres som højre barn af knudepunkt F med diff lig med 8. Det endelige resultat er i figur 14.

Hertil nu indsætter vi strenge, der kun består af ét tegn. Hvad ville der ske, hvis vi forsøger at indsætte strings AB og BA? Den interesserede læser kan tage dette forslag som en øvelse. To hints: begge strenge adskiller sig fra knude B på position 9, og den endelige trie er illustreret i figur 15.

Tænker man over den sidste figur, kan man stille sig følgende spørgsmål: For at finde f.eks. strengen BA skal man bruge 5 bit-sammenligninger, mens der for at beregne hashkoden for denne streng kun er behov for to iterationer, så hvornår bliver PATRICIA Trie konkurrencedygtig? Forestil dig, at vi i denne struktur indsætter strengen ABBABABABBBBBBBABABBA (taget fra eksemplet i PATRICIA’s oprindelige dokument fra 1968), som er 16 tegn lang? Denne streng ville blive placeret som venstre barn af node AB med diff på position 17. For at finde den ville vi have brug for 5 bit-sammenligninger, mens det ville kræve 16 iterationer at beregne hashkoden, én for hvert tegn, hvilket er grunden til, at PATRICIA Trie er så konkurrencedygtig, når der søges efter lange strenge.
PATRICIA Trie vs Hash Map
I dette sidste afsnit vil jeg sammenligne Hash Map og PATRICIA Trie i to anvendelser. Den første er en ordtælling på leipzig1m.txt, der indeholder 1 million tilfældige sætninger, og den anden er at udfylde en symboltabel med mere end 2,3 millioner URL’er fra DMOZ-projektet (lukket i 2017) hentet herfra.
Den kode, jeg udviklede og brugte til både at implementere pseudokoden ovenfor og sammenligne PATRICIA Trie-ydelsen med Hash Table, kan findes på min GitHub.
Disse sammenligninger blev kørt i min Ubuntu 18.04-boks. Configurantion kan findes i figur 16