WORDER STATA
Markov-switching models
Highlights
- Markov-modelowanie przejściowe
- Model autoregresyjny
- Dynamiczny model regresji
- Parametry regresji zależne od stanu
- Parametry wariancji zależne od stanustep)
- Dynamiczne (multistep)
- RMSE predykcji
O co tu chodzi?
Czasami, procesy ewoluują w czasie z dyskretnymi zmianami w wynikach.
Pomyśl o recesjach i ekspansjach gospodarczych. Na początku recesji, produkcja i zatrudnienie spadają i pozostają na niskim poziomie, a następnie, później, produkcja i zatrudnienie rosną. Pomyśl o zaburzeniach dwubiegunowych, w których występują okresy maniakalne, po których następują okresy depresyjne, a proces się powtarza. Statystycznie rzecz biorąc, średnie, wariancje i inne parametry zmieniają się w różnych epizodach (reżimach). Naszym problemem jest oszacowanie, kiedy zmieniają się reżimy i wartości parametrów związanych z każdym reżimem. Pytanie o to, kiedy reżimy się zmieniają jest równoważne pytaniu o to, jak długo reżimy się utrzymują.
W modelach z przejściem Markowa, oprócz oszacowania średnich, wariancji, itp. każdego reżimu, szacujemy również prawdopodobieństwo zmiany reżimu. Oszacowane prawdopodobieństwa przejścia dla pewnego problemu mogą być, następujące:
| od/do | ||
| stanu | . 1 2 | |
| 1 | 0.82 0,18 | |
| 2 | 0,75 0,25 | |
Start w stanie 1. Prawdopodobieństwo przejścia ze stanu 1 do stanu 1 wynosi 0,82. Innymi słowy, gdy proces znajdzie się w stanie 1, ma tendencję do pozostania w nim. Jednak z prawdopodobieństwem 0,18 proces przechodzi do stanu 2. Stan 2 nie jest tak trwały. Z prawdopodobieństwem 0,75, procesy powracają ze stanu 2 do stanu 1 w następnym okresie czasu.
Modele z przełączaniem Markowa nie są ograniczone do dwóch stanów, chociaż modele dwustanowe są powszechne.
W powyższym przykładzie opisaliśmy przełączanie jako nagłe; prawdopodobieństwo natychmiast się zmieniło. Takie modele Markowa nazywane są modelami dynamicznymi. Modele Markowa mogą również uwzględniać łagodniejsze zmiany poprzez modelowanie prawdopodobieństwa przejścia jako procesu autoregresyjnego.
Tak więc przełączanie może być płynne lub gwałtowne.
Zobaczmy jak to działa
Przyjrzyjmy się średnim zmianom w różnych reżimach. W szczególności, będziemy analizować stopę funduszy federalnych. Federal Funds Rate to stopa procentowa, którą bank centralny Stanów Zjednoczonych pobiera od banków komercyjnych za pożyczki na noc. Przyjrzymy się zmianom stopy funduszy federalnych od 1954 roku do końca 2010 roku. Oto dane:
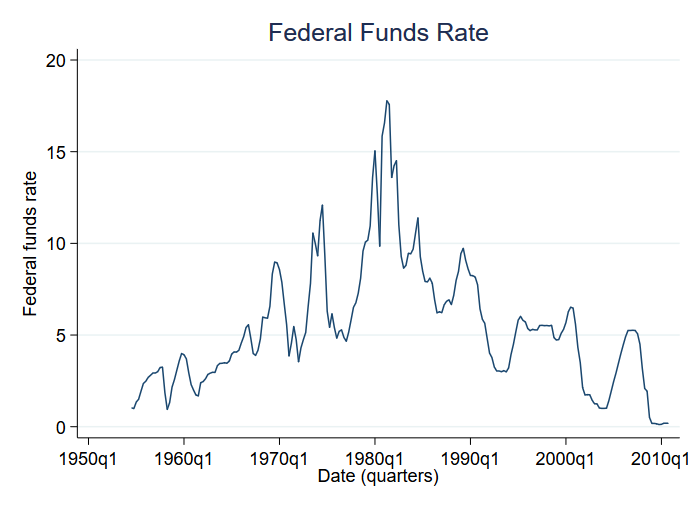
Mamy dane kwartalne. Wysokie stopy procentowe wydają się charakteryzować lata siedemdziesiąte i osiemdziesiąte. Przyjmiemy, że istnieje inny reżim dla niższych stóp procentowych, które wydają się charakteryzować pozostałe dekady.
Aby dopasować model dynamicznej zmiany (abrupt-change) z dwoma reżimami, wpisujemy
. mswitch dr fedfundsPerforming EM optimizaton:Performing gradient-based optimization:
| Iteracja 0: | log likelihood = -508.66031 |
| Iteracja 1: | log likelihood = -508.6382 |
| Iteracja 2: | log likelihood = -508.63592 |
| Iteracja 3: | log likelihood = -508.63592 |
Markov-switching dynamic regressionSample: 1954q3 – 2010q4 No. of obs = 226Number of states = 2 AIC = 4,5455Unconditional probabilities: transition HQIC = 4,5760 SBIC = 4,6211Log likelihood = -508.63592
| fedfunds | Coef. Std. Err. z P>|z| | |
| State1 | ||
| _cons | 3.70877 .1767083 20.99 0.000 3.362428 4.055112 | |
| State2 | ||
| _cons | 9.556793 .2999889 31,86 0,000 8,968826 10,14476 | |
| sigma | 2,107562 .1008692 1,918851 2.314831 | |
| p11 | .9820939 .0104002 .9450805 .9943119 | |
| p21 | .0503587 .0268434 .0173432 .1374344 | |
W powyższych danych wyjściowych znajdują się
- średnie dwóch stanów (_cons);
- pojedyncze odchylenie standardowe dla całego procesu (sigma); oraz
- prawdopodobieństwa przejścia ze stanu 1 do 1 i ze stanu 2 do 1 (p11 i p21).
Stan1 jest stanem o umiarkowanej szybkości (średnia 3,71%).
Stan2 jest stanem wysokim (średnia 9,56%).
| od/do | ||
| stanu | . 1 2 | |
| 1 | 0.98 1 – 0,98 | |
| 2 | 0,05 1 – 0,05 | |
Oba stany są niesamowicie trwałe (prawdopodobieństwa 1->1 i 2->2 równe 0,98 i 0,95).
Wśród rzeczy, które można przewidzieć po estymacji jest prawdopodobieństwo bycia w różnych stanach. Mamy tylko dwa stany, a zatem prawdopodobieństwo bycia w (powiedzmy) stanie 2 mówi nam o prawdopodobieństwie dla obu stanów. Możemy uzyskać przewidywane prawdopodobieństwo i wykreślić je wraz z oryginalnymi danymi:
. predict prfed, pr
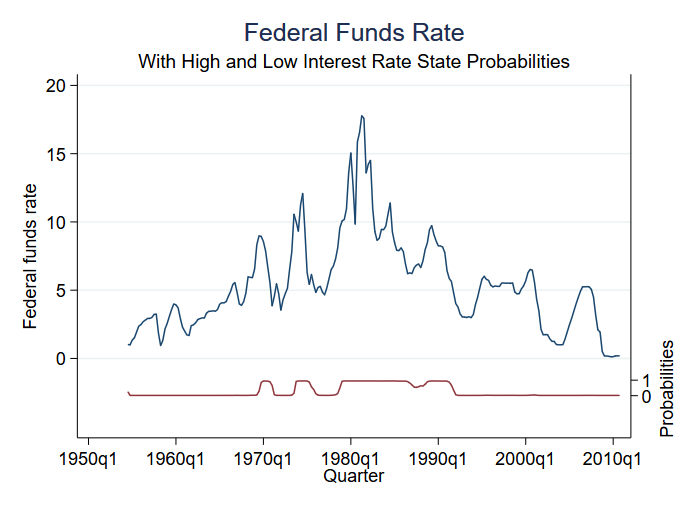
Model ma małą niepewność co do reżimu w każdym punkcie w czasie. Widzimy trzy okresy stanów wysokich i cztery okresy stanów umiarkowanych.
Zobaczmy jak to działa
Spójrzmy na przykład wybuchu choroby, mianowicie świnki na 10,000 mieszkańców w Nowym Jorku między 1929 a 1972. Można by pomyśleć, że epidemie odpowiadają zmianom średniej, ale to, co widzimy w danych, to jeszcze większa zmiana wariancji:
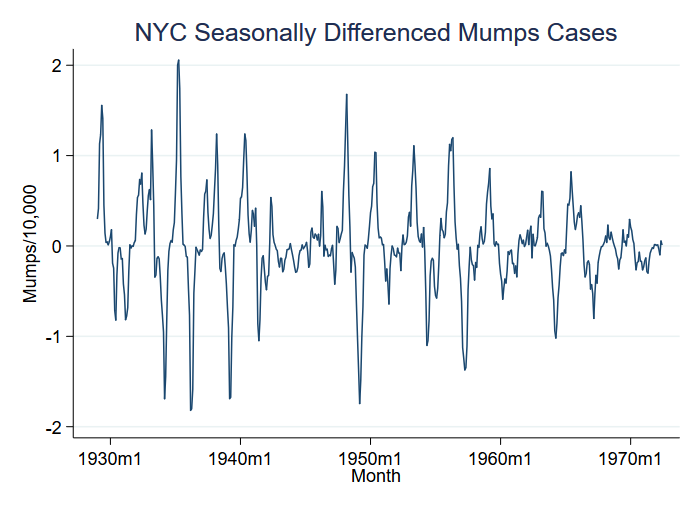
Wykreśliliśmy zmienną S12.mumpspc, oznaczającą sezonowo zróżnicowane przypadki świnki na mieszkańca w okresie 12 miesięcy, i będziemy analizować S12.mumpspc.
Zamierzamy założyć dwa reżimy, w których średnia i wariancja S12.mumpspc zmieniają się. Aby dopasować model dynamiczny (abrupt-change), wpisujemy
. mswitch dr S12.mumpspc, varswitch switch(LS12.mumpspc, noconstant)Performing EM optimizaton:Performing gradient-based optimization:
| Iteracja 0: | log likelihood = 110.9372 (nie wklęsły) |
| Iteracja 1: | log likelihood = 120.68028 |
| Iteracja 2: | log likelihood = 123.23244 |
| Iteracja 3: | log likelihood = 131.47084 |
| Iteracja 3: | log likelihood = 131.72182 |
| Iteracja 3: | log likelihood = 131.7225 |
| Iteracja 3: | log likelihood = 131.7225 |
Markov-switching dynamic regressionSample: 1929m2 – 1972m6 No. of obs = 521Number of states = 2 AIC = -0.4826Unconditional probabilities: transition HQIC = -0.4634 SBIC = -0.4336Log likelihood = 131.7225
| S12.mumspc | Coef. Std. Err. z P>|z| | |
| State1 | ||
| mumpspc | ||
| LS12. | .4202751 .0167461 25.10 0.000 .3874533 .4530968 | |
| State2 | ||
| mumpspc | ||
| LS12. | .9847369 .0258383 38.11 0.000 .9340947 1.035379 | |
| sigma1 | .0562405 .0050954 .0470901 .067169 | |
| sigma2 | .2611362 .0111191 .2402278 .2838644 | |
| p11 | .762733 .0362619 .6846007 .8264175 | |
| p12 | .1473767 .0257599 .1036675 .205294 | |
Reported are
- the means of the two states of S12.mumpspc (0,42 i 0,98);
- odchylenia standardowe tych dwóch stanów (0,06 i 0,26); oraz
- prawdopodobieństwa przejścia ze stanu 1 do 1 i ze stanu 2 do 1 (0,76 i 0,15).
Stan 1 jest stanem o niskiej wariancji.
Pełny zbiór prawdopodobieństw przejścia jest następujący: