Pierwszy wykres powyżej pokazuje, że większe rozmiary partii rzeczywiście pokonują mniejszą odległość na epokę. Odległość epokowa dla partii 32 waha się od 0.15 do 0.4, podczas gdy dla partii 256 wynosi około 0.02-0.04. W rzeczywistości, jak widać na drugim wykresie, stosunek odległości epok rośnie z czasem!
Ale dlaczego szkolenie w dużych partiach pokonuje mniejszą odległość na epokę? Czy to dlatego, że mamy mniej partii, a zatem mniej aktualizacji na epokę? Czy może dlatego, że każda aktualizacja partii pokonuje mniejszą odległość? Czy może odpowiedź jest kombinacją obu tych czynników?
Aby odpowiedzieć na to pytanie, zmierzmy rozmiar każdej aktualizacji partii.

Median batch update norm for batch size 32: 3.3e-3
Median batch update norm for batch size 256: 1.5e-3
Widzimy, że każda aktualizacja partii jest mniejsza, gdy rozmiar partii jest większy. Dlaczego tak się dzieje?
Aby zrozumieć to zachowanie, załóżmy fikcyjny scenariusz, w którym mamy dwa wektory gradientu a i b, każdy reprezentujący gradient dla jednego przykładu szkoleniowego. Zastanówmy się, jak średnia wielkość aktualizacji partii dla partii o rozmiarze=1 porównuje się do tej z partii o rozmiarze=2.

Jeśli użyjemy wielkości partii równej jeden, zrobimy krok w kierunku a, następnie b, kończąc w punkcie reprezentowanym przez a+b. (Technicznie rzecz biorąc, gradient dla b zostałby ponownie obliczony po zastosowaniu a, ale na razie zignorujmy to). Wynikiem tego jest średni rozmiar aktualizacji wsadu wynoszący (|a|+|b|)/2 – suma rozmiarów aktualizacji wsadu podzielona przez liczbę aktualizacji wsadu.
Jednakże, jeśli użyjemy rozmiaru wsadu równego dwa, aktualizacja wsadu jest zamiast tego reprezentowana przez wektor (a+b)/2 – czerwona strzałka na rysunku 12. Zatem średni rozmiar aktualizacji partii wynosi |(a+b)/2| / 1 = |a+b|/2.
Porównajmy teraz dwa średnie rozmiary aktualizacji partii:

W ostatnim wierszu użyliśmy nierówności trójkąta, aby pokazać, że średni rozmiar aktualizacji partii dla partii o rozmiarze 1 jest zawsze większy lub równy rozmiarowi partii o rozmiarze 2.
Ujmując to inaczej, aby średni rozmiar aktualizacji partii dla partii o rozmiarze 1 i partii o rozmiarze 2 był równy, wektory a i b muszą być skierowane w tym samym kierunku, ponieważ wtedy |a| + |b| = |a+b|. Możemy rozszerzyć ten argument na n wektorów – tylko wtedy, gdy wszystkie n wektorów jest skierowanych w tym samym kierunku, średnie wielkości aktualizacji partii dla wielkości partii=1 i wielkości partii=n są takie same. Jednak prawie nigdy nie ma to miejsca, ponieważ jest mało prawdopodobne, aby wektory gradientu wskazywały dokładnie ten sam kierunek.

Jeśli wrócimy do równania aktualizacji minibatch na rysunku 16, to w pewnym sensie mówimy, że w miarę zwiększania rozmiaru partii |B_k|, wielkość sumy gradientów skaluje się stosunkowo mniej szybko. Wynika to z faktu, że wektory gradientu wskazują różne kierunki, a zatem podwojenie wielkości partii (tj. liczby wektorów gradientu do zsumowania) nie powoduje podwojenia wielkości wynikowej sumy wektorów gradientu. W tym samym czasie dzielimy przez mianownik |B_k|, który jest dwa razy większy, co skutkuje mniejszym krokiem aktualizacji.
To mogłoby wyjaśnić, dlaczego aktualizacje partii dla większych rozmiarów partii mają tendencję do bycia mniejszymi – suma wektorów gradientu staje się większa, ale nie może w pełni skompensować większego mianownika|B_k|.
Hipoteza 2: Trening małoseryjny znajduje bardziej płaskie minimalizatory
Zmierzmy teraz ostrość obu minimalizatorów i oceńmy twierdzenie, że trening małoseryjny znajduje bardziej płaskie minimalizatory. (Zauważmy, że ta druga hipoteza może współistnieć z pierwszą – nie wykluczają się one wzajemnie). W tym celu zapożyczamy dwie metody od Keskara i in.
W pierwszej z nich wykreślamy stratę szkoleniową i walidacyjną wzdłuż linii pomiędzy minimalizatorem dla małej partii (wielkość partii 32) a minimalizatorem dla dużej partii (wielkość partii 256). Linia ta jest opisana następującym równaniem:

where x_l* is the large batch minimizer and x_s* is the small batch minimizer, and alpha is a coefficient between -1 and 2.

Jak widać na wykresie, minimalizator małej partii (alfa=0) jest znacznie bardziej płaski niż minimalizator dużej partii (alfa=1), który zmienia się znacznie ostrzej.
Zauważ, że jest to dość uproszczony sposób pomiaru ostrości, ponieważ uwzględnia tylko jeden kierunek. Dlatego Keskar i inni proponują metrykę ostrości, która mierzy, jak bardzo funkcja straty zmienia się w sąsiedztwie wokół minimalizatora. Najpierw definiujemy sąsiedztwo w następujący sposób:

where epsilon is a parameter defining the size of the neighborhood and x is the minimizer (the weights).
Potem definiujemy metrykę ostrości jako maksymalną stratę w tym sąsiedztwie wokół minimalizatora:

where f is the loss function, with the inputs being the weights.
Mając powyższe definicje, obliczmy ostrość minimalizatorów przy różnych rozmiarach partii, z wartością epsilon równą 1e-3:
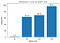
To pokazuje, że minimalizatory dużych partii są rzeczywiście ostrzejsze, jak widzieliśmy na wykresie interpolacji.
Na koniec spróbujmy wykreślić minimalizatory za pomocą wizualizacji straty znormalizowanej przez filtr, jak to sformułowali Li et al . Ten typ wykresu wybiera dwa losowe kierunki o takich samych wymiarach jak wagi modelu, a następnie normalizuje każdy filtr konwolucyjny (lub neuron, w przypadku warstw FC), aby miał taką samą normę jak odpowiadający mu filtr w wagach modelu. Zapewnia to, że na ostrość minimalizatora nie mają wpływu wielkości jego wag. Następnie wykreśla stratę wzdłuż tych dwóch kierunków, przy czym środek wykresu jest minimalizatorem, który chcemy scharakteryzować.