Multiplekser

Multiplekser jest układem kombinacyjnym, który ma 2n linii wejściowych i jedną linię wyjściową. Po prostu, multiplekser jest multi-wejście i pojedynczy obwód wyjściowy combinational. Informacja binarna jest odbierana z linii wejściowych i kierowana do linii wyjściowej. Na podstawie wartości linii wyboru, jedno z tych wejść danych zostanie podłączone do wyjścia.

W przeciwieństwie do kodera i dekodera, istnieje n linii wyboru i 2n linii wejściowych. Tak więc, istnieje w sumie 2N możliwych kombinacji wejść. Multiplekser jest również traktowany jako Mux.

Istnieją różne typy multipleksera, które są następujące:

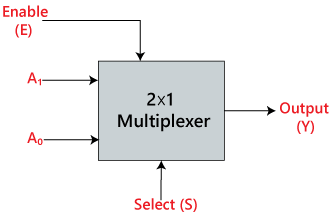
2×1 Multiplekser:

W multiplekserze 2×1 są tylko dwa wejścia, tj, A0 i A1, 1 linia wyboru, tj. S0 i jedno wyjście, tj. Y. Na podstawie kombinacji wejść, które są obecne na linii wyboru S0, jedno z tych 2 wejść zostanie podłączone do wyjścia. Schemat blokowy i tablica prawdy multipleksera 2×1 są podane poniżej.

Schemat blokowy:

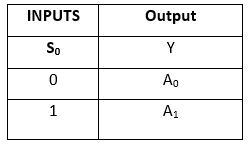
Tablica prawdy:

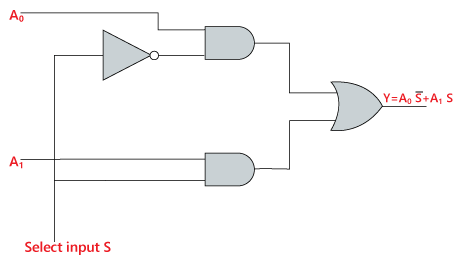
Wyrażenie logiczne wyrażenia Y jest następujące:

Y=S0′.A0+S0.A1

Obwód logiczny powyższego wyrażenia jest podany poniżej:

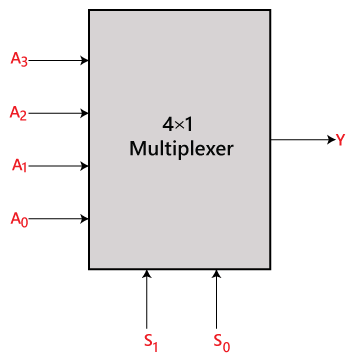
4×1 Multiplekser:

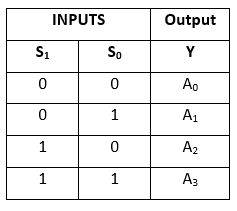
W multiplekserze 4×1 mamy w sumie cztery wejścia, czyli, A0, A1, A2 i A3, 2 linie wyboru, tj. S0 i S1 oraz pojedyncze wyjście, tj. Y. Na podstawie kombinacji wejść, które są obecne na liniach wyboru S0 i S1, jedno z tych 4 wejść jest podłączane do wyjścia. Schemat blokowy i tablica prawdy multipleksera 4×1 są podane poniżej.

Schemat blokowy:

Tablica prawdy:

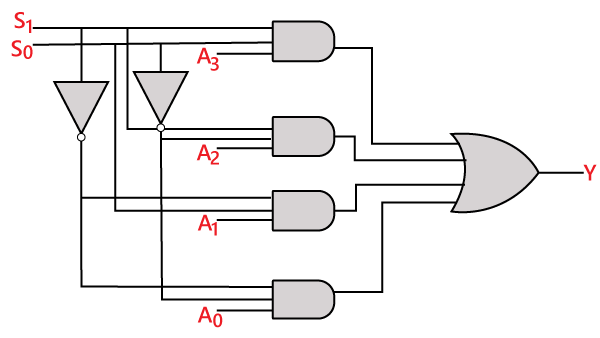
Wyrażenie logiczne terminu Y jest następujące:

Y=S1′ S0′ A0+S1′ S0 A1+S1 S0′ A2+S1 S0 A3

Obwód logiczny powyższego wyrażenia jest podany poniżej:

Multiplekser 8 do 1

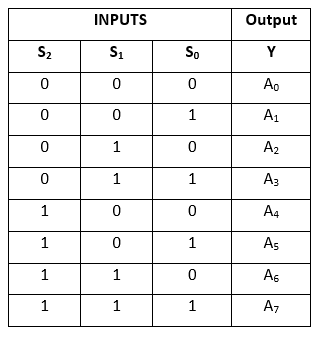
W multiplekserze 8 do 1 jest łącznie osiem wejść, tj.e., A0, A1, A2, A3, A4, A5, A6 i A7, 3 linie wyboru, tj. S0, S1 i S2 oraz jedno wyjście, tj. Y. Na podstawie kombinacji wejść, które są obecne na liniach wyboru S0, S1 i S2, jedno z tych 8 wejść jest podłączone do wyjścia. Schemat blokowy i tablica prawdy multipleksera 8×1 są podane poniżej.

Schemat blokowy:

Tablica prawdy:

Wyrażenie logiczne wyrażenia Y jest następujące:

Y=S0′.S1′.S2′.A0+S0.S1′.S2′.A1+S0′.S1.S2′.A2+S0.S1.S2′.A3+S0′.S1′.S2 A4+S0.S1′.S2 A5+S0′.S1.S2 .A6+S0.S1.S3.A7

Obwód logiczny powyższego wyrażenia jest podany poniżej:

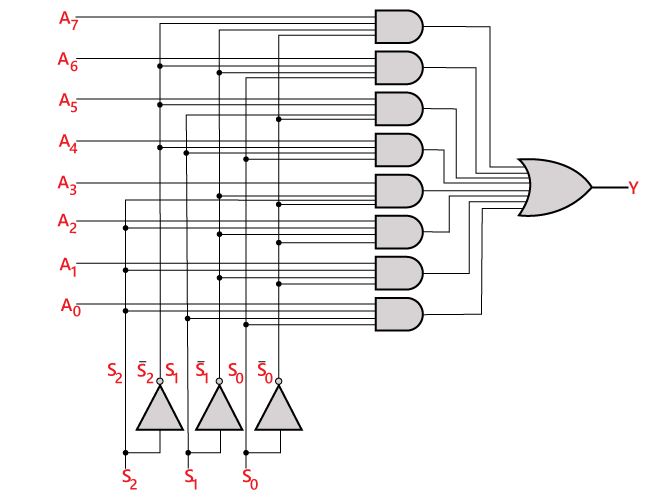
8 ×1 multiplekser z wykorzystaniem multipleksera 4×1 i 2×1

Możemy zaimplementować multiplekser 8×1 z wykorzystaniem multipleksera niższego rzędu. Aby zaimplementować multiplekser 8×1, potrzebujemy dwóch multiplekserów 4×1 i jednego multipleksera 2×1. Multiplekser 4×1 ma 2 linie wyboru, 4 wejścia i 1 wyjście. Multiplekser 2×1 ma tylko 1 linię selekcji.

Aby uzyskać 8 wejść danych, potrzebujemy dwóch multiplekserów 4×1. Multiplekser 4×1 wytwarza jedno wyjście. Tak więc, aby uzyskać ostateczne wyjście, potrzebujemy multipleksera 2×1. Schemat blokowy multipleksera 8×1 z wykorzystaniem multipleksera 4×1 i 2×1 jest podany poniżej.

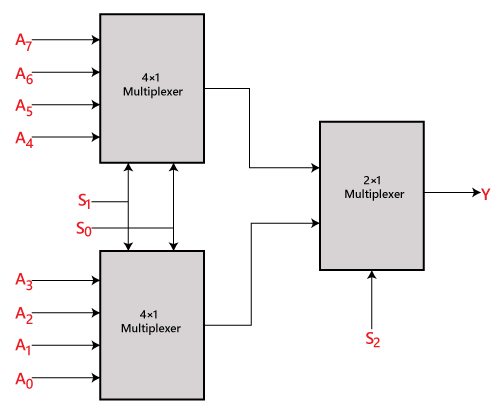
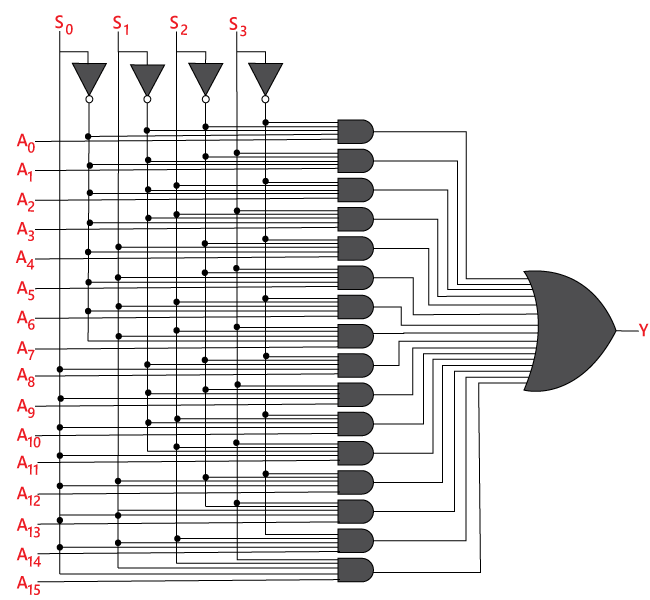
Multiplekser 16 do 1

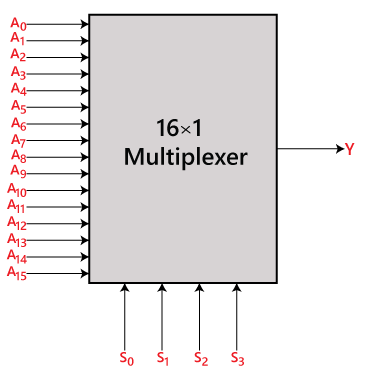
W multiplekserze 16 do 1 jest łącznie 16 wejść, tj., A0, A1, …, A16, 4 linie selekcji, tj., S0, S1, S2 i S3 oraz jedno wyjście, tj. Y. Na podstawie kombinacji wejść, które znajdują się na liniach selekcyjnych S0, S1 i S2, jedno z tych 16 wejść zostanie podłączone do wyjścia. Schemat blokowy i tabela prawdy układu 16×1

Schemat blokowy:

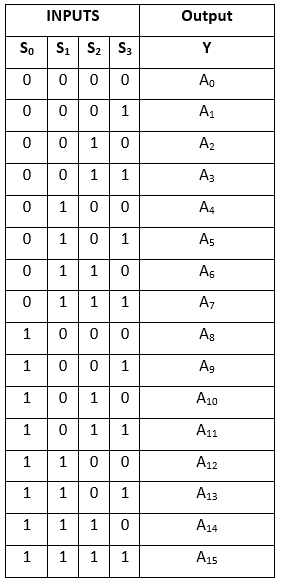
Tablica prawdy:

Wyrażenie logiczne terminu Y jest następujące:

Obwód logiczny powyższego wyrażenia jest podany poniżej:

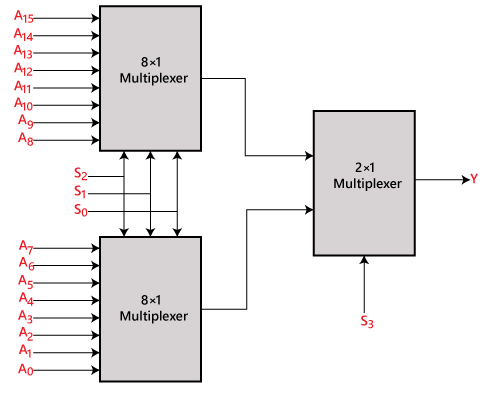
Multiplekser 16×1 z wykorzystaniem multipleksera 8×1 i 2×1

Możemy zaimplementować multiplekser 16×1 z wykorzystaniem multipleksera niższego rzędu. Aby zaimplementować multiplekser 8×1, potrzebujemy dwóch multiplekserów 8×1 i jednego multipleksera 2×1. Multiplekser 8×1 ma 3 linie wyboru, 4 wejścia i 1 wyjście. Multiplekser 2×1 ma tylko 1 linię selekcji.

Aby uzyskać 16 wejść danych, potrzebujemy dwóch multiplekserów 8×1. Multiplekser 8×1 wytwarza jedno wyjście. Tak więc, aby uzyskać ostateczne wyjście, potrzebujemy multipleksera 2×1. Schemat blokowy multipleksera 16×1 z wykorzystaniem multipleksera 8×1 i 2×1 jest podany poniżej.