ORDER STATA
Markovovy-přepínací modely
Highlights
- Markov-přechodové modelování
- Autoregresní model
- Dynamický regresní model
- Regresní parametry závislé na stavu
- Stát-závislé rozptylové parametry
- Tabulky
- Pravděpodobnosti přechodu
- Očekávané doby trvání stavu
- Předpovědi
- Očekávané hodnoty závislé proměnné
- Pravděpodobnosti pobytu ve stavu
- Statické (jedno-krok)
- Dynamické (vícekrokové)
- RMSE předpovědí
O co jde?
Někdy se procesy vyvíjejí v čase s diskrétními změnami výsledků.
Vzpomeňte si na hospodářské recese a expanze. Na počátku recese produkce a zaměstnanost klesají a zůstávají nízké, později se produkce a zaměstnanost zvyšují. Přemýšlejte o bipolárních poruchách, při nichž se střídají manická období s depresivními obdobími a proces se opakuje. Statisticky se střední hodnoty, rozptyly a další parametry v jednotlivých epizodách (režimech) mění. Naším problémem je odhadnout, kdy se režimy mění, a hodnoty parametrů spojených s jednotlivými režimy. Otázka, kdy se režimy mění, je ekvivalentní otázce, jak dlouho režimy přetrvávají.
V markovovských přechodových modelech kromě odhadu středních hodnot, rozptylů atd. každého režimu odhadujeme také pravděpodobnost změny režimu. Odhadované pravděpodobnosti přechodu pro nějaký problém mohou být, následující:
| z/do | |||
| stavu | . 1 2 | ||
| 1 | 0.82 0,18 | ||
| 2 | 0,75 0,25 | ||
Začněte ve stavu 1. Pravděpodobnost přechodu ze stavu 1 do stavu 1 je 0,82. Jinak řečeno, jakmile se proces dostane do stavu 1, má tendenci v něm zůstat. S pravděpodobností 0,18 však proces přechází do stavu 2. Stav 2 není tak trvalý. S pravděpodobností 0,75 se procesy v následujícím časovém období vrátí ze stavu 2 do stavu 1.
Markovovy přepínací modely nejsou omezeny na dva režimy, i když dvourežimové modely jsou běžné.
Ve výše uvedeném příkladu jsme přepnutí popsali jako náhlé; pravděpodobnost se okamžitě změnila. Takové Markovovy modely se nazývají dynamické modely. Markovovy modely mohou zohledňovat i plynulejší změny tím, že pravděpodobnosti přechodu modelují jako autoregresní proces.
Přepínání tedy může být plynulé nebo náhlé.
Podívejme se, jak to funguje
Podívejme se na průměrné změny napříč režimy. Konkrétně budeme analyzovat sazbu federálních fondů. Sazba federálních fondů je úroková sazba, kterou centrální banka USA účtuje komerčním bankám za jednodenní úvěry. Budeme se zabývat změnami sazby federálních fondů od roku 1954 do konce roku 2010. Zde jsou údaje:
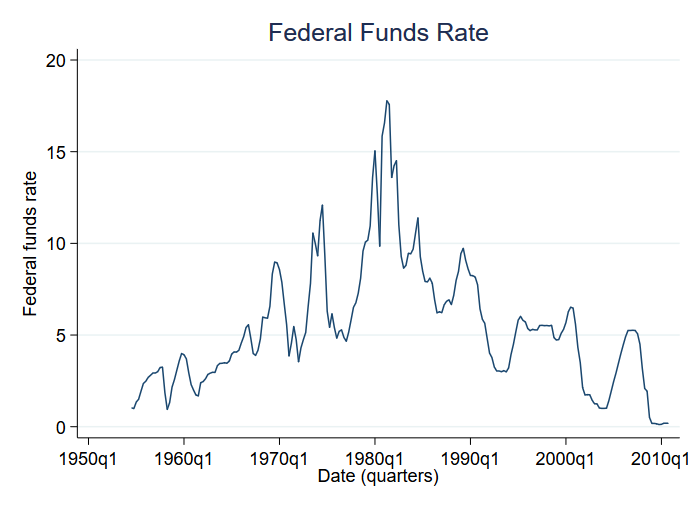
Máme k dispozici čtvrtletní údaje. Zdá se, že vysoké úrokové sazby charakterizují sedmdesátá a osmdesátá léta. Budeme předpokládat, že existuje jiný režim pro nižší úrokové sazby, které zřejmě charakterizují ostatní desetiletí.
Pro fitování modelu s dynamickým přepínáním (náhlou změnou) se dvěma režimy zadáme
. mswitch dr fedfundsPerforming EM optimizaton:Performing gradient-based optimization:
| Iterace 0: | log likelihood = -508.66031 |
| Iterace 1: | log likelihood = -508,6382 |
| Iterace 2: | log likelihood = -508.63592 |
| Iterace 3: | log likelihood = -508,63592 |
Markovova dynamická regreseSample: 1954q3 – 2010q4 No. of obs = 226Number states = 2 AIC = 4,5455Unconditional probabilities: transition HQIC = 4,5760 SBIC = 4,6211Log likelihood = -508.63592
| fedfunds | Coef. Std. chyba z P>|z| | ||
| Stát1 | |||
| _cons | 3.70877 .1767083 20.99 0.000 3.362428 4.055112 | ||
| Stav2 | |||
| _cons | 9.556793 .2999889 31,86 0,000 8,968826 10,14476 | ||
| sigma | 2,107562 .1008692 1,918851 2.314831 | ||
| p11 | .9820939 .0104002 .9450805 .9943119 | ||
| p21 | .0503587 .0268434 .0173432 .1374344 | ||
Ve výše uvedeném výstupu jsou uváděny
- střední hodnoty obou stavů (_cons);
- jediná směrodatná odchylka pro celý proces (sigma); a
- pravděpodobnosti přechodu ze stavu 1 na 1 a ze stavu 2 na 1 (p11 a p21).
Stav1 je stav se střední mírou (průměr 3,71 %).
Stav2 je stav s vysokou mírou pravděpodobnosti (průměr 9,56 %).
| z/do | ||
| stát | . 1 2 | |
| 1 | 0.98 1 – 0,98 | |
| 2 | 0,05 1 – 0,05 | |
Oba stavy jsou neuvěřitelně trvalé (1->1 a 2->2 pravděpodobnosti 0,98 a 0,95).
Mezi věci, které můžete po odhadu předpovědět, patří pravděpodobnost, že se budete nacházet v různých stavech. Máme pouze dva stavy, a tak pravděpodobnost, že se nacházíme (řekněme) ve stavu 2, nám říká pravděpodobnost pro oba stavy. Předpovězenou pravděpodobnost můžeme získat a vynést ji do grafu spolu s původními daty:
. predict prfed, pr
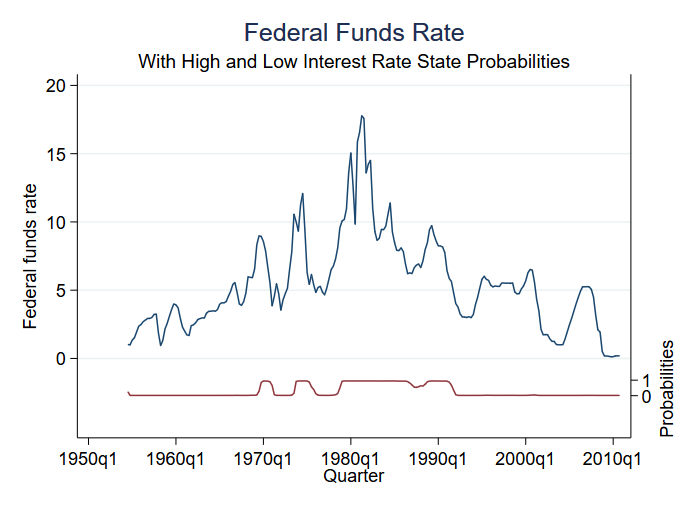
Model má malou nejistotu ohledně režimu v každém časovém okamžiku. Vidíme tři období stavů s vysokou rychlostí a čtyři období stavů se střední rychlostí.
Podívejme se, jak to funguje
Podívejme se na příklad výskytu nemoci, konkrétně příušnic na 10 000 obyvatel v New Yorku v letech 1929 až 1972. Mohli byste si myslet, že epidemie odpovídají průměrným změnám, ale v datech vidíme ještě větší změnu rozptylu:
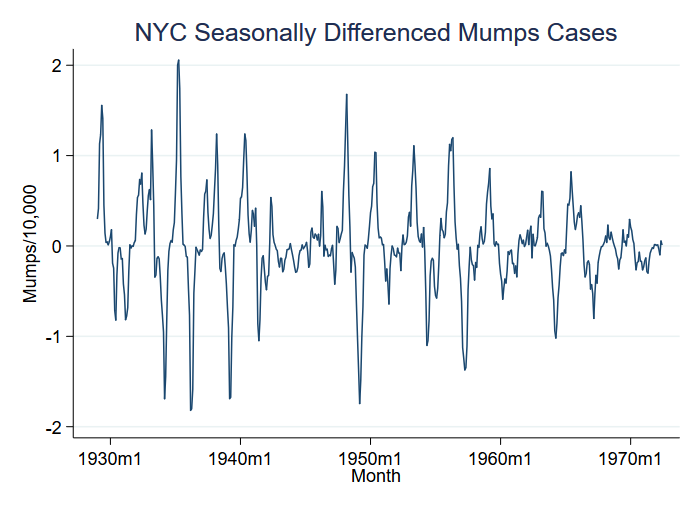
Do grafu jsme zakreslili proměnnou S12.mumpspc, což znamená sezónně diferencované případy příušnic na obyvatele za období 12 měsíců, a budeme analyzovat S12.mumpspc.
Budeme předpokládat dva režimy, ve kterých se mění průměr a rozptyl S12.mumpspc. Pro fitování dynamického modelu (s náhlou změnou) zadáme
. mswitch dr S12.mumpspc, varswitch switch(LS12.mumpspc, noconstant)Performing EM optimizaton:Performing gradient-based optimization:
| Iterace 0: | log likelihood = 110,9372 (není konkávní) |
| Iterace 1: | log likelihood = 120.68028 |
| Iterace 2: | log likelihood = 123,23244 |
| Iterace 3: | log likelihood = 131,47084 |
| Iterace 3: | log likelihood = 131.72182 |
| Iterace 3: | log likelihood = 131,7225 |
| Iterace 3: | log likelihood = 131,7225 |
Markovova dynamická regreseSample: 1929m2 – 1972m6 No. of obs = 521Number states = 2 AIC = -0,4826Unconditional probabilities: transition HQIC = -0,4634 SBIC = -0,4336Log likelihood = 131,7225
| S12.mumspc | Coef. Std. chyba z P>|z| | |
| State1 | ||
| mumpspc | ||
| LS12. | .4202751 .0167461 25.10 0.000 .3874533 .4530968 | |
| Stát2 | ||
| mumpspc | ||
| LS12. | .9847369 .0258383 38.11 0.000 .9340947 1.035379 | |
| sigma1 | .0562405 .0050954 .0470901 .067169 | |
| sigma2 | .2611362 .0111191 .2402278 .2838644 | |
| p11 | .762733 .0362619 .6846007 .8264175 | |
| p12 | .1473767 .0257599 .1036675 .205294 | |
Uváděny jsou
- střední hodnoty dvou stavů S12.mumpspc (0,42 a 0,98);
- směrodatné odchylky obou stavů (0,06 a 0,26) a
- pravděpodobnosti přechodu ze stavu 1 do stavu 1 a ze stavu 2 do stavu 1 (0,76 a 0,15).
Stav 1 je stav s nízkou odchylkou.
Úplný soubor pravděpodobností přechodu je následující: