Percentil je místo v rozdělení, které má určitou část (nebo procento) rozdělení „pod sebou“ (vlevo). Jinými slovy, pokud je #n^“th „# percentil #x# a my z rozdělení vylosujeme náhodné číslo #X#, pak šance, že #X# bude menší než #x#, je #n %#:
#n^“th“ “ percentil“ = x“ „#means#“ “ P(X < x)=n%.#
Například u standardní normální křivky (s #mu = 0# a #sigma = 1#) je bod, kde #x=0# (tj. osa #y#) je 50. percentil, protože 50 % plochy křivky připadá vlevo od #x=0#:

Standardní normální rozdělení #Z# je tak dobrý základ, že vlastně máme tabulku hodnot určenou speciálně pro vyhledávání percentilů pro tuto křivku. Říká se jí tabulka #z# a vypadá nějak takto:
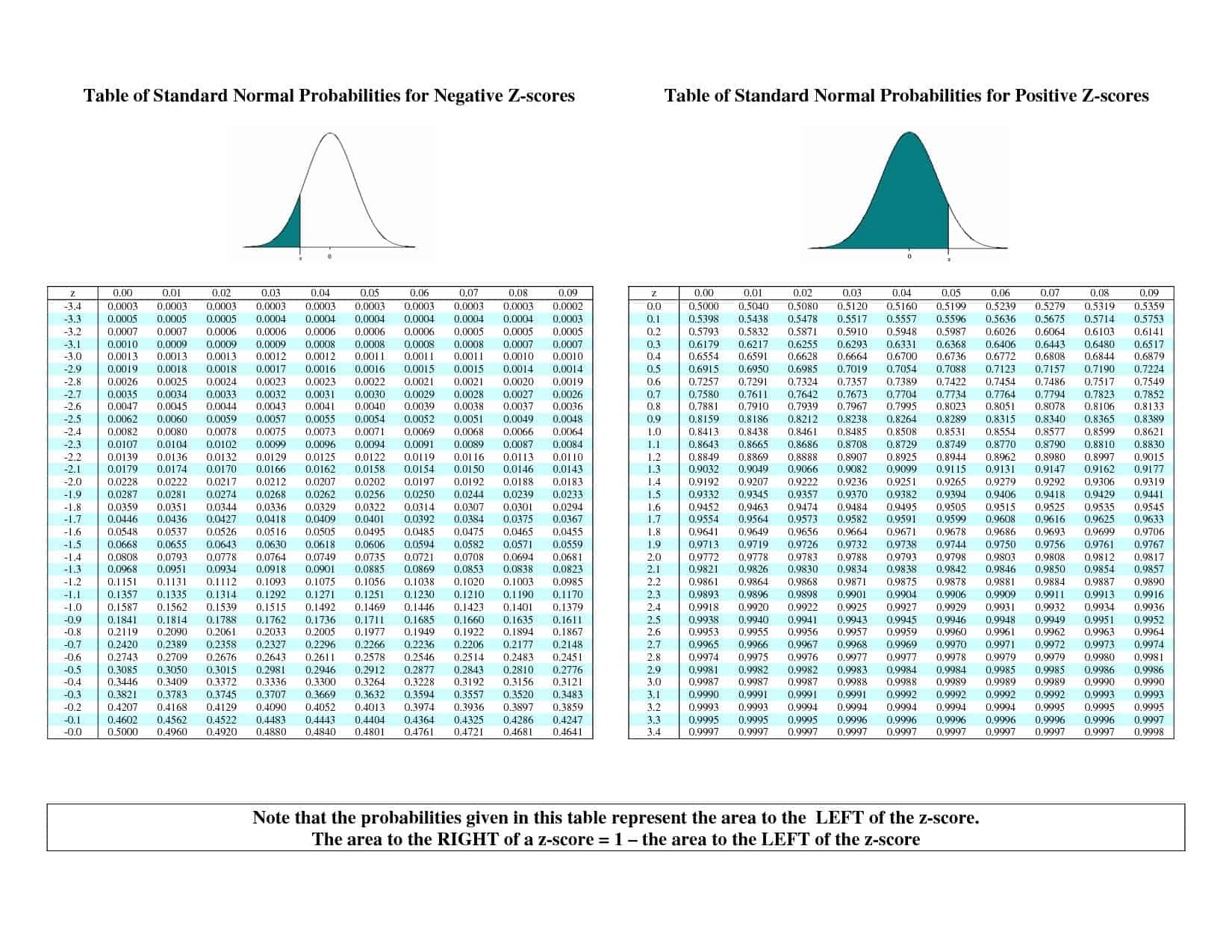
Jak ji používáme? Řekněme, že chceme 25. percentil pro standardní normální rozdělení. Najdeme v tabulce hodnotu nejbližší 0,25 (což je shodou okolností 0,2514) a zjistíme, že se nachází v řádku #“-„0,6# a sloupci #0,07#. Pro tuto tabulku to znamená, že 25. percentil je (přibližně) #“-„0,67#.
Ale počkat – jak nám to pomůže, když chceme percentil pro jakékoli normální rozdělení #X#? Potřebujeme najít souvislost mezi libovolnou křivkou a standardní normální křivkou. Tuto souvislost nalezneme tak, že rozdělení #X# posuneme zleva doprava tak, aby mělo střed v bodě #0#, a pak ho protáhneme/rozšíříme tak, aby jeho směrodatná odchylka byla #1#. Vzorec pro to je:
#Z=(X-mu)/sigma#
kde #mu# je střední hodnota #X# a #sigma# je s.d. #X#.
Známe-li požadovaný percentil z rozdělení #Z#, můžeme řešit #X# přeuspořádáním rovnice na
#X=sigma Z + mu#.
Použijme jako příklad první otázku, kterou jste položil, kde #X# je normálně rozdělený s #mu = 81,2# a #sigma = 12,4# a my hledáme 16. percentil.
Z výše uvedené tabulky je 16. percentil z rozdělení #Z# přibližně #“-„0,99#. Ekvivalentní umístění v našem rozdělení #X# je pak:
#X=(12,4)(„-„0,99)+81,2#
#color(white)X=“-„12,276+81.2#
#color(white)X=68.924#
Co to říká: jestliže #X# je normální křivka s #mu=81.2 “ nohou „# a #sigma=12.4 “ stop „#, pak je 16% šance, že pozorování z #X# bude menší než #68,924 “ stop „#.
Zbytek nechám na vás jako cvičení; s výše uvedenými vzorci by to nemělo být tak těžké.
Doufám, že to pomohlo!