Multiplexer

Multiplexer je kombinační obvod, který má 2n vstupních linek a jednu výstupní linku. Zjednodušeně řečeno, multiplexor je kombinační obvod s více vstupy a jedním výstupem. Binární informace jsou přijímány ze vstupních linek a směrovány na výstupní linku. Na základě hodnot selekčních linek se jedna z těchto vstupních dat připojí k výstupu.

Na rozdíl od kodéru a dekodéru existuje n selekčních linek a 2n vstupních linek. Existuje tedy celkem 2N možných kombinací vstupů. Multiplexer je také považován za Mux.

Existují různé typy multiplexerů, které jsou následující:

2×1 Multiplexer:

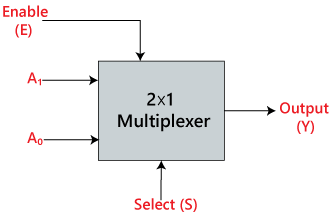
V multiplexeru 2×1 jsou pouze dva vstupy, tj, A0 a A1, 1 selekční linka, tj. S0, a jediný výstup, tj. Y. Na základě kombinace vstupů, které jsou přítomny na selekční lince S0, bude jeden z těchto 2 vstupů připojen na výstup. Blokové schéma a pravdivostní tabulka multiplexoru 2×1 jsou uvedeny níže.

Blokové schéma:

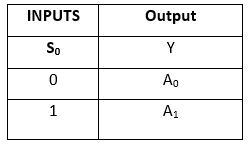
Pravdivostní tabulka:

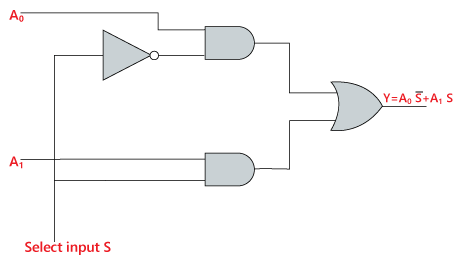
Logické vyjádření členu Y je následující:

Y=S0′.A0+S0.A1

Logický obvod výše uvedeného výrazu je uveden níže:

4×1 multiplexor:

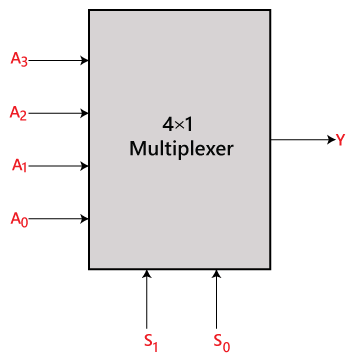
V multiplexoru 4×1 jsou celkem čtyři vstupy, tj, A0, A1, A2 a A3, 2 selekční linky, tj. linky S0 a S1, a jediný výstup, tj. výstup Y. Na základě kombinace vstupů, které jsou přítomny na selekčních linkách S0 a S1, je jeden z těchto 4 vstupů připojen na výstup. Blokové schéma a pravdivostní tabulka multiplexoru 4×1 jsou uvedeny níže.

Blokové schéma:

Pravdivostní tabulka:

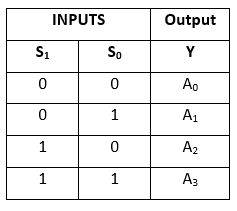
Logické vyjádření členu Y je následující:

Y=S1′ S0′ A0+S1′ S0 A1+S1 S0′ A2+S1 S0 A3

Logické zapojení výše uvedeného výrazu je uvedeno níže:

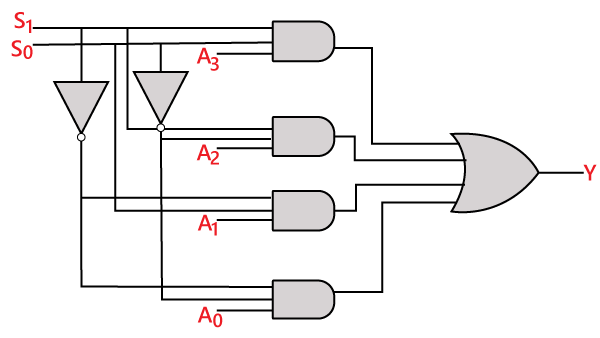
8 až 1 multiplexor

V multiplexoru 8 až 1 je celkem osm vstupů, tj.e., A0, A1, A2, A3, A4, A5, A6 a A7, 3 selekční linky, tj. S0, S1a S2, a jediný výstup, tj. výstup Y. Na základě kombinace vstupů, které jsou přítomny na selekčních linkách S0, S1 a S2, je jeden z těchto 8 vstupů připojen na výstup. Blokové schéma a pravdivostní tabulka multiplexoru 8×1 jsou uvedeny níže.

Blokové schéma:

Pravdivostní tabulka:

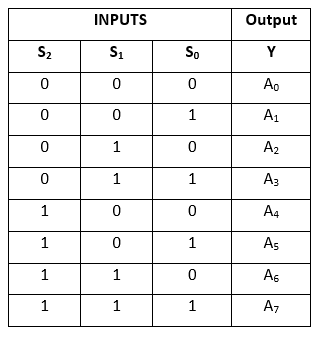
Logické vyjádření členu Y je následující:

Y=S0′.S1′.S2′.A0+S0.S1′.S2′.A1+S0′.S1.S2′.A2+S0.S1.S2′.A3+S0′.S1′.S2 A4+S0.S1′.S2 A5+S0′.S1.S2 .A6+S0.S1.S3.A7

Logické zapojení výše uvedeného výrazu je uvedeno níže:

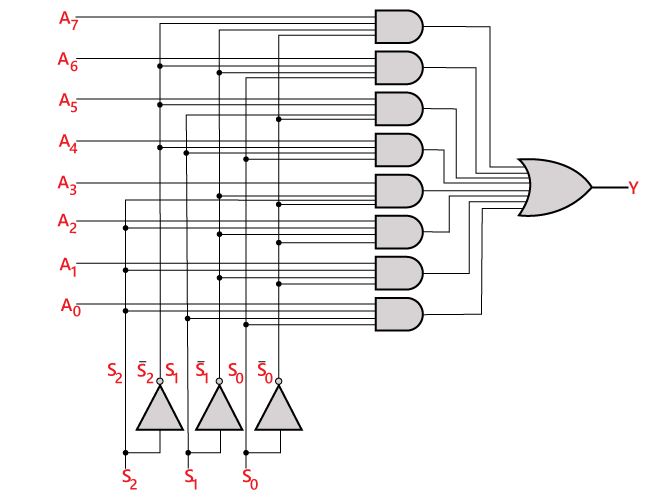
8×1 multiplexer pomocí 4×1 a 2×1 multiplexeru

Můžeme realizovat 8×1 multiplexer pomocí multiplexeru nižšího řádu. K realizaci multiplexoru 8×1 potřebujeme dva multiplexory 4×1 a jeden multiplexor 2×1. Multiplexor 4×1 má 2 selekční linky, 4 vstupy a 1 výstup. Multiplexor 2×1 má pouze 1 selekční řádek.

Pro získání 8 datových vstupů potřebujeme dva multiplexory 4×1. Multiplexor 2×1 má pouze 1 selekční řádek. Multiplexor 4×1 vytváří jeden výstup. Abychom tedy získali konečný výstup, potřebujeme 2×1 multiplexor. Blokové schéma 8×1 multiplexoru s použitím 4×1 a 2×1 multiplexoru je uvedeno níže.

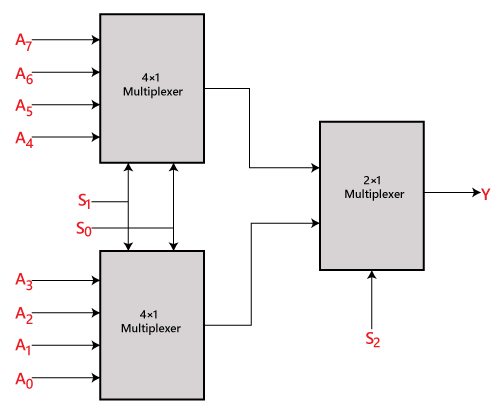
16 až 1 multiplexor

V 16 až 1 multiplexoru je celkem 16 vstupů, tj. A0, A1, …, A16, 4 selekční linky, tj, S0, S1, S2 a S3 a jeden výstup, tj. Y. Na základě kombinace vstupů, které jsou přítomny na selekčních linkách S0, S1 a S2, bude jeden z těchto 16 vstupů připojen na výstup. Blokové schéma a pravdivostní tabulka 16×1

Blokové schéma:

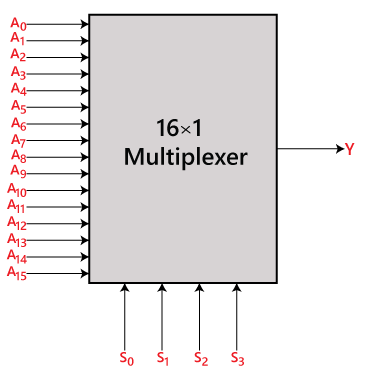
Pravdivostní tabulka:

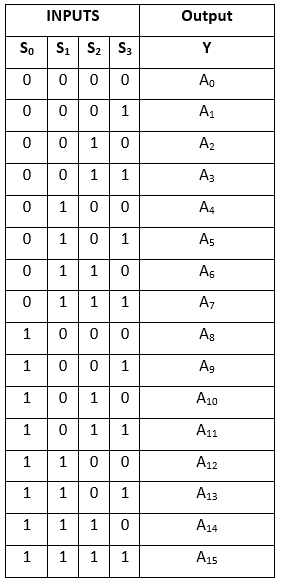
Logické vyjádření výrazu Y je následující:

Logické zapojení výše uvedeného výrazu je uvedeno níže:

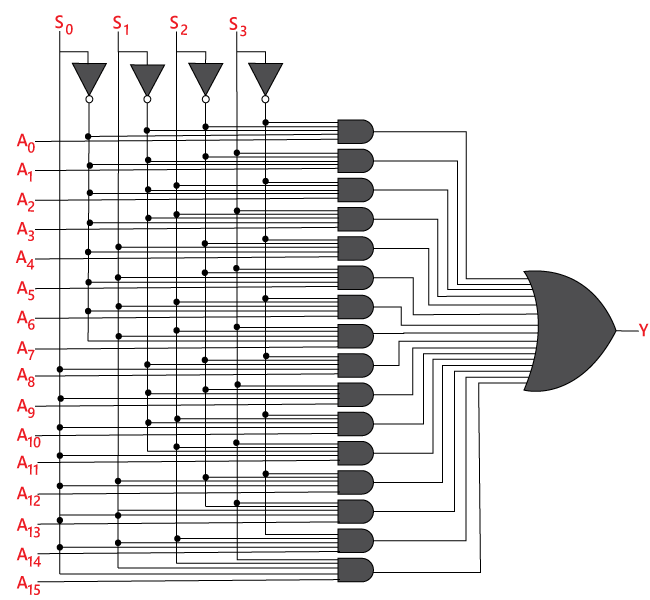
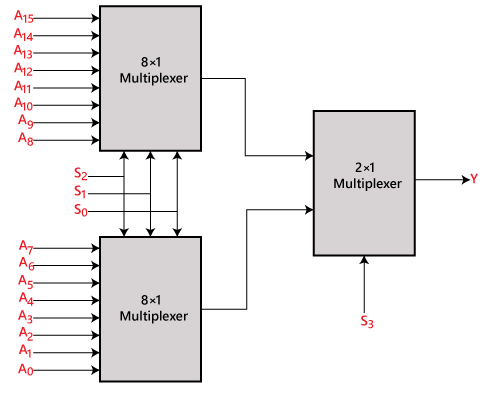
16×1 multiplexor pomocí 8×1 a 2×1 multiplexoru

Můžeme realizovat 16×1 multiplexor pomocí multiplexoru nižšího řádu. K realizaci 8×1 multiplexeru potřebujeme dva 8×1 multiplexery a jeden 2×1 multiplexer. Multiplexor 8×1 má 3 selekční linky, 4 vstupy a 1 výstup. Multiplexor 2×1 má pouze 1 selekční řádek.

Pro získání 16 datových vstupů potřebujeme dva multiplexory 8×1. V tomto případě se jedná o dva multiplexory. Multiplexor 8×1 vytváří jeden výstup. Abychom tedy získali konečný výstup, potřebujeme 2×1 multiplexor. Blokové schéma 16×1 multiplexoru s použitím 8×1 a 2×1 multiplexoru je uvedeno níže.