První graf výše ukazuje, že větší dávky skutečně urazí za epochu menší vzdálenost. Vzdálenost epochy trénování dávky 32 se pohybuje v rozmezí 0,15-0,4, zatímco u trénování dávky 256 je to přibližně 0,02-0,04. To znamená, že vzdálenost epochy trénování se pohybuje v rozmezí 0,15-0,4. Ve skutečnosti, jak vidíme na druhém grafu, se poměr vzdáleností epoch s časem zvyšuje!“
Proč ale trénování velkých dávek překonává menší vzdálenost za epochu? Je to proto, že máme méně dávek, a tedy méně aktualizací na epochu? Nebo je to proto, že každá dávková aktualizace překoná menší vzdálenost? Nebo je odpovědí kombinace obojího?“
Pro zodpovězení této otázky změřme velikost každé dávkové aktualizace.

Median batch update norm for batch size 32: 3.3e-3
Median batch update norm for batch size 256: 1.5e-3
Vidíme, že každá dávková aktualizace je menší, když je velikost dávky větší. Proč by tomu tak mělo být?
Abychom toto chování pochopili, vytvořme fiktivní scénář, kde máme dva gradientní vektory a a b, z nichž každý představuje gradient pro jeden trénovací příklad. Zamysleme se nad tím, jak se průměrná velikost aktualizace dávky pro velikost dávky=1 srovnává s velikostí dávky=2.

Použijeme-li dávku o velikosti jedna, uděláme krok ve směru a, pak b a skončíme v bodě reprezentovaném a+b. (Technicky by se gradient pro b přepočítal po aplikaci a, ale to zatím ignorujme). Výsledkem je průměrná velikost dávkové aktualizace (|a|+|b|)/2 – součet velikostí dávkových aktualizací dělený počtem dávkových aktualizací.
Použijeme-li však velikost dávky dvě, je dávková aktualizace místo toho reprezentována vektorem (a+b)/2 – červená šipka na obrázku 12. Průměrná velikost aktualizace dávky je tedy |(a+b)/2| / 1 = |a+b|/2.
Nyní porovnejme obě průměrné velikosti aktualizace dávky:

V posledním řádku jsme pomocí trojúhelníkové nerovnosti ukázali, že průměrná velikost aktualizace dávky pro velikost dávky 1 je vždy větší nebo rovna velikosti dávky 2.
Jinak řečeno, aby se průměrná velikost dávky pro velikost dávky 1 a velikost dávky 2 rovnala, musí vektory a a b směřovat stejným směrem, protože tehdy platí |a| + |b| = |a+b|. Tento argument můžeme rozšířit na n vektorů – pouze pokud všech n vektorů směřuje stejným směrem, jsou průměrné velikosti aktualizace dávky pro velikost dávky=1 a velikost dávky=n stejné. To však téměř nikdy neplatí, protože je nepravděpodobné, že by gradientní vektory směřovaly přesně stejným směrem.

Pokud se vrátíme k rovnici aktualizace minidávky na obrázku 16, v jistém smyslu říkáme, že s rostoucí velikostí dávky |B_k| se velikost součtu gradientů škáluje relativně méně rychle. To je způsobeno tím, že gradientní vektory směřují do různých směrů, a proto zdvojnásobení velikosti dávky (tj. počtu gradientních vektorů, které se mají sečíst) nezdvojnásobí velikost výsledného součtu gradientních vektorů. Zároveň dělíme jmenovatelem |B_k|, který je dvakrát větší, což vede k celkově menšímu kroku aktualizace.
Tím lze vysvětlit, proč aktualizace dávky při větších velikostech dávky bývají menší – součet gradientních vektorů se zvětší, ale nemůže plně vyrovnat větší jmenovatel|B_k|.
Hypotéza 2: Trénink s malou dávkou najde plošší minimalizátory
Nyní změříme ostrost obou minimalizátorů a vyhodnotíme tvrzení, že trénink s malou dávkou najde plošší minimalizátory. (Všimněte si, že tato druhá hypotéza může existovat současně s první – vzájemně se nevylučují). Za tímto účelem si vypůjčíme dvě metody od Keskar et al.
V první z nich vykreslíme tréninkovou a validační ztrátu podél přímky mezi minimalizátorem malé dávky (velikost dávky 32) a minimalizátorem velké dávky (velikost dávky 256). Tato přímka je popsána následující rovnicí:

kde x_l* je minimalizátor velké dávky a x_s* je minimalizátor malé dávky a alfa je koeficient mezi -1 a 2.

Jak vidíme na grafu, minimalizátor malé dávky (alfa=0) je mnohem plošší než minimalizátor velké dávky (alfa=1), který se mění mnohem ostřeji.
Poznamenejme, že se jedná o poněkud zjednodušený způsob měření ostrosti, protože zohledňuje pouze jeden směr. Keskar a spol. proto navrhují metriku ostrosti, která měří, jak moc se ztrátová funkce mění v okolí minimizátoru. Nejprve definujeme okolí takto:

kde epsilon je parametr definující velikost okolí a x je minimalizátor (váhy).
Poté definujeme metriku ostrosti jako maximální ztrátu v tomto okolí kolem minimizátoru:

kde f je ztrátová funkce, přičemž vstupy jsou váhy.
Pomocí výše uvedených definic vypočítáme ostrost minimalizačních parametrů při různých velikostech dávek s hodnotou epsilon 1e-3:
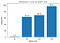
Z toho vyplývá, že minimalizátory s velkou dávkou jsou skutečně ostřejší, jak jsme viděli v interpolačním grafu.
Nakonec zkusme vykreslit minimalizátory pomocí vizualizace ztráty normalizované filtrem, jak ji formulovali Li et al . Tento typ grafu vybere dva náhodné směry se stejnými rozměry jako modelové váhy a poté normalizuje každý konvoluční filtr (nebo neuron, v případě FC vrstev) tak, aby měl stejnou normu jako odpovídající filtr v modelových vahách. Tím je zajištěno, že ostrost minimalizace není ovlivněna velikostí jejích vah. Poté vykreslí ztrátu podél těchto dvou směrů, přičemž středem grafu je minimalizátor, který chceme charakterizovat.
.