ORDRE STATA
Markov-switching modeller
Highlights
- Markov-overgangsmodellering
- Autoregressiv model
- Dynamisk regressionsmodel
- Statsafhængige regressionsparametre
- Stats-afhængige variansparametre
- Tabeller med
- Overgangssandsynligheder
- Forventede tilstandsvarigheder
- Forudsigelser
- Forventede værdier af den afhængige variabel
- Sandsynligheder for at være i en tilstand
- Statisk (én-step)
- Dynamisk (multistep)
- RMSE for forudsigelser
Hvad drejer det sig om?
Nogle gange udvikler processer sig over tid med diskrete ændringer i resultaterne.
Tænk på økonomiske recessioner og ekspansioner. I begyndelsen af en recession falder produktionen og beskæftigelsen og forbliver lav, og senere stiger produktionen og beskæftigelsen igen. Tænk på bipolære lidelser, hvor der er maniske perioder efterfulgt af depressive perioder, og hvor processen gentager sig. Statistisk set ændrer middelværdier, varianser og andre parametre sig på tværs af episoder (regimer). Vores problem er at estimere, hvornår regimerne skifter og værdierne af de parametre, der er forbundet med hvert regime. At spørge, hvornår regimer skifter, svarer til at spørge, hvor længe regimer varer ved.
I Markov-overgangsmodeller estimerer vi i tillæg til at estimere middelværdierne, varianserne osv. for hvert regime også sandsynligheden for regimeskift. De estimerede overgangssandsynligheder for et problem kan være, følgende:
| fra/til | |||||
| tilstand | 1 2 | ||||
| 1 | 0.82 0.18 | ||||
| 2 | 0.75 0.25 | ||||
Start i tilstand 1. Sandsynligheden for at overgå fra tilstand 1 til tilstand 1 er 0,82. Sagt på en anden måde: Når processen først er i tilstand 1, har den en tendens til at blive der. Med en sandsynlighed på 0,18 overgår processen imidlertid til tilstand 2. Tilstand 2 er ikke så vedholdende. Med en sandsynlighed på 0,75 vender processerne tilbage fra tilstand 2 til tilstand 1 i den næste tidsperiode.
Markov-switching-modeller er ikke begrænset til to regimer, selv om modeller med to regimer er almindelige.
I eksemplet ovenfor beskrev vi skiftet som værende pludseligt; sandsynligheden ændrede sig øjeblikkeligt. Sådanne Markov-modeller kaldes dynamiske modeller. Markov-modeller kan også rumme mere jævne ændringer ved at modellere overgangssandsynlighederne som en autoregressiv proces.
Skiftet kan således være jævnt eller pludseligt.
Lad os se, hvordan det fungerer
Lad os se på gennemsnitsændringer på tværs af regimer. Vi vil især analysere Federal Funds Rate. Federal Funds Rate er den rentesats, som USA’s centralbank opkræver af forretningsbanker for dag-til-dag-lån. Vi vil se på ændringer i Federal Funds Rate fra 1954 til udgangen af 2010. Her er dataene:
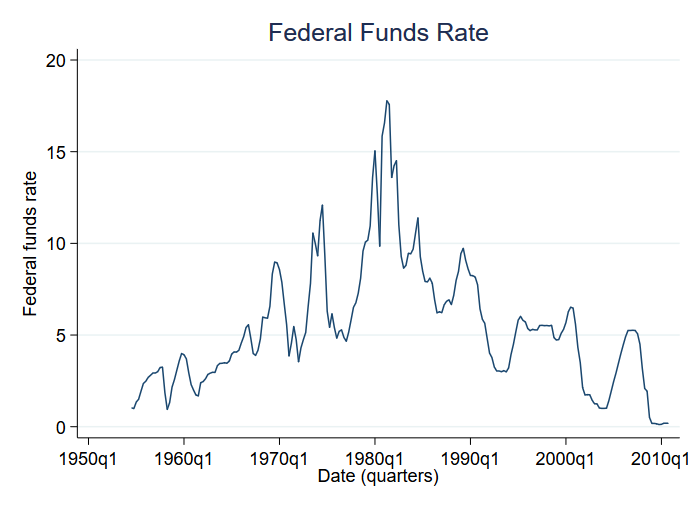
Vi har kvartalsvise data. Høje renter synes at kendetegne 70’erne og 80’erne. Vi vil antage, at der er et andet regime for lavere renter, som synes at karakterisere de andre årtier.
For at tilpasse en dynamisk-skiftende (abrupt-ændring) model med to regimer skriver vi
. mswitch dr fedfundsPerforming EM optimizaton:Performing gradient-based optimization:
| Iteration 0: | log likelihood = -508.66031 | |
| Iteration 1: | log likelihood = -508.6382 | |
| Iteration 2: | log likelihood = -508.63592 | |
| Iteration 3: | log sandsynlighed = -508.63592 | |
Markov-switching dynamisk regressionStikprøve: 1954q3 – 2010q4 Nr. of obs = 226Antal stater = 2 AIC = 4,5455Ubetingede sandsynligheder: overgang HQIC = 4,5760 SBIC = 4,6211Log likelihood = -508.63592
| fedfunds | Coef. Std. Err. z P>|z| | ||||
| State1 | |||||
| _cons | 3.70877 .1767083 20.99 0.000 3.362428 4.055112 | ||||
| State2 | |||||
| _cons | 9.556793 .2999889 31.86 0.000 8.968826 10.14476 | ||||
| sigma | 2.107562 .1008692 1.918851 2.314831 | ||||
| p11 | .9820939 .0104002 .9450805 .9943119 | ||||
| p21 | .0503587 .0268434 .0173432 .1374344 | ||||
I ovenstående output rapporteres
- middelværdierne for de to tilstande (_cons);
- en enkelt standardafvigelse for hele processen (sigma); og
- overgangssandsynlighederne for tilstand 1 til 1 og tilstand 2 til 1 (p11 og p21).
Tilstand1 er tilstanden med moderat hastighed (middelværdi på 3,71%).
Tilstand2 er tilstanden med høj sats (middelværdi 9,56 %).
| fra/til | |||||
| stat | 1 2 | ||||
| 1 | 0.98 1 – 0,98 | ||||
| 2 | 0,05 1 – 0,05 | ||||
Begge tilstande er utroligt vedholdende (1->1 og 2->2 sandsynligheder på 0,98 og 0,95).
Blandt de ting, man kan forudsige efter estimering, er sandsynligheden for at befinde sig i de forskellige tilstande. Vi har kun to tilstande, og derfor fortæller sandsynligheden for at være i (lad os sige) tilstand 2 os sandsynligheden for begge tilstande. Vi kan få den forudsagte sandsynlighed og opstille en graf over den sammen med de oprindelige data:
. predict prfed, pr
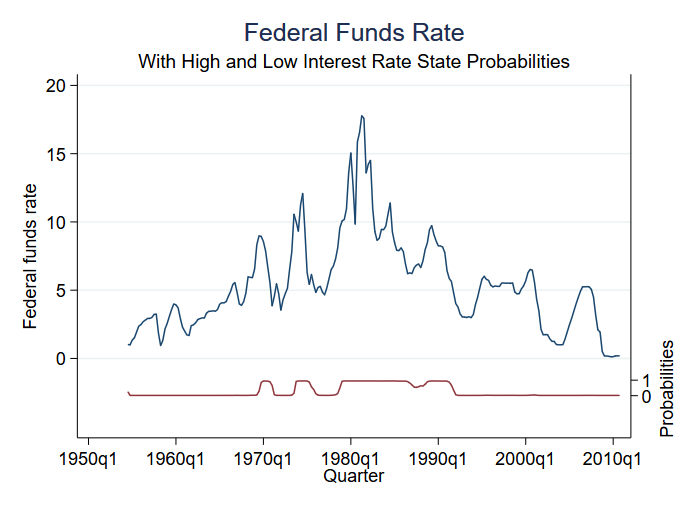
Modellen har en lille usikkerhed med hensyn til regimet på hvert tidspunkt. Vi ser tre perioder med højhastighedstilstande og fire perioder med moderathastighedstilstande.
Lad os se, hvordan det virker
Lad os se på et eksempel på et sygdomsudbrud, nemlig fåresyge pr. 10.000 indbyggere i New York City mellem 1929 og 1972. Man kunne tro, at udbrud svarer til ændringer i middelværdien, men hvad vi ser i dataene er en endnu større ændring i variansen:
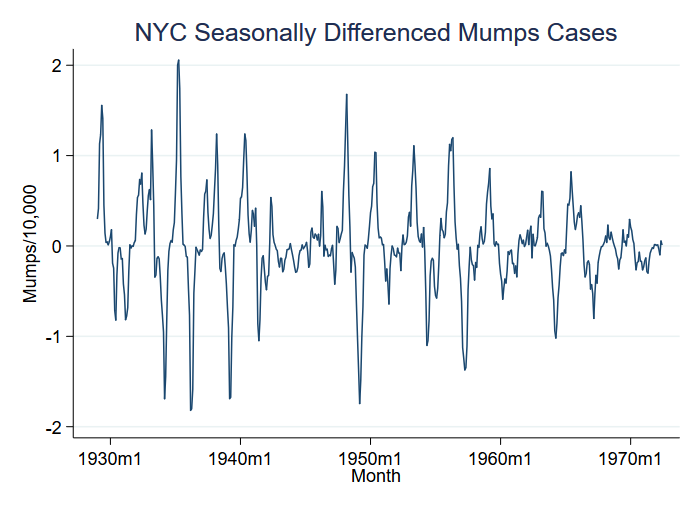
Vi har grafisk vist variablen S12.mumpspc, dvs. sæsonbestemt differentierede tilfælde af fåresyge pr. indbygger over en 12-måneders periode, og vi vil analysere S12.mumpspc.
Vi vil antage to regimer, hvor middelværdien og variansen af S12.mumpspc ændrer sig. For at tilpasse en dynamisk model (med pludselig ændring) skriver vi
. mswitch dr S12.mumpspc, varswitch switch(LS12.mumpspc, noconstant)Performing EM optimizaton:Performing gradient-based optimization:
| Iteration 0: | log sandsynlighed = 110,9372 (ikke konkav) | |
| Iteration 1: | log sandsynlighed = 120.68028 | |
| Iteration 2: | log sandsynlighed = 123.23244 | |
| Iteration 3: | log sandsynlighed = 131.47084 | |
| Iteration 3: | log sandsynlighed = 131.72182 | |
| Iteration 3: | log sandsynlighed = 131.7225 | |
| Iteration 3: | log sandsynlighed = 131.7225 | |
Markov-switching dynamisk regressionStikprøve: 1929m2 – 1972m6 Nr. obs = 521Antal tilstande = 2 AIC = -0.4826Ubetingede sandsynligheder: overgang HQIC = -0.4634 SBIC = -0.4336Log likelihood = 131.7225
| S12.mumspc | Coef. Std. Err. z P>|z| | |||
| State1 | ||||
| mumpspc | ||||
| LS12. | .4202751 .0167461 25.10 0.000 .3874533 .4530968 | |||
| State2 | ||||
| mumpspc | ||||
| LS12. | .9847369 .0258383 38.11 0.000 .9340947 1.035379 | |||
| sigma1 | .0562405 .0050954 .0470901 .067169 | |||
| sigma2 | .2611362 .0111191 .2402278 .2838644 | |||
| p11 | .762733 .0362619 .6846007 .8264175 | |||
| p12 | .1473767 .0257599 .1036675 .205294 | |||
Rapporteret er
- middelværdierne for de to tilstande i S12.mumpspc (0,42 og 0,98);
- standardafvigelserne for de to tilstande (0,06 og 0,26); og
- overgangssandsynlighederne for tilstand 1 til 1 og tilstand 2 til 1 (0,76 og 0,15).
Tilstand 1 er den tilstand med lav varians.
Det fuldstændige sæt af overgangssandsynligheder er følgende: