Dataanalyse¶
Givet et datasæt kan man bruge fit-metoden til at estimere en whitening-transformation.
fit(Whitening, X; …)¶
Skønne en whitening-transformation ud fra de data, der er givet i X. Her skal X være en matrix, hvis kolonner angiver prøverne.
Denne funktion returnerer en instans af Whitening.
Nøgleord Argumenter:
| navn | beskrivelse | default |
|---|---|---|
| regcoef |
Regulariseringskoefficienten. Kovariansen reguleres på følgende måde, når
|
zero(T) |
| mean |
Middelvektoren, som kan være en af følgende:
|
nothing |
Bemærkning: Denne funktion er internt afhængig af cov_whiten for at udlede transformationen W. Selve funktionen cov_whiten er også en nyttig funktion.
cov_whitening(C)¶
Derive the whitening transform koefficient matrix W givet covarians matrix C. Her kan C enten være en kvadratisk matrix eller en forekomst af Cholesky.
Internt er denne funktion en løsning af whitening-transformationen ved hjælp af Cholesky-faktorisering. Begrundelsen er som følger: Lad \mathbf{C} = \mathbf{U}^T \mathbf{U} og 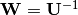 , så
, så 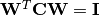 .
.
Bemærk: Returmatrixen W er en øverste trekantmatrix.
cov_whitening(C, regcoef)
Derivér en hvidtningstransformation baseret på en regulæriseret kovarians, som C + (eigmax(C) * regcoef) * eye(d).
Pakken indeholder desuden også cov_whiten!, hvor indgangsmatrixen C overskrives under beregningen. Dette kan være mere effektivt, når C ikke længere bruges.
invsqrtm(C)¶
Beregne inv(sqrtm(C)) gennem symmetrisk egenværdi-dekomposition.