Det første plot ovenfor viser, at de større batchstørrelser faktisk tilbagelægger mindre afstand pr. epoch. Afstanden for batch 32-træningsepoke varierer fra 0,15 til 0,4, mens den for batch 256-træning er omkring 0,02-0,04. Som vi kan se i det andet plot, stiger forholdet mellem epokens afstande faktisk over tid!
Men hvorfor tilbagelægger store batches mindre afstand pr. epok? Er det fordi vi har færre batches og dermed færre opdateringer pr. epoch? Eller er det, fordi hver batchopdatering tilbagelægger mindre afstand? Eller er svaret en kombination af begge dele?
For at besvare dette spørgsmål skal vi måle størrelsen af hver batchopdatering.

Median batch update norm for batch size 32: 3.3e-3
Median batch update norm for batch size 256: 1.5e-3
Vi kan se, at hver batchopdatering er mindre, når batchstørrelsen er større. Hvorfor skulle dette være tilfældet?
For at forstå denne adfærd skal vi opstille et dummy-scenarie, hvor vi har to gradientvektorer a og b, der hver repræsenterer gradienten for ét træningseksempel. Lad os tænke på, hvordan den gennemsnitlige batchopdateringsstørrelse for batchstørrelse=1 er sammenlignet med batchstørrelse=2.

Hvis vi bruger en batchstørrelse på én, tager vi et skridt i retning af a, derefter b, og ender ved det punkt, der er repræsenteret af a+b. (Teknisk set ville gradienten for b blive genberegnet efter anvendelse af a, men lad os ignorere det for nu). Dette resulterer i en gennemsnitlig batchopdateringsstørrelse på (|a|+|b|)/2 – summen af batchopdateringsstørrelserne divideret med antallet af batchopdateringer.
Hvis vi bruger en batchstørrelse på to, bliver batchopdateringen i stedet repræsenteret af vektoren (a+b)/2 – den røde pil i figur 12. Den gennemsnitlige batchopdateringsstørrelse er således |(a+b)/2| / 1 = |a+b|/2.
Nu skal vi sammenligne de to gennemsnitlige batchopdateringsstørrelser:

I den sidste linje brugte vi trekantsuligheden til at vise, at den gennemsnitlige batchopdateringsstørrelse for batchstørrelse 1 altid er større end eller lig med den for batchstørrelse 2.
Med andre ord, for at den gennemsnitlige batchstørrelse for batchstørrelse 1 og batchstørrelse 2 er lig med hinanden, skal vektorerne a og b pege i samme retning, da det er, når |a| + |b| = |a+b|. Vi kan udvide dette argument til n vektorer – kun når alle n vektorer peger i samme retning, er den gennemsnitlige batchopdateringsstørrelse for batchstørrelse=1 og batchstørrelse=n den samme. Dette er dog næsten aldrig tilfældet, da gradientvektorerne sandsynligvis ikke peger i nøjagtig samme retning.

Hvis vi vender tilbage til minibatch-opdateringsligningen i figur 16, siger vi på en måde, at når vi opskalerer batchstørrelsen |B_k|, skalerer størrelsen af summen af gradienterne forholdsvis mindre hurtigt op. Dette skyldes, at gradientvektorerne peger i forskellige retninger, og at en fordobling af batchstørrelsen (dvs. antallet af gradientvektorer, der skal summeres) derfor ikke fordobler størrelsen af den resulterende sum af gradientvektorer. Samtidig dividerer vi med en nævner |B_k|, der er dobbelt så stor, hvilket samlet set resulterer i et mindre opdateringstrin.
Dette kunne forklare, hvorfor batchopdateringerne for større batchstørrelser har tendens til at være mindre – summen af gradientvektorer bliver større, men kan ikke fuldt ud opveje den større nævner|B_k|.
Hypotese 2: Små batch-træning finder fladere minimizers
Lad os nu måle skarpheden af begge minimizers og evaluere påstanden om, at små batch-træning finder fladere minimizers. (Bemærk, at denne anden hypotese kan eksistere sammen med den første – de udelukker ikke hinanden). For at gøre dette låner vi to metoder fra Keskar et al.
I den første plotter vi trænings- og valideringstabet langs en linje mellem en lille batch-minimizer (batchstørrelse 32) og en stor batch-minimizer (batchstørrelse 256). Denne linje beskrives ved følgende ligning:

hvor x_l* er den store batch minimizer og x_s* er den lille batch minimizer, og alpha er en koefficient mellem -1 og 2.

Som vi kan se på plottet, er den lille batch-minimizer (alpha=0) meget fladere end den store batch-minimizer (alpha=1), som varierer meget mere skarpt.
Bemærk, at dette er en ret forenklet måde at måle skarphed på, da den kun tager hensyn til én retning. Derfor foreslår Keskar et al. en skarphedsmetrik, der måler, hvor meget tabsfunktionen varierer i et nabolag omkring en minimizer. Først definerer vi nabolaget som følger:

hvor epsilon er en parameter, der definerer størrelsen af nabolaget, og x er minimeringsfaktoren (vægtene).
Derpå definerer vi skarphedsmetrikken som det maksimale tab i dette kvarter omkring minimiseren:

hvor f er tabsfunktionen, hvor indgangene er vægtene.
Med ovenstående definitioner, lad os beregne skarpheden af minimizers ved forskellige batchstørrelser, med en epsilon-værdi på 1e-3:
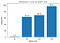
Dette viser, at de store batchminimisatorer faktisk er skarpere, som vi så i interpolationsdiagrammet.
Sidst, lad os prøve at plotte minimizers med en filternormaliseret tabsvisualisering, som formuleret af Li et al . Denne type plot vælger to tilfældige retninger med de samme dimensioner som modelvægtene og normaliserer derefter hvert konvolutionsfilter (eller neuron i tilfælde af FC-lag) til at have den samme norm som det tilsvarende filter i modelvægtene. Dette sikrer, at skarpheden af en minimizer ikke påvirkes af størrelserne af dens vægte. Derefter tegnes tabet langs disse to retninger, idet centrum af plottet er den minimizer, som vi ønsker at karakterisere.