En multiplexer er et kombinationskredsløb, der har 2n indgangsledninger og en enkelt udgangsledning. Simpelthen er multiplexeren et kombinationskredsløb med flere indgange og en enkelt udgang. Den binære information modtages fra indgangslinjerne og ledes til udgangslinjen. På grundlag af værdierne på udvælgelseslinjerne forbindes en af disse dataindgange til udgangen.
I modsætning til encoder og decoder er der n udvælgelseslinjer og 2n indgangslinjer. Der er altså i alt 2N mulige kombinationer af indgange. En multiplexer behandles også som Mux.
Der findes forskellige typer af multiplexeren, som er som følger:
2×1 Multiplexer:
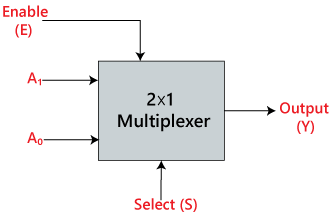
I 2×1 multiplexer er der kun to indgange, dvs, A0 og A1, 1 udvælgelseslinje, dvs. S0, og enkelte udgange, dvs. Y. På grundlag af den kombination af indgange, der er til stede på udvælgelseslinjen S0, vil en af disse 2 indgange blive forbundet til udgangen. Blokdiagrammet og sandhedstabellen for 2×1-multiplexeren er angivet nedenfor.
Blokdiagram:
Sandhedstabel:
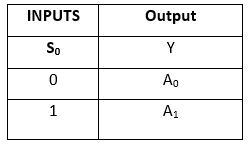
Det logiske udtryk for udtrykket Y er som følger:
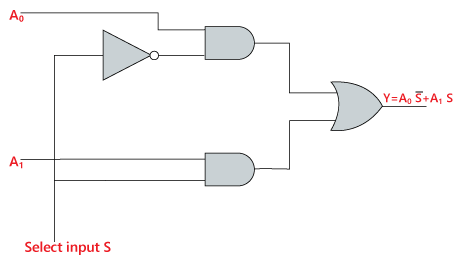
Y=S0′.A0+S0.A1
Logisk kredsløb for ovenstående udtryk er givet nedenfor:
4×1 Multiplexer:
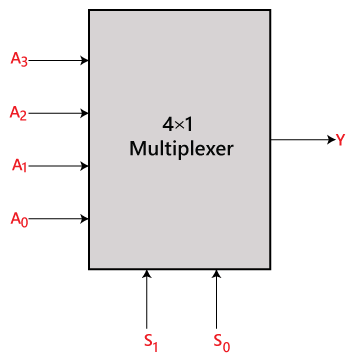
I 4×1-multiplexeren er der i alt fire indgange, dvs, A0, A1, A2 og A3, 2 valglinjer, dvs. S0 og S1, og en enkelt udgang, dvs. Y. På grundlag af den kombination af indgange, der er til stede på valglinjerne S0 og S1, forbindes en af disse 4 indgange til udgangen. Blokdiagrammet og sandhedstabellen for 4×1-multiplexeren er angivet nedenfor.
Blokdiagram:
Sandhedstabel:
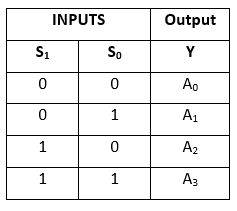
Det logiske udtryk for udtrykket Y er som følger:
Y=S1′ S0′ A0+S1′ S0 A1+S1 S0′ A2+S1 S0 A3
Det logiske kredsløb for ovenstående udtryk er givet nedenfor:
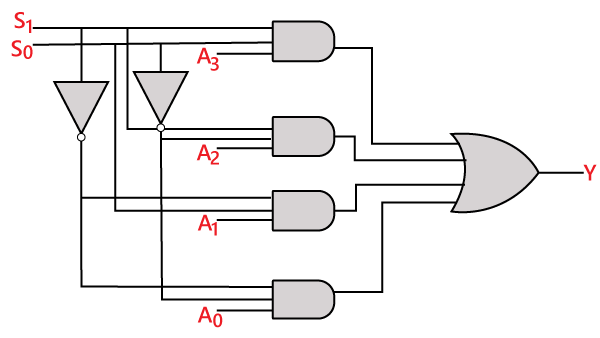
8 til 1-multiplexer
I 8 til 1-multiplexeren er der i alt otte indgange, dvs.e., A0, A1, A2, A3, A4, A5, A6 og A7, tre valglinjer, dvs. S0, S1 og S2, og en enkelt udgang, dvs. Y, på grundlag af den kombination af indgange, der er til stede på valglinjerne S0, S1 og S2, forbindes en af disse otte indgange med udgangen. Blokdiagrammet og sandhedstabellen for 8×1-multiplexeren er angivet nedenfor.
Blokdiagram:

Sandhedstabel:
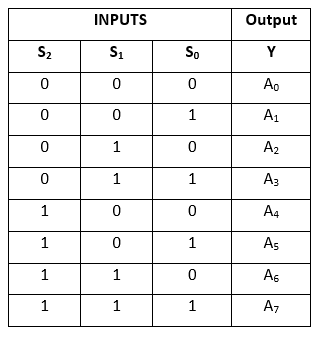
Det logiske udtryk for udtrykket Y er som følger:
Y=S0′.S1′.S1′.S2′.A0+S0.S1′.S2′.A1+S0′.S1.S2′.A2+S0.S1.S2′.A2+S0.S1.S2′.A3+S0′.S1′.S2 A4+S0.S1′.S2 A5+S0′.S1.S2 .A6+S0.S1.S3.A7
Logisk kredsløb for ovenstående udtryk er givet nedenfor:
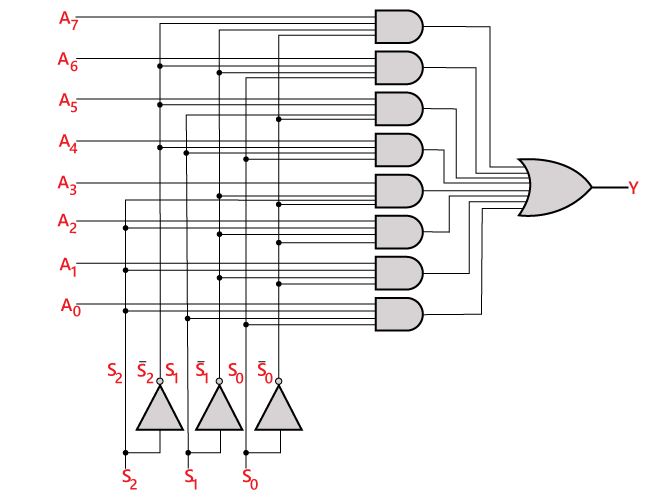
8 ×1 multiplexer ved hjælp af 4×1 og 2×1 multiplexer
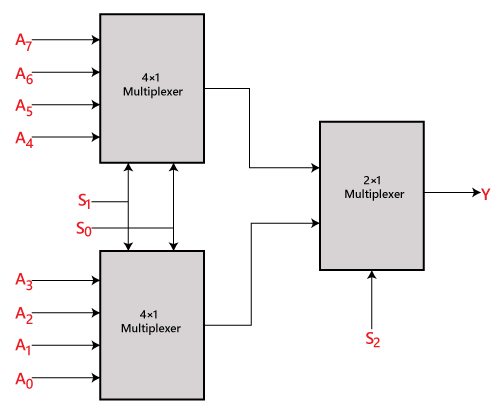
Vi kan implementere 8×1 multiplexeren ved hjælp af en multiplexer af lavere orden. For at implementere 8×1-multiplexeren har vi brug for to 4×1-multiplexere og en 2×1-multiplexer. 4×1-multiplexeren har 2 valglinjer, 4 indgange og 1 udgang. 2×1-multiplexeren har kun 1 udvælgelseslinje.
For at få 8 dataindgange har vi brug for to 4×1-multiplexere. 4×1-multiplexeren giver én udgang. Så for at få det endelige output har vi brug for en 2×1 multiplexer. Blokdiagrammet for 8×1 multiplexer ved hjælp af 4×1- og 2×1-multiplexer er vist nedenfor.
16 til 1-multiplexer
I 16 til 1-multiplexeren er der i alt 16 indgange, dvs. A0, A1, …, A16, 4 valglinjer, dvs, S0, S1, S2 og S3 og en enkelt udgang, dvs. Y. På grundlag af kombinationen af de indgange, der er til stede på valglinjerne S0, S1 og S2, vil en af disse 16 indgange blive forbundet med udgangen. Blokdiagrammet og sandhedstabellen for 16×1
Blokdiagram:
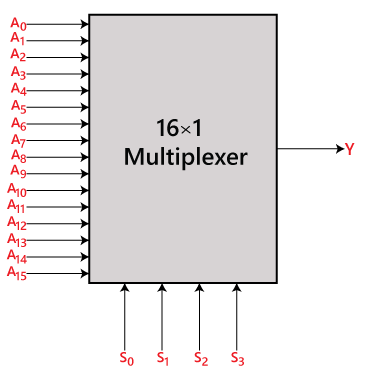
Sandhedstabellen:
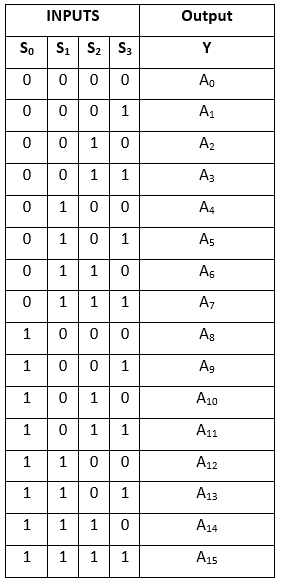
Det logiske udtryk for udtrykket Y er som følger:
Det logiske kredsløb for ovenstående udtryk er givet nedenfor:
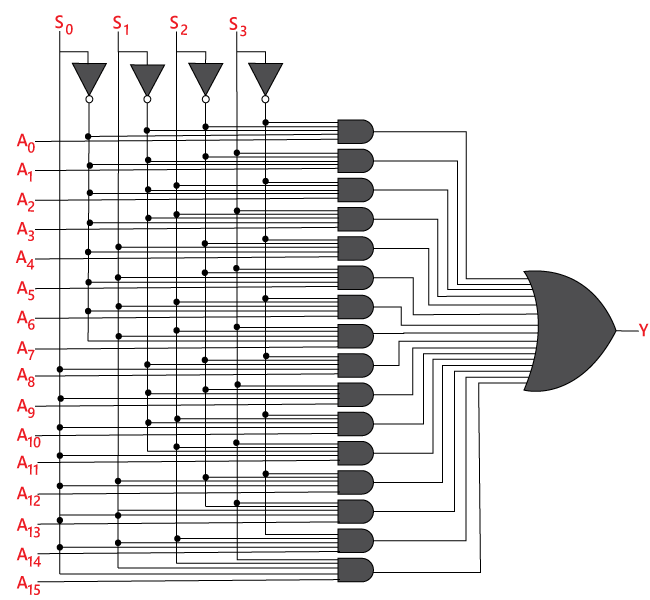
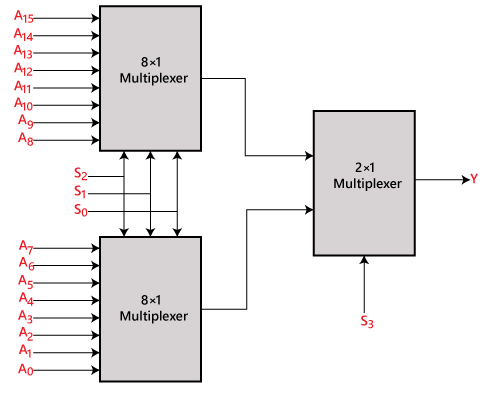
16×1 multiplexer ved hjælp af 8×1 og 2×1 multiplexer
Vi kan implementere 16×1 multiplexeren ved hjælp af en multiplexer af lavere orden. For at implementere 8×1-multiplexeren har vi brug for to 8×1-multiplexere og en 2×1-multiplexer. 8×1-multiplexeren har 3 valglinjer, 4 indgange og 1 udgang. 2×1-multiplexeren har kun 1 udvælgelseslinje.
For at få 16 dataindgange har vi brug for to 8×1-multiplexere. 8×1-multiplexeren giver én udgang. Så for at få det endelige output har vi brug for en 2×1 multiplexer. Blokdiagrammet for 16×1 multiplexer ved hjælp af 8×1 og 2×1 multiplexer er vist nedenfor.