Vergleich von PATRICIA Trie, mit seinen Nuts und Bolts, mit Hash Map

In den Mikrokosmen, in die ich eingebettet bin, ist die Datenstruktur Trie nicht sehr beliebt. Diese Umgebung besteht hauptsächlich aus Datenwissenschaftlern und, in geringerer Zahl, aus Softwareingenieuren, die mit Natural Language Processing (NLP) arbeiten.

Kürzlich fand ich mich in einer interessanten Diskussion darüber wieder, wann man Trie oder Hash-Tabelle verwenden sollte. Obwohl es in dieser Diskussion nichts Neues gab, über das ich hier berichten könnte, wie z.B. die Vor- und Nachteile dieser beiden Datenstrukturen (wenn man ein wenig googelt, findet man viele Links, die sich damit befassen), war mir neu, dass es einen speziellen Typ von Trie gibt, der Patricia Trie genannt wird, und dass diese Datenstruktur in einigen Szenarien sowohl in der Verarbeitungszeit als auch im Platzbedarf vergleichbar mit einer Hashtabelle ist, während sie Aufgaben wie die Auflistung von Zeichenketten mit gemeinsamem Präfix ohne zusätzliche Kosten bewältigt.

Mit diesem Gedanken im Hinterkopf suchte ich nach einer Geschichte oder einem Blog, um auf einfache Weise (Euphemismus für Faulheit) zu verstehen, wie der PATRICIA-Algorithmus funktioniert, insbesondere als Abkürzung zur Lektüre des 1968 veröffentlichten 21 Seiten langen Papiers. Leider war ich bei dieser Suche nicht erfolgreich, so dass mir keine Alternative zur Lektüre blieb.

Mit dieser Geschichte möchte ich die oben genannte Lücke füllen, d.h. eine Geschichte schreiben, die den vorliegenden Algorithmus in laienhaften Worten beschreibt.

Um mein Ziel zu erreichen, werde ich zunächst, für diejenigen, die mit Versuchen nicht vertraut sind, diese Datenstruktur kurz vorstellen. Nach dieser Einführung werde ich die populärsten Trie auflisten, die es gibt, um dann im Detail zu beschreiben, wie PATRICIA Trie funktioniert und warum sie so gut funktionieren. Zum Schluss werde ich die Ergebnisse (Leistung und Speicherplatzverbrauch) in zwei verschiedenen Anwendungen vergleichen: die erste ist eine Wortzählung (<WORT, FREQUENZ>-Tupel) auf der Grundlage eines ziemlich großen Textes; die zweite ist der Aufbau eines <URL, IP>-Tupels auf der Grundlage einer Liste von mehr als 2 Millionen URLs, die aus dem Kernelement eines DNS-Servers besteht. Beide Anwendungen wurden auf der Grundlage von Hash Map und Patricia Trie erstellt.

Nach der Definition von Sedgewick und Wayne von der Princeton University in ihrem Buch Algorithms – Fourth Edition (Verlag: Addison-Wesley) ist ein Trie oder Präfixbaum „eine Datenstruktur, die aus den Zeichen des Suchschlüssels aufgebaut ist, um die Suche zu leiten“. Diese „Datenstruktur besteht aus Knoten, die Verknüpfungen enthalten, die entweder Null sind oder auf andere Knoten verweisen. Auf jeden Knoten verweist nur ein anderer Knoten, der als sein Elternteil bezeichnet wird (mit Ausnahme eines Knotens, der Wurzel, auf die kein Knoten verweist), und jeder Knoten hat S Verknüpfungen, wobei S der Umfang des Alphabets (oder Zeichensatzes) ist“.

Abbildung 1 unten enthält, der obigen Definition folgend, ein Beispiel für einen Trie.

Der Wurzelknoten hat keine Bezeichnung. Er hat drei Kinder: Knoten mit dem Schlüssel ‚a‘, ‚h‘ und ’s‘. In der unteren rechten Ecke der Abbildung befindet sich eine Tabelle, in der alle Schlüssel mit ihrem jeweiligen Wert aufgeführt sind. Von der Wurzel können wir zu ‚a‘ -> ‚i‘ -> ‚r‘ traversieren. Diese Abfolge bildet das Wort „air“ mit einem Wert (z. B. die Anzahl der Vorkommen dieses Wortes in einem Text) von 4 (die Werte befinden sich in einem grünen Kasten). Vereinbarungsgemäß hat ein vorhandenes Wort in einer Symboltabelle einen Wert, der nicht Null ist. Das Wort „airway“ existiert zwar im Englischen, ist aber nicht in dieser Tabelle enthalten, weil der Wert des Knotens mit dem Schlüssel ‚y‘ gemäß der Konvention null ist.

Das Wort „air“ ist auch die Vorsilbe für die Wörter: „airplane“; und „airways“. Die Sequenz ‚h‘ -> ‚a‘ bildet das Präfix von „hat“ und „Hut“, so wie die Sequenz ‚h‘ -> ‚o‘ das Präfix von „Haus“ und „Pferd“ bildet.

Neben der Funktion als Datenstruktur für, sagen wir, ein Wörterbuch, dient es auch als wichtiges Element einer Vervollständigungsanwendung. Ein System könnte die Wörter „airplane“ und „airways“ vorschlagen, nachdem ein Benutzer das Wort „air“ eingetippt hat, indem es den Teilbaum durchläuft, dessen Wurzel der Knoten mit dem Schlüssel „r“ ist. Ein zusätzlicher Vorteil dieser Struktur ist, dass man ohne zusätzliche Kosten eine geordnete Liste der vorhandenen Schlüssel erhalten kann, indem man den Trie in einer geordneten Orientierung durchläuft, die Kinder eines Knotens stapelt und sie von links nach rechts durchläuft.

In Abbildung 2 ist die Anatomie des Knotens beispielhaft dargestellt.

Das Interessante an dieser Anatomie ist, dass die Zeiger der Kinder normalerweise in einem Array gespeichert werden. Wenn wir einen Zeichensatz S, z. B. Extended ASCII, darstellen, muss das Array 256 Zeichen groß sein. Wenn wir ein Kind-Zeichen haben, können wir in O(1)-Zeit auf den Zeiger in seinem Elternteil zugreifen. Wenn man bedenkt, dass die Größe des Vokabulars N und die Größe des längsten Wortes M ist, ist die Tiefe des Trie ebenfalls M und es dauert O(MN), um die Struktur zu durchlaufen. Wenn wir bedenken, dass N normalerweise viel größer als M ist (die Anzahl der Wörter in einem Korpus ist viel größer als die Größe des längsten Wortes), können wir O(MN) als linear betrachten. In der Praxis ist dieses Array spärlich, d.h. die meisten Knoten haben viel weniger Kinder als S. Außerdem ist die durchschnittliche Größe der Wörter kleiner als M, so dass es in der Praxis im Durchschnitt O(logₛ N) dauert, nach einem Schlüssel zu suchen, und O(N logₛ N), die gesamte Struktur zu durchlaufen.

Es gibt zwei Hauptprobleme mit dieser Datenstruktur. Das eine ist der Platzbedarf. Auf jeder Ebene L, beginnend mit Null, gibt es gleich viele Sᴸ Zeiger. Während dies bei Extended ASCII, d.h. 256 Zeichen, ein Problem bei begrenztem Speicher darstellt, verschlechtert sich die Situation, wenn man alle Unicode-Zeichen (65.000) berücksichtigt. Das zweite Problem ist die Anzahl der Knoten mit nur einem Kind, was die Eingabe- und Suchleistung verschlechtert. In dem Beispiel in Abbildung 1 haben nur die Wurzel, der Schlüssel „h“ auf Ebene 1, die Schlüssel „a“ und „o“ auf Ebene 2 und der Schlüssel „r“ auf Ebene 3 mehr als ein Kind. Mit anderen Worten: Nur 5 der 27 Knoten haben zwei oder mehr Kinder. Die Alternativen zu dieser Struktur befassen sich hauptsächlich mit diesen Problemen.

Bevor ich die Alternative (PATRICIA Trie) beschreibe, werde ich die folgende Frage beantworten: Warum Alternativen, wenn wir eine Hashtabelle anstelle eines Arrays verwenden können? Eine Hash-Tabelle hilft zwar, bei geringer Leistungseinbuße Speicherplatz zu sparen, löst aber das Problem nicht. Je höher man sich im Trie befindet (näher an Level Null), desto wahrscheinlicher ist es, dass fast alle Zeichen in jedem Zeichensatz angesprochen werden müssen. Gut implementierte Hash-Tabellen, wie die in Java (die definitiv zu den besten gehören), beginnen mit einer Standardgröße und passen die Größe automatisch an einen Schwellenwert an. In Java beträgt die Standardgröße 16 mit einem Schwellenwert von 0,75 und verdoppelt ihre Größe bei jeder dieser Operationen. Wenn die Anzahl der Kinder in einem Knoten 192 erreicht, wird die Größe der Hashtabelle bei Extended ASCII auf 512 erhöht, obwohl am Ende nur 256 benötigt werden.

Radix Trie

Da PATRICIA Trie ein Spezialfall von Radix Trie ist, beginne ich mit letzterem. In Wikipedia wird ein Radix-Trie definiert als „eine Datenstruktur, die einen raumoptimierten Trie darstellt… bei dem jeder Knoten, der das einzige Kind ist, mit seinem Elternteil verschmolzen wird… Im Gegensatz zu regulären Bäumen (bei denen ganze Schlüssel en masse von ihrem Anfang bis zum Punkt der Ungleichheit verglichen werden), wird der Schlüssel an jedem Knoten Bit für Bit verglichen, wobei die Anzahl der Bits in diesem Bit an diesem Knoten die Radix r des Radix-Tries ist“. Diese Definition macht mehr Sinn, wenn wir diesen Trie in Abbildung 3 veranschaulichen.

Die Anzahl der Kinder r eines Knotens in einem Radix-Trie wird durch die folgende Formel bestimmt, wobei x die Anzahl der Bits ist, die erforderlich ist, um den oben erwähnten Chunk-of-Bits zu vergleichen:

Die obige Formel legt fest, dass die Anzahl der Kinder in einem Radix-Trie immer ein Vielfaches von 2 ist. Zum Beispiel für ein 4-Radix Trie, x = 2. Das bedeutet, dass wir Stücke von zwei Bits, ein Bitpaar, vergleichen müssen, denn mit diesen zwei Bits stellen wir alle Dezimalzahlen von 0 bis 3 dar, also insgesamt 4 verschiedene Zahlen, eine für jedes Kind.

Um die obigen Definitionen besser zu verstehen, betrachten wir das Beispiel in Abbildung 3. In diesem Beispiel haben wir einen hypothetischen Zeichensatz bestehend aus 5 Zeichen (NULL, A, B, C und D). Ich habe mich dafür entschieden, sie mit nur 4 Bits darzustellen (dies hat nichts mit r zu tun, man braucht nur 3 Bits, um 5 Zeichen darzustellen, sondern mit der Einfachheit der Darstellung des Beispiels). In der oberen linken Ecke der Abbildung befindet sich eine Tabelle, die jedes Zeichen seiner Bit-Darstellung zuordnet.

Um das Zeichen ‚A‘ einzufügen, werde ich es bitweise mit dem NULL-Zeichen vergleichen. In der oberen rechten Ecke von Abbildung 3, in dem mit 1 gekennzeichneten Kasten in einer gelben Raute, können wir sehen, dass sich diese beiden Zeichen beim ersten Paar unterscheiden. Dieses erste Paar wird in der 4-Bit-Darstellung von A in Rot dargestellt. DIFF enthält also die Bitposition, an der das unterschiedliche Paar endet.

Um das Zeichen ‚B‘ einzufügen, müssen wir es bitweise mit dem Zeichen ‚A‘ vergleichen. Dieser Vergleich findet in dem mit 2 gekennzeichneten Rautenfeld statt. Die Differenz fällt diesmal auf das zweite Bitpaar, in rot, das an Position 4 endet. Da das zweite Paar 01 ist, erstellen wir einen Knoten mit dem Schlüssel B und verweisen die Adresse 01 am Knoten A auf diesen. Diese Verknüpfung ist im unteren Teil von Abbildung 3 zu sehen. Das gleiche Verfahren gilt für das Einfügen der Zeichen ‚C‘ und ‚D‘.

Im obigen Beispiel sehen wir, dass das erste Paar (01 in blau) das Präfix aller eingefügten Zeichen ist.

Dieses Beispiel dient dazu, den in der obigen Radix-Trie-Definition erwähnten Chunk-of-Bits-Vergleich, die Platzoptimierung (in diesem Fall nur vier Kinder, unabhängig von der Größe des Zeichensatzes) und die Eltern-Kind-Fusion (in den Kinderknoten werden nur die Bits gespeichert, die sich von der Wurzel unterscheiden) zu beschreiben. Dennoch gibt es immer noch einen Link, der auf einen Nullknoten zeigt. Die Sparsamkeit ist direkt proportional zu r und der Tiefe des Tries.

PATRICIA Trie

PATRICIA (Practical Algorithm to Retrieve Information Coded in Alphanumeric, Journal of the ACM, 15(4):514-534, October 1968) . Ja, PATRICIA ist ein Akronym!

PATRICIA Trie ist hier durch drei Regeln definiert:

1. Jeder Knoten (TWIN ist der ursprüngliche Begriff von PATRICIA) hat zwei Kinder (r = 2 und x = 1 in den Begriffen des Radix-Tries);
2. Ein Knoten wird nur dann in ein Präfix (L-PHRASE in den Begriffen von PATRICIA) mit zwei Kindern aufgeteilt (jedes Kind bildet einen BRANCH, der der ursprüngliche Begriff von PATRICIA ist), wenn zwei Wörter (PROPER OCCURRENCE in den Begriffen von PATRICIA) das gleiche Präfix haben; und
3. Jedes Wort, das endet, wird mit einem Wert innerhalb des Knotens dargestellt, der von Null verschieden ist (END-Markierung in PATRICIAs ursprünglicher Nomenklatur)

Die obige Regel Nummer 2 bedeutet, dass die Länge des Präfixes auf jeder Ebene größer ist als die Länge des Präfixes der vorherigen Ebene. Dies wird in den Algorithmen, die PATRICIA-Operationen wie das Einfügen eines Elements oder die Suche nach einem anderen Element unterstützen, sehr wichtig sein.

Aus den obigen Regeln kann man den Knoten wie unten dargestellt definieren. Jeder Knoten hat einen Elternteil, außer der Wurzel, und zwei Kinder, einen Wert (beliebiger Typ) und eine Variable diff, die die Position angibt, an der sich der Split im Schlüsselbitcode befindet

Um den PATRICIA-Algorithmus zu verwenden, benötigen wir eine Funktion, die bei zwei Zeichenketten die Position des ersten Bits von links nach rechts zurückgibt, bei dem sie sich unterscheiden. Wir haben bereits gesehen, dass dies für den Radix-Trie funktioniert.

Um den Trie mit PATRICIA zu bedienen, d.h. um Schlüssel darin einzufügen oder zu finden, brauchen wir 2 Zeiger. Der eine ist parent, initialisiert durch Zeigen auf den Wurzelknoten. Der zweite ist child, initialisiert durch Zeigen auf das linke Kind der Wurzel.

Im Folgenden wird die Variable diff die Position enthalten, an der sich der eingefügte Schlüssel von child.key unterscheidet. Nach Regel Nummer 2 definieren wir die folgenden 2 Ungleichungen:

Lass found auf den Knoten zeigen, an dem die Suche nach einem Schlüssel endet. Wenn found.key sich von der eingefügten Zeichenkette unterscheidet, wird diff mit Hilfe einer ComputeDiff-Funktion aus dieser Zeichenkette und found.key berechnet. Wenn sie gleich sind, existiert der Schlüssel in der Struktur, und wie in jeder Symboltabelle sollte der Wert zurückgegeben werden. Eine Hilfsmethode namens BitAtPosition, die das Bit an einer bestimmten Position (0 oder 1) abruft, wird während der Operationen verwendet.

Für die Suche müssen wir eine Funktion Search(key) definieren. Ihr Pseudocode ist in Abbildung 4 zu sehen.

Die zweite Funktion, die wir in dieser Geschichte verwenden werden, ist Insert(key). Ihr Pseudocode ist in Abbildung 6 zu sehen.

In dem obigen Pseudocode gibt es eine Methode zum Erstellen eines Knotens namens CreateNode. Ihre Argumente können aus Abbildung 4 entnommen werden.

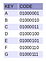
Um zu veranschaulichen, wie ein PATRICIA-Trie funktioniert, ziehe ich es vor, den Leser Schritt für Schritt anzuleiten, um das Einfügen von 7 Zeichen (‚A‘, ‚B‘, ‚C‘, ‚D‘, ‚E‘, ‚F‘ und ‚G‘, wie in nebenstehender Abbildung 7 angegeben) in ihrer natürlichen Reihenfolge abzuschließen. Am Ende wird man hoffentlich verstanden haben, wie diese Datenstruktur funktioniert.

Zeichen A ist das erste, das eingefügt wird. Sein Bitcode ist 01000001. Wie bei Radix Trie vergleichen wir diesen Bitcode mit dem an der Wurzel, der in diesem Moment Null ist, wir vergleichen also 00000000 mit 01000001. Die Differenz fällt an Position 2 (da x = 1 ist, vergleichen wir hier Bit für Bit und nicht ein Paar).

Um den Knoten zu erstellen, müssen wir das linke und rechte Kind auf ihre jeweiligen Nachfolger verweisen. Da dieser Knoten die Wurzel ist, zeigt sein linkes Kind definitionsgemäß auf sich selbst, während sein rechtes Kind auf null zeigt. Dies wird der einzige Null-Zeiger im gesamten Trie sein. Es sei daran erinnert, dass die Wurzel der einzige Knoten ist, der keine Eltern hat. Der Wert, in unserem Beispiel Ganzzahlen, die eine Wortzählungsanwendung nachahmen, wird auf 1 gesetzt. Das Ergebnis dieser Einfügeoperation ist in Abbildung 8 dargestellt.

Als nächstes fügen wir das Zeichen B mit dem Bitcode 01000010 ein. Als erstes muss geprüft werden, ob dieses Zeichen bereits in der Struktur vorhanden ist. Zu diesem Zweck suchen wir nach diesem Zeichen. Die Suche in einem PATRICIA-Trie ist einfach (siehe Pseudocode in Abbildung 5). Nach dem Vergleich des Schlüssels der Wurzel mit dem Schlüssel von B kommt man zu dem Schluss, dass sie unterschiedlich sind, so dass wir mit der Erstellung von 2 Zeigern fortfahren: parent und child. Anfänglich zeigt parent auf die Wurzel und child auf das linke Kind der Wurzel. In diesem Fall zeigen beide auf den Knoten A. Regel Nummer 2 folgend, iterieren wir die Struktur, während die Ungleichung (1) wahr ist.

In diesem Moment ist parent.DIFF gleich und nicht kleiner als child.DIFF. Dies bricht die Ungleichung (1). Da child.VALUE anders ist als null (gleich 1), vergleichen wir die Zeichen. Da A sich von B unterscheidet, bedeutet dies, dass B nicht im Trie enthalten ist und eingefügt werden muss.

Um einzufügen, beginnen wir wieder mit der Definition von parent und child wie zuvor, d.h. parent zeigt auf die Wurzel und child zeigt auf den linken Knoten. Die Iteration durch die Struktur muss den Ungleichungen (1) und (2) folgen. Wir fahren fort mit der Berechnung von diff, der bitweisen Differenz zwischen B und child.KEY, die in diesem Stadium gleich A ist (Differenz zwischen den Bitcodes 01000001 und 01000010). Die Differenz fällt auf das Bit an Position 7, also diff = 7.

Zu diesem Zeitpunkt zeigen parent und child auf denselben Knoten (auf Knoten A, die Wurzel). Da die Ungleichung (1) bereits falsch ist und child.DIFF kleiner als diff ist, werden wir den Knoten B erstellen und parent.LEFT auf ihn zeigen lassen. Wie beim Knoten A müssen wir auch die Kinder des Knotens B irgendwo hinweisen. Das Bit an Position 7 in B ist 1, also zeigt das rechte Kind des Knotens B auf sich selbst. Das linke Kind des Knotens B zeigt auf den Elternteil, in diesem Fall die Wurzel. Das Endergebnis ist in Abbildung 9 dargestellt.

Indem wir das linke Kind des Knotens B auf sein Elternteil zeigen lassen, ermöglichen wir die in Regel Nummer 2 erwähnte Aufteilung. Wenn wir ein Zeichen einfügen, dessen Diff zwischen 2 und 7 liegt, schickt uns dieser Zeiger zurück an die richtige Position, von der aus wir das neue Zeichen einfügen. Dies wird geschehen, wenn wir das Zeichen D einfügen.

Aber vorher müssen wir das Zeichen C einfügen, dessen Bitcode gleich 01000011 ist. Der Zeiger parent zeigt auf den Knoten A (die Wurzel). Anders als bei der Suche nach dem Zeichen B zeigt diesmal das Kind auf den Knoten B (damals zeigten beide Zeiger auf die Wurzel).

In diesem Moment gilt Ungleichung (1) (parent.DIFF ist kleiner als child.DIFF), also aktualisieren wir beide Zeiger, indem wir parent auf child und child auf das rechte Kind des Knotens B setzen, weil das Bit von C an Position 7 1 ist.

Nach der Aktualisierung zeigen beide Zeiger auf den Knoten B, wodurch Ungleichung (1) aufgelöst wird. Wie zuvor vergleichen wir den Bitcode von child.KEY mit dem Bitcode von C (01000010 mit 01000011) und stellen fest, dass sie sich an Position 8 unterscheiden. Da das Bit von C an Position 7 1 ist, wird dieser neue Knoten (Knoten C) das rechte Kind von B sein. An Position 8 ist das Bit von C 1, so dass wir das rechte Kind von Knoten C auf sich selbst setzen, während das linke Kind in diesem Moment auf den Elternknoten B zeigt. Der resultierende Trie ist in Abbildung 10 dargestellt.

Das nächste Zeichen ist D (Bitcode 01000100). Wie bei der Einfügung des Zeichens C setzen wir zunächst den Zeiger parent auf den Knoten A und den Zeiger child auf den Knoten B. Gleichung (1) ist gültig, also aktualisieren wir die Zeiger. Jetzt zeigt parent auf den Knoten B und child auf das linke Kind des Knotens B, denn an Position 7 ist das Bit von D 0. Anders als beim Einfügen des Zeichens C zeigt child jetzt wieder auf den Knoten A, wodurch die Ungleichung (1) aufgehoben wird. Wieder berechnen wir die Differenz zwischen den Bitcodes von A und D. Jetzt ist diff gleich 6. Wieder setzen wir parent und child, wie wir es normalerweise tun. Während die Ungleichung (1) gültig ist, gilt Ungleichung (2) nicht. Das bedeutet, dass wir D als linkes Kind von A einfügen. Aber was ist mit den Kindern von D? An Position 6 ist das Bit von D gleich 1, so dass sein rechtes Kind auf sich selbst zeigt. Das Interessante daran ist, dass das linke Kind des Knotens D nun auf den Knoten B zeigt, wodurch das in Abbildung 11 gezeichnete Trie erreicht wird.

Nächstes Zeichen ist E mit dem Bitcode 01000101. Die Suchfunktion liefert den Knoten D. Der Unterschied zwischen den Zeichen D und E fällt auf das Bit an Position 8. Da das Bit von E an Position 6 1 ist, wird es rechts von D positioniert. Die Struktur des Trie ist in Abbildung 12 dargestellt.

Das Interessante beim Einfügen des Zeichens F ist, dass sein Platz zwischen den Zeichen D und E ist, weil die Differenz zwischen D und F an Position 7 ist. An Position 7 ist das Bit von E jedoch 0, so dass der Knoten E das linke Kind des Knotens F ist. Die Struktur ist nun in Abbildung 13 dargestellt.

Und zuletzt fügen wir das Zeichen G ein. Nach allen Berechnungen kommen wir zu dem Schluss, dass der neue Knoten als rechtes Kind von Knoten F mit diff gleich 8 platziert werden sollte. Das Endergebnis ist in Abbildung 14 dargestellt.

Bis jetzt haben wir Zeichenfolgen eingefügt, die nur aus einem Zeichen bestehen. Was würde passieren, wenn wir versuchen würden, die Zeichenfolgen AB und BA einzufügen? Der interessierte Leser kann diesen Satz als Übung nehmen. Zwei Hinweise: Beide Zeichenketten unterscheiden sich vom Knoten B an der Position 9; und das endgültige Trie ist in Abbildung 15 dargestellt.

Wenn man über die letzte Abbildung nachdenkt, kann man die folgende Frage stellen: Um z.B. die Zeichenkette BA zu finden, benötigt man 5 Bit-Vergleiche, während zur Berechnung des Hash-Codes dieser Zeichenkette nur zwei Iterationen erforderlich sind. Wann wird der PATRICIA-Trie also konkurrenzfähig? Stellen Sie sich vor, wir fügen in diese Struktur die Zeichenkette ABBABABBBBABABBA (aus dem Beispiel im PATRICIA-Originalpapier von 1968) ein, die 16 Zeichen lang ist? Diese Zeichenfolge würde als linkes Kind des Knotens AB mit diff an Position 17 platziert werden. Um sie zu finden, bräuchten wir 5 Bit-Vergleiche, während die Berechnung des Hash-Codes 16 Iterationen erfordern würde, eine für jedes Zeichen. Dies ist der Grund, warum PATRICIA Trie bei der Suche nach langen Zeichenfolgen so konkurrenzfähig ist.

PATRICIA Trie vs. Hash Map

In diesem letzten Abschnitt werde ich Hash Map und PATRICIA Trie in zwei Anwendungen vergleichen. Die erste ist eine Wortzählung auf leipzig1m.txt, die 1 Million zufällige Sätze enthält, und die zweite ist das Auffüllen einer Symboltabelle mit mehr als 2,3 Millionen URLs aus dem DMOZ-Projekt (2017 geschlossen), das von hier heruntergeladen wurde.

Der Code, den ich entwickelt und verwendet habe, um sowohl den obigen Pseudocode zu implementieren als auch die Leistung von PATRICIA Trie mit Hash Table zu vergleichen, kann auf meinem GitHub gefunden werden.

Diese Vergleiche wurden auf meiner Ubuntu 18.04-Box ausgeführt. Die Konfiguration ist in Abbildung 16 zu sehen