Mikrokosmoksissa, joihin olen upotettu, trie-tietorakenne ei ole kovin suosittu. Tämä ympäristö koostuu pääasiassa datatieteilijöistä ja pienemmässä osassa ohjelmistoinsinööreistä, jotka työskentelevät luonnollisen kielenkäsittelyn (Natural Language Processing, NLP) parissa.
Löysin itseni hiljattain mielenkiintoisesta keskustelusta siitä, milloin kannattaa käyttää trie- vai hash-taulukkoa. Vaikka tuossa keskustelussa ei ollut mitään uutta, josta voisin raportoida tässä, kuten näiden kahden tietorakenteen hyvät ja huonot puolet (jos googletat hieman, löydät monia linkkejä, jotka käsittelevät niitä), minulle uutta oli erityyppinen trie nimeltään Patricia Trie ja se, että joissakin skenaarioissa tämä tietorakenne suoriutuu vertailukelpoisella tavalla sekä käsittelyajassa että tilassa hash-taulukkoon nähden, samalla kun se käsittelee sellaisia tehtäviä kuin merkkijonojen listaaminen, joilla on yhteinen etuliite ilman lisäkustannuksia.
Tässä mielessä etsin tarinaa tai blogia, joka auttaisi minua ymmärtämään yksinkertaisella tavalla (kiertoilmaus laiskuudelle), miten PATRICIA-algoritmi toimii, ja joka erityisesti toimisi oikotienä vuonna 1968 julkaistun 21 sivun mittaisen paperin lukemiseen. Valitettavasti en onnistunut tässä etsinnässä, eikä minulle jäänyt vaihtoehtoa sen lukemiselle.
Tavoitteeni tällä tarinalla on täyttää edellä mainittu aukko, eli saada tarina, joka kuvaa maallikon kielellä käsillä olevaa algoritmia.
Tavoitteeni saavuttamiseksi esittelen ensin lyhyesti, niille, jotka eivät ole perehtyneet yrittämiseen, tämän tietorakenteen. Tämän esittelyn jälkeen luettelen suosituimpia trieitä, joiden avulla voin toteuttaa ja kuvata yksityiskohtaisesti, miten PATRICIA Trie toimii ja miksi ne toimivat niin hyvin. Lopetan tämän tarinan vertailemalla tuloksia (suorituskyky ja tilankulutus) kahdessa eri sovelluksessa: ensimmäinen on sanojen laskenta (<WORD, FREQUENCY> -tuplet), joka perustuu melko suureen tekstiin; ja toinen on <URL, IP> -tuplettien rakentaminen, joka perustuu yli 2 miljoonan URL-osoitteen luetteloon, joka koostuu DNS-palvelimen ydinelementistä. Molemmat sovellukset rakennettiin Hash Mapin ja Patricia Trie:n pohjalta.
Kuten Sedgewick ja Wayne Princetonin yliopistosta määrittelevät kirjassaan Algorithms – Fourth Edition (kustantaja: Addison-Wesley) trie eli etuliitepuu on ”hakuavaimen merkeistä rakennettu tietorakenne, joka ohjaa hakua”. Tämä ”tietorakenne koostuu solmuista, jotka sisältävät linkkejä, jotka ovat joko nolla tai viittaavat muihin solmuihin. Jokaista solmua osoittaa vain yksi toinen solmu, jota kutsutaan sen vanhemmaksi (lukuun ottamatta yhtä solmua, juurta, johon ei osoiteta yhtään solmua), ja jokaisella solmulla on S linkkiä, jossa S on aakkosten koko (tai merkistö)”.
Alhaalla olevassa kuvassa 1 on edellä esitetyn määritelmän mukaisesti esimerkki triestä.

Juurisolmulla ei ole osoitetta. Sillä on kolme lasta: solmut, joiden avaimet ovat ’a’, ’h’ ja ’s’. Kuvion oikeassa alakulmassa on taulukko, jossa luetellaan kaikki avaimet ja niiden arvot. Juurelta voimme siirtyä solmuun ’a’ -> ’i’ -> ’r’. Tämä sekvenssi muodostaa sanan ”air”, jonka arvo (esimerkiksi se, kuinka monta kertaa tämä sana esiintyy tekstissä) on 4 (arvot ovat vihreän laatikon sisällä). Tavallisesti symbolitaulukon olemassa olevalla sanalla on arvo, joka ei ole nolla. Vaikka siis sana ”airway” on olemassa englanninkielisessä kielessä, se ei ole tässä kolmiossa, koska konvention mukaisesti avaimen ’y’ solmun arvo on nolla.
Sana ”air” on myös sanojen etuliite: ”airplane”; ja ”airways”. Sekvenssi ’h’ -> ’a’ muodostaa etuliitteen sanoille ”on” ja ”hattu”, kuten sekvenssi ’h’ -> ’o’ muodostaa etuliitteen sanoille ”talo” ja ”hevonen”.
Sen lisäksi, että se palvelee hyvin tietorakenteena vaikkapa sanakirjalle, se palvelee myös tärkeänä elementtinä täydennyssovelluksessa. Järjestelmä voisi ehdottaa sanoja ”airplane” ja ”airways” sen jälkeen, kun käyttäjä on kirjoittanut sanan ”air”, käymällä läpi alipuun, jonka juurena on solmu, jolla on avain ”r”. Tämän rakenteen lisähyöty on se, että ilman lisäkustannuksia voidaan saada järjestetty luettelo olemassa olevista avaimista kulkemalla kolmio järjestyksessä, pinoamalla solmun lapset ja kulkemalla niitä vasemmalta oikealle.
Kuvassa 2 on esimerkki solmun anatomiasta.

>
Kiinnostava piirre anatomiassa on se, että lapsien osoittimet tallennetaan tavallisesti matriisiin. Jos edustamme esimerkiksi Extended ASCII -merkkijoukkoa S, joukon on oltava kooltaan 256. Kun meillä on lapsen merkki, voimme käyttää sen osoitinta vanhemmassa merkissä O(1)-ajassa. Kun otetaan huomioon, että sanaston koko on N ja että pisimmän sanan koko on M, trion syvyys on myös M, ja rakenteen läpikäyminen kestää O(MN). Jos otetaan huomioon, että yleensä N on paljon suurempi kuin M (korpuksen sanojen määrä on paljon suurempi kuin pisimmän sanan koko), voidaan O(MN)-aikaa pitää lineaarisena. Käytännössä tämä joukko on harva, eli suurimmalla osalla solmuista on paljon vähemmän lapsia kuin S. Lisäksi sanojen keskimääräinen koko on myös pienempi kuin M, joten käytännössä avaimen etsimiseen kuluu keskimäärin O(logₛ N) ja koko rakenteen läpikäymiseen O(N logₛ N).
Tähän tietorakenteeseen liittyy kaksi pääongelmaa. Yksi on tilan kulutus. Jokaisella tasolla L, alkaen nollasta, on assimptoottisesti Sᴸ osoitinta. Jos Extended ASCII:n eli 256 merkin kohdalla tämä on ongelma rajallisissa muistilaitteissa, tilanne pahenee, jos otetaan huomioon kaikki Unicode-merkit (65 000 merkkiä). Toinen ongelma on sellaisten solmujen määrä, joissa on vain yksi lapsi, mikä heikentää syöttö- ja hakutulosten suorituskykyä. Kuvan 1 esimerkissä vain juurella, avaimella ”h” tasolla 1, avaimilla ”a” ja ”o” tasolla 2 ja avaimella ”r” tasolla 3 on enemmän kuin yksi lapsi. Toisin sanoen vain viidellä solmulla 27:stä on kaksi tai useampia lapsia. Vaihtoehdot tälle rakenteelle puuttuvat lähinnä näihin ongelmiin.
Ennen vaihtoehdon (PATRICIA Trie) kuvaamista vastaan seuraavaan kysymykseen: miksi vaihtoehtoja, jos voimme käyttää hash-taulukkoa joukon sijasta? Hash-taulukko todella auttaa säästämään muistia pienellä suorituskyvyn heikkenemisellä, mutta ei ratkaise ongelmaa. Mitä ylempänä trie:ssä ollaan (lähempänä tasoa nolla), sitä todennäköisemmin lähes kaikki merkit missä tahansa merkistösarjassa on käsiteltävä. Hyvin toteutetuissa hash-taulukoissa, kuten Javassa (ehdottomasti parhaiden joukossa, kiistatta paras), aloitetaan oletuskoolla ja kokoa muutetaan automaattisesti kynnysarvon mukaan. Javassa oletuskoko on 16 ja kynnysarvo 0,75, ja se kaksinkertaistaa kokonsa jokaisessa operaatiossa. Ottaen huomioon Extended ASCII, kun yhden solmun lapsiluku saavuttaa 192, hash-taulukon kokoa muutetaan 512:een, vaikka lopussa tarvitaan vain 256.
Radix Trie
Koska PATRICIA Trie on erikoistapaus Radix Triestä, aloitan jälkimmäisestä. Wikipediassa Radix Trie määritellään seuraavasti: ”tietorakenne, joka edustaa tilaoptimoitua kolmikkoa… jossa jokainen solmu, joka on ainoa lapsi, yhdistetään vanhempaansa… Toisin kuin tavallisissa puissa (joissa kokonaisia avaimia verrataan massoittain niiden alusta epätasa-arvoon asti), avainta verrataan jokaisessa solmussa bitti kerrallaan, jolloin bittien määrä kyseisessä bittipalassa kyseisessä solmussa on radix-trion radix r”. Määritelmästä tulee ymmärrettävämpi, kun kuvaamme tätä triestä esimerkkinä kuvassa 3.
Solmun lasten lukumäärä r radix-triessä määräytyy seuraavan kaavan mukaan, jossa x on edellä mainitun chunk-of-bitsin vertailuun tarvittavien bittien lukumäärä:
Yllä olevan kaavan mukaan radix-triessä lasten lukumäärä on aina 2:n monikerta. Esimerkiksi 4-Radix Trie:n tapauksessa x = 2. Tämä tarkoittaa, että meidän olisi verrattava kahden bitin kappaleita, bittiparia, koska näillä kahdella bitillä esitämme kaikki desimaaliluvut 0:sta 3:een, eli yhteensä 4 eri lukua, yksi jokaiselle lapselle.
Ylläolevien määritelmien paremman ymmärtämisen vuoksi tarkastellaan kuvan 3 esimerkkiä. Tässä esimerkissä meillä on hypoteettinen merkkijoukko, joka koostuu viidestä merkistä (NULL, A, B, C ja D). Päätin esittää ne käyttämällä vain 4 bittiä (muistakaa, että tällä ei ole mitään tekemistä r:n kanssa, sillä viiden merkin esittämiseen tarvitaan vain 3 bittiä, vaan se liittyy esimerkin piirtämisen helppouteen). Kuvion vasemmassa yläkulmassa on taulukko, joka kuvaa kunkin merkin bittimuotoista esitystä.
Voidakseni lisätä merkin ’A’, vertaan sitä bittikohtaisesti NULL-merkkiin. Kuvan 3 oikeassa yläkulmassa, keltaisella timantilla 1 merkityssä laatikossa, näemme, että nämä kaksi merkkiä eroavat toisistaan ensimmäisen parin kohdalla. Tämä ensimmäinen pari on esitetty punaisella A:n 4-bittisessä esityksessä. DIFF sisältää siis bittipaikan, jossa erilainen pari päättyy.
Lisätäksemme merkin ’B’ meidän on verrattava sitä biteittäin merkkiin ’A’. Tämä vertailu on timanttilaatikossa, joka on merkitty merkillä 2. Ero osuu tällä kertaa toiseen, punaisella merkittyyn bittipariin, joka päättyy kohtaan 4. Koska toinen pari on 01, luomme solmun, jolla on avain B, ja osoitamme siihen solmun A osoitteen 01. Tämä linkki näkyy kuvan 3 alaosassa.
Tämän esimerkin tarkoituksena on kuvata edellä esitetyssä Radix Trie -määritelmässä mainittua chunk-of-bits-vertailua, tilan optimointia (tässä tapauksessa vain neljä lasta riippumatta merkkijoukon koosta) ja vanhempien ja lasten yhdistämistä (lapsisolmuun tallennetaan vain ne bitit, jotka eroavat juuresta). Siitä huolimatta on edelleen yksi linkki, joka osoittaa nollasolmuun. Sparseness on suoraan verrannollinen r:ään ja trien syvyyteen.
PATRICIA Trie
PATRICIA (Practical Algorithm to Retrieve Information Coded in Alphanumeric (Käytännön algoritmi aakkosnumeerisesti koodatun tiedon hakemiseen, Journal of the ACM, 15(4):514-534, lokakuu 1968) . Kyllä, PATRICIA on lyhenne!
PATRICIA Trie määritellään tässä kolmella säännöllä:
- Kullakin solmulla (TWIN on PATRICIAn alkuperäinen termi) on kaksi lasta (r = 2 ja x = 1 Radix Trie -termeissä);
- Solmu jakautuu vain etuliitteeksi (L-PHRASE PATRICIAn termeissä), jolla on kaksi lasta (kukin lapsi muodostaa BRANCHin, joka on PATRICIAn alkuperäinen termi), jos kahdella sanalla (PROPER OCCURRENCE PATRICIAn termeissä) on sama etuliite; ja
- Jokainen sanan loppu esitetään solmun sisällä arvolla, joka on eri kuin nolla (END-merkki PATRICIAN alkuperäisessä nomenklatuurissa)
Sääntö numero 2 edellä edellyttää, että etuliitteen pituus kullakin tasolla on suurempi kuin edellisen tason etuliitteen pituus. Tämä on erittäin tärkeää algoritmeissa, jotka tukevat PATRICIA-operaatioita, kuten elementin lisäämistä tai toisen elementin etsimistä.
Yllä olevien sääntöjen perusteella voidaan määritellä solmu alla esitetyllä tavalla. Jokaisella solmulla on juurta lukuun ottamatta yksi vanhempi ja kaksi lasta, arvo (minkä tahansa tyyppinen) ja muuttuja diff, joka ilmaisee sijainnin, jossa jako on avaimen bittikoodissa

Käyttääksemme PATRICIA-algoritmia tarvitsemme funktiota, joka palauttaa kahden merkkijonon annettuna sen ensimmäisen bitin sijainnin vasemmalta oikealle, jossa ne eroavat toisistaan. Näimme jo tämän toimivan Radix Trie:n kohdalla.
Käyttääksemme trie:tä PATRICIA:n avulla, eli lisätäksemme tai löytääksemme siihen avaimia, tarvitsemme 2 osoitinta. Yksi on parent, joka alustetaan osoittamalla se juurisolmuun. Toinen on child, joka alustetaan osoittamalla se juuren vasempaan lapseen.
Jatkossa muuttuja diff pitää sisällään paikan, jossa lisättävä avain eroaa child.key:stä. Säännön numero 2 mukaisesti määrittelemme seuraavat kaksi epäyhtälöä:
Let found osoittaa solmuun, johon avaimen etsintä päättyy. Jos found.key eroaa syötettävästä merkkijonosta, diff lasketaan ComputeDiff-funktion avulla käyttäen tätä merkkijonoa ja found.key:tä. Jos ne ovat samat, avain on olemassa rakenteessa, ja kuten missä tahansa symbolitaulukossa, arvo on palautettava. Operaatioissa käytetään apumetodia nimeltä BitAtPosition, joka hakee bitin tietyssä kohdassa (0 tai 1).
Hakua varten on määriteltävä funktio Search(key). Sen pseudokoodi on kuvassa 4.

Toiseksi funktioksi, jota käytämme tässä tarinassa, tulee Insert(key). Sen pseudokoodi on kuvassa 6.

Ylläolevassa pseudokoodissa on metodi solmun luomiseksi nimeltä CreateNode. Sen argumentit voidaan ymmärtää kuvasta 4.
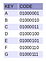
Vaikuttaakseni esimerkkinä siitä, miten PATRICIA Trie toimii, opastan lukijaa mieluummin vaihe vaiheelta suorittamaan 7 merkin (’A’, ’B’, ’C’, ’D’, ’E’, ’F’ ja ’G’, kuten kuvassa 7 viereisessä kuvassa on määritelty) lisäämisen niiden luonnollisessa järjestyksessä. Lopulta on toivottavasti ymmärretty, miten tämä tietorakenne toimii.
Merkki A lisätään ensimmäisenä. Sen bittikoodi on 01000001. Kuten Radix Trie:ssä, vertaamme tätä bittikoodia juuressa olevaan bittikoodiin, joka tällä hetkellä on nolla, eli vertaamme 00000000:a 01000001:een. Ero putoaa kohtaan 2 (tässä, koska x = 1, vertaamme bitti kerrallaan parin sijasta).

Luodaksemme solmun meidän on osoitettava vasemmalle ja oikealle lapselle niiden seuraajat. Koska tämä solmu on juuri, sen vasen lapsi osoittaa määritelmän mukaan itseensä, kun taas sen oikea lapsi osoittaa nollaan. Tästä tulee koko kolmion ainoa nollaosoitin. Muistetaan, että juuri on ainoa solmu, jolla ei ole vanhempaa. Arvo, joka esimerkissämme on kokonaisluku, joka jäljittelee sananlaskentasovellusta , asetetaan arvoon 1. Tämän lisäysoperaation tulos näkyy kuvassa 8.
Seuraavaksi lisätään merkki B, jonka bittikoodi on 01000010. Ensimmäiseksi tarkistetaan, onko tämä merkki jo rakenteessa. Tätä varten etsimme sen. Haku PATRICIA-triessä on yksinkertaista (katso pseudokoodi kuvassa 5). Kun juuren avainta on verrattu B:hen, voidaan päätellä, että ne ovat erilaiset, joten jatketaan luomalla kaksi osoitinta: vanhempi ja lapsi. Aluksi parent osoittaa juureen ja child osoittaa juuren vasempaan lapseen. Tässä tapauksessa molemmat osoittavat solmuun A. Säännön numero 2 mukaisesti iteroimme rakennetta, kun epäyhtälö (1) on tosi.
Tällä hetkellä parent.DIFF on yhtä suuri kuin child.DIFF eikä pienempi kuin child.DIFF. Tämä rikkoo epäyhtälön (1). Koska child.VALUE on eri kuin null (yhtä suuri kuin 1), vertaamme merkkejä. Koska A on eri kuin B, tämä tarkoittaa, että B ei ole trieessä ja se on lisättävä.
Sisällyttämiseksi aloitamme jälleen määrittelemällä vanhemman ja lapsen kuten ennenkin, eli vanhempi osoittaa juurta ja lapsi osoittaa sen vasenta solmua. Rakenteen läpi iteroinnin on noudatettava epäyhtälöitä (1) ja (2). Jatketaan laskemalla diff, joka on B:n ja child.KEY:n bittien välinen erotus, joka tässä vaiheessa on yhtä suuri kuin A (bittikoodien 01000001 ja 01000010 välinen erotus) . Ero osuu bittiin paikassa 7 , joten diff = 7.

Tällä hetkellä vanhempi (parent) ja lapsi (child) osoittavat samaan solmupisteeseen (solmupisteeseen A, juureen). Koska epäyhtälö (1) on jo epätosi ja child.DIFF on pienempi kuin diff, luomme solmun B ja osoitamme parent.LEFT siihen. Kuten teimme solmun A kanssa, meidän on osoitettava solmun B lapset jonnekin. B:n kohdassa 7 oleva bitti on 1, joten solmun B oikea lapsi osoittaa itseensä. Solmun B vasen lapsi osoittaa vanhempaan, tässä tapauksessa juureen. Lopputulos on esitetty kuvassa 9.
Osoittamalla solmun B vasen lapsi vanhempaansa mahdollistamme säännössä 2 mainitun jaon. Kun lisäämme merkin, jonka diff on 2:n ja 7:n välissä, tämä osoitin lähettää meidät takaisin oikeaan paikkaan, josta uusi merkki lisätään. Näin tapahtuu, kun lisäämme merkin D.
Mutta sitä ennen meidän on lisättävä merkki C, jonka bittikoodi on 01000011. Osoitin parent osoittaa solmuun A (juuri). Tällä kertaa, toisin kuin etsiessämme merkkiä B, lapsi osoittaa solmuun B (tuolloin molemmat osoittimet osoittivat juurta).
Tällä hetkellä epäyhtälö (1) pätee (parent.DIFF on pienempi kuin child.DIFF), joten päivitämme molemmat osoittimet asettaen parentin lapseksi ja lapsen solmun B oikeaksi lapseksi, koska paikassa 7 C:n bitti on 1.
Päivittämisen jälkeen kumpikin osoitin osoittaa solmuun B rikkoen epäyhtälön (1). Kuten aiemmin, vertaamme child.KEY-bittikoodia ja C:n bittikoodia (01000010 ja 01000011) ja tulemme siihen tulokseen, että ne eroavat toisistaan kohdassa 8. Koska paikassa 7 C:n bitti on 1, tämä uusi solmu (solmu C) on B:n oikeanpuoleinen lapsi. Paikassa 8 C:n bitti on 1, mikä saa meidät asettamaan solmun C oikeanpuoleisen lapsen itselleen, kun taas sen vasemmanpuoleinen lapsi osoittaa vanhempaan, solmuun B tällä hetkellä. Tuloksena syntyvä trie on kuvassa 10.

Seuraava merkki on D (bittikoodi 01000100). Kuten teimme merkin C lisäämisessä, asetamme aluksi osoittimen parent solmuun A ja osoittimen child solmuun B. Epäyhtälö (1) on voimassa, joten päivitämme osoittimet. Nyt parent osoittaa solmuun B ja child osoittaa solmun B vasempaan lapseen, koska kohdassa 7 D:n bitti on 0. Toisin kuin merkin C lisääminen, nyt child osoittaa takaisin solmuun A, mikä rikkoo epäyhtälön (1). Lasketaan jälleen A:n ja D:n bittikoodien erotus. Nyt diff on 6. Asetamme taas vanhemman ja lapsen kuten normaalisti. Nyt kun epäyhtälö (1) on voimassa, epäyhtälö (2) ei ole. Tästä seuraa, että lisäämme D:n A:n vasemmaksi lapseksi. Mutta entä D:n lapset? Paikassa 6 D:n bitti on 1, joten sen oikea lapsi osoittaa itseensä. Mielenkiintoista on, että solmun D vasen lapsi osoittaa nyt solmuun B saavuttaen kuvaan 11 piirretyn kolmion.

Seuraavana on merkki E, jonka bittikoodi 01000101. Haku-toiminto palauttaa solmun D. Merkkien D ja E välinen ero osuu bittiin paikassa 8. Koska paikassa 6 E:n bitti on 1, se sijoitetaan D:n oikealle puolelle. Trion rakenne on esitetty kuvassa 12.

Mielenkiintoista merkin F lisäämisessä on se, että sen paikka on merkkien D ja E välissä, koska D:n ja F:n erotus on paikassa 7. Merkin F paikka on D:n ja F:n välillä. Mutta paikassa 7 E:n bitti on 0, joten solmu E on solmun F vasen lapsi. Rakenne on nyt esitetty kuvassa 13.

Viimeiseksi lisäämme merkin G. Kaikkien laskutoimitusten jälkeen tulemme siihen johtopäätökseen, että uusi solmu tulee sijoittaa solmun F oikeanpuoleiseksi lapseksi, jonka diff on 8. Lopputulos on kuvassa 14.

Tähän asti olemme lisänneet merkkijonoja, jotka koostuvat vain yhdestä merkistä. Mitä tapahtuisi, jos wit yrittäisi lisätä merkkijonoja AB ja BA? Kiinnostunut lukija voi ottaa tämän lauseen harjoitustehtäväksi. Kaksi vihjettä: molemmat merkkijonot eroavat solmun B kohdasta 9; ja lopullinen trie on esitetty kuvassa 15.

Viimeistä kuviota tarkasteltaessa voidaan kysyä seuraavaa: Löytääkseen esimerkiksi merkkijonon BA tarvitaan 5 bittivertailua, kun taas tämän merkkijonon hash-koodin laskemiseen tarvitaan vain kaksi iteraatiota, joten milloin PATRICIA Trie tulee kilpailukykyiseksi? Kuvitellaan, että tähän rakenteeseen lisätään merkkijono ABBABABBBBABABABBA (joka on peräisin PATRICIAn alkuperäisen artikkelin esimerkistä vuodelta 1968), joka on 16 merkkiä pitkä. Tämä merkkijono sijoitettaisiin solmun AB vasemmanpuoleiseksi lapseksi solmun diff sijalle 17. Sen löytämiseksi tarvitsisimme 5 bittivertailua, kun taas hash-koodin laskeminen vaatisi 16 iteraatiota, yhden jokaiselle merkille, ja tästä syystä PATRICIA Trie on niin kilpailukykyinen etsittäessä pitkiä merkkijonoja.
PATRICIA Trie vs. Hash Map
Tässä viimeisessä osiossa vertailen Hash Mapia ja PATRICIA Triea kahdessa sovelluksessa. Ensimmäinen on sanojen laskeminen leipzig1m.txt-tiedostossa, joka sisältää miljoona satunnaista lausetta, ja toinen on symbolitietotaulukon täyttäminen yli 2,3 miljoonalla URL-osoitteella DMOZ-projektista (suljettu vuonna 2017), joka on ladattu täältä.
Koodi, jonka kehitin ja jota käytin sekä yllä olevan pseudokoodin toteuttamiseen että PATRICIA Trien suorituskyvyn vertailemiseen Hash-taulukon suorituskykyyn, on löydettävissä GitHubissani.
Nämä vertailut ajettiin Ubuntu-levyni Ubuntu-laatikossa (Ubuntu-laatikossa). Konfiguraatio löytyy kuvasta 16
.