A mikrovilágban, ahová be vagyok ágyazva, a trie adatstruktúra nem olyan népszerű. Ez a környezet főleg adattudósokból és kisebb számban szoftvermérnökökből áll, akik természetes nyelvfeldolgozással (NLP) foglalkoznak.
A közelmúltban egy érdekes vitában találtam magam arról, hogy mikor használjunk trie-t vagy hash-táblát. Bár ebben a vitában nem volt semmi újdonság, amiről itt beszámolhatnék, mint például a két adatszerkezet előnyei és hátrányai (ha egy kicsit guglizol, sok linket találsz, ami ezekkel foglalkozik), ami új volt számomra, az a trie egy speciális típusa, az úgynevezett Patricia Trie, és az, hogy bizonyos forgatókönyvekben ez az adatszerkezet mind feldolgozási időben, mind térben összehasonlíthatóan jobban teljesít a hash táblával, miközben olyan feladatokat old meg, mint a közös előtaggal rendelkező karakterláncok listázása plusz költség nélkül.
Ezt szem előtt tartva kerestem egy olyan történetet vagy blogot, amely segít egyszerű módon (a lustaság eufemizmusa) megérteni, hogyan működik a PATRICIA algoritmus, kifejezetten rövidítésként szolgálva az 1968-ban megjelent 21 oldalas tanulmány elolvasásához. Sajnos nem jártam sikerrel ebben a keresésben, így nem maradt más választásom, mint elolvasni.
Ezzel a történettel az a célom, hogy betöltsem a fenti hiányt, azaz legyen egy történet, amely laikus nyelven leírja a szóban forgó algoritmust.
A célom elérése érdekében először is röviden és tömören bemutatom, a próbálkozásokban nem járatosak számára, ezt az adatszerkezetet. Ezt a bevezetést követően felsorolom a legnépszerűbb trie-ket, amelyek lehetővé teszik számomra, hogy megvalósítsam és részletesen leírjam, hogyan működik a PATRICIA Trie, és miért teljesítenek olyan jól. A történet végén összehasonlítom az eredményeket (teljesítmény és helyfogyasztás) két különböző alkalmazásban: az első egy szószámlálás (<WORD, FREQUENCY> tuples) egy meglehetősen nagy szöveg alapján; a második pedig egy <URL, IP> tuples felépítése, egy több mint 2 millió URL-t tartalmazó lista alapján, amely egy DNS-kiszolgáló központi eleméből áll. Mindkét alkalmazás Hash Map és Patricia Trie alapján készült.
Az Algorithms – Fourth Edition című könyvükben (kiadó: Addison-Wesley) Sedgewick és Wayne (Princeton University) meghatározása szerint a trie vagy prefix tree “a keresőkulcs karaktereiből felépített adatszerkezet, amely a keresést irányítja”. Ez az “adatszerkezet csomópontokból áll, amelyek olyan hivatkozásokat tartalmaznak, amelyek vagy nullák, vagy más csomópontokra hivatkoznak. Minden csomópontra csak egy másik csomópont mutat, amelyet szülőnek nevezünk (kivéve egy csomópontot, a gyökeret, amelyre nem mutatnak csomópontok), és minden csomópontnak S linkje van, ahol S az ábécé (vagy betűkészlet) mérete”.
A fenti definíciót követő alábbi 1. ábra egy trie példáját tartalmazza.

A gyökér csomópontnak nincs címkéje. Három gyermeke van: “a”, “h” és “s” kulcsú csomópontok. Az ábra jobb alsó sarkában egy táblázat található, amely felsorolja az összes kulcsot a hozzájuk tartozó értékkel. A gyökérből az ‘a’ -> ‘i’ -> ‘r’ csomópontok felé haladhatunk. Ez a szekvencia alkotja a “levegő” szót, amelynek értéke (például az, hogy ez a szó hányszor fordul elő a szövegben) 4 (az értékek egy zöld dobozban vannak). Egyezmény szerint a szimbólumtáblában egy létező szónak nem nulla értéke van. Tehát, bár az angolban létezik a “airway” szó, ebben a trie-ben nem szerepel, mert a konvenciót követve az “y” kulcsú csomópont értéke nulla.
A “air” szó egyben a szavak előtagja is: “airplane”; és “airways”. A ‘h’ -> ‘a’ szekvencia képezi a “van” és a “kalap” előtagját, ahogy a ‘h’ -> ‘o’ szekvencia képezi a “ház” és a “ló” előtagját.
Mellett, hogy jól szolgál, mondjuk, egy szótár adatszerkezeteként, egy kitöltő alkalmazás fontos elemeként is. Egy rendszer javasolhatná a “repülőgép” és a “légutak” szavakat, miután a felhasználó beírta a “levegő” szót, azáltal, hogy bejárja azt a részfát, amelynek gyökere az “r” kulcsú csomópont. Ennek a struktúrának további előnye, hogy további költség nélkül kaphatunk egy rendezett listát a létező kulcsokról, ha a trie-t rendezett irányban haladva, egy csomópont gyermekeit egymásra halmozva, balról jobbra haladva haladunk rajta.
A 2. ábrán a csomópont anatómiáját szemléltetjük.

Az anatómia érdekessége, hogy a gyermekmutatókat általában egy tömbben tároljuk. Ha egy S karakterkészletet reprezentálunk, például Extended ASCII-t, akkor a tömbnek 256 méretűnek kell lennie. Egy gyermekkarakter birtokában O(1) idő alatt elérhetjük a szülőben lévő mutatóját. Ha figyelembe vesszük, hogy a szókincs mérete N, és hogy a leghosszabb szó mérete M, a trie mélysége szintén M, és a struktúra bejárása O(MN) időt vesz igénybe. Ha figyelembe vesszük, hogy általában N sokkal nagyobb, mint M (a korpuszban lévő szavak száma sokkal nagyobb, mint a leghosszabb szó mérete), akkor O(MN) lineárisnak tekinthető. A gyakorlatban ez a tömb ritka, azaz a csomópontok többségének sokkal kevesebb gyermeke van, mint S. Ráadásul a szavak átlagos mérete is kisebb, mint M, így a gyakorlatban átlagosan O(logₛ N) szükséges egy kulcs kereséséhez és O(N logₛ N) a teljes struktúra bejárásához.
Ezzel az adatstruktúrával két fő probléma van. Az egyik a helyfogyasztás. Minden L szinten, kezdve a nullával, asszimptotikusan Sᴸ mutató van. Ha az Extended ASCII, azaz 256 karakter esetén ez korlátozott memóriájú eszközökön problémát jelent, akkor a helyzet tovább romlik, ha az összes Unicode karaktert (65.000 karaktert) figyelembe vesszük. A második a csak egy gyermekkel rendelkező csomópontok mennyisége, ami rontja a beviteli és keresési teljesítményt. Az 1. ábrán látható példában csak a gyökér, a “h” kulcs az 1. szinten, az “a” és “o” kulcsok a 2. szinten és az “r” kulcs a 3. szinten rendelkezik egynél több gyermekkel. Más szóval a 27 csomópontból csak 5 csomópontnak van két vagy több gyermeke. Ennek a struktúrának az alternatívái elsősorban ezeket a problémákat kezelik.
Az alternatíva (PATRICIA Trie) ismertetése előtt a következő kérdésre válaszolok: miért alternatívák, ha tömb helyett hash-táblát is használhatunk? A hashtábla valóban segít a memória megtakarításában kis teljesítménycsökkenés mellett, de nem oldja meg a problémát. Minél feljebb vagyunk a trie-ben (közelebb a nulladik szinthez), annál valószínűbb, hogy bármelyik karakterkészletben szinte minden karaktert kezelni kell. A jól megvalósított hash-táblák, mint például a Java-ban található (egyértelműen a legjobbak közé tartozik, vitathatatlanul a legjobb), egy alapértelmezett mérettel kezdődnek, és automatikusan átméreteződnek egy küszöbértéknek megfelelően. A Java-ban az alapértelmezett méret 16, 0,75-ös küszöbértékkel, és minden egyes műveletnél megduplázza a méretét. Az Extended ASCII-t figyelembe véve, mire egy csomópontban a gyerekek száma eléri a 192-t, a hash-tábla mérete 512-re változik, pedig a végén csak 256-ra van szüksége.
Radix Trie
Mivel a PATRICIA Trie a Radix Trie egy speciális esete, az utóbbival kezdem. A Wikipédiában a Radix Trie-t a következőképpen definiálják: “egy olyan adatszerkezet, amely egy téroptimalizált trie-t reprezentál… amelyben minden olyan csomópont, amely az egyetlen gyermek, összevonásra kerül a szülőjével… A hagyományos fákkal ellentétben (ahol az egész kulcsokat tömegesen hasonlítják össze a kezdetüktől az egyenlőtlenség pontjáig), a kulcsot minden csomópontban bitdarabról bitdarabra hasonlítják össze, ahol az adott csomópontban lévő bitek mennyisége a radix r a radix trie-ban”. Ennek a definíciónak több értelme lesz, ha ezt a trie-t a 3. ábrán szemléltetjük.
Egy csomópont r gyermekeinek számát egy radix trie-ben a következő képlettel határozzuk meg, ahol x a fent említett chunk-of-bits összehasonlításához szükséges bitek száma:
A fenti képlet szerint a radix trie gyermekeinek száma mindig 2 többszöröse. Például egy 4-Radix Trie esetében x = 2. Ez azt jelenti, hogy két bitből álló darabokat, egy bitpárt kellene összehasonlítanunk, mert ezzel a két bit-tel ábrázoljuk az összes tizedes számot 0-tól 3-ig, összesen 4 különböző számot, minden gyermekhez egyet.
A fenti definíciók jobb megértéséhez nézzük meg a 3. ábrán látható példát. Ebben a példában van egy feltételezett karakterkészletünk, amely 5 karakterből áll (NULL, A, B, C és D). Úgy döntöttem, hogy ezeket csak 4 bit felhasználásával ábrázolom (ne feledjük, hogy ennek semmi köze az r-hez, 5 karakter ábrázolásához csak 3 bitre van szükség, hanem a példa egyszerűbb megrajzolhatóságához). Az ábra bal felső sarkában van egy táblázat, amely az egyes karaktereket a bitreprezentációjukhoz rendeli.
Az ‘A’ karakter beillesztéséhez bitenként összehasonlítom a NULL karakterrel. A 3. ábra jobb felső sarkában, a sárga rombuszban 1-gyel jelölt dobozon belül láthatjuk, hogy ez a két karakter az első párnál különbözik. Ezt az első párt piros színnel ábrázoljuk A 4 bites ábrázolásában. A DIFF tehát azt a bitpozíciót tartalmazza, ahol az eltérő pár véget ér.
A ‘B’ karakter beillesztéséhez bitenként kell összehasonlítanunk az ‘A’ karakterrel. Ez az összehasonlítás a 2-vel jelölt rombuszdobozban van. A különbség ezúttal a piros színnel jelölt második bitpárra esik, amely a 4-es pozícióban végződik. Mivel a második pár 01, létrehozzuk a B kulcsú csomópontot, és az A csomópontban lévő 01-es címre mutatunk rá. Ez a kapcsolat a 3. ábra alsó részén látható. Ugyanez az eljárás vonatkozik a “C” és “D” karakterek beszúrására is.

A fenti példában látható, hogy az első pár (01 kékkel) az összes beszúrt karakter előtagja.
Ez a példa a fenti Radix Trie definícióban említett chunk-of-bits összehasonlítás, a helyoptimalizálás (ebben az esetben csak négy gyerek, függetlenül a karakterkészlet méretétől) és a szülő-gyerek egyesítés (a gyerek csomópontokban csak a gyökértől eltérő biteket tároljuk) leírására szolgál. Ennek ellenére még mindig van egy link, amely egy null csomópontra mutat. A ritkaság egyenesen arányos az r-rel és a trie mélységével.
PATRICIA Trie
PATRICIA (Practical Algorithm to Retrieve Information Coded in Alphanumeric, Journal of the ACM, 15(4):514-534, October 1968) . Igen, a PATRICIA egy rövidítés!
A PATRICIA trie-t itt három szabály határozza meg:
- Minden csomópontnak (TWIN az eredeti PATRICIA kifejezés) két gyermeke van (r = 2 és x = 1 a Radix Trie kifejezésekben);
- Egy csomópont csak akkor oszlik fel egy előtagra (L-PHRASE a PATRICIA kifejezésekben) két gyermekkel (mindegyik gyermek egy BRANCH-ot alkot, amely a PATRICIA eredeti kifejezés), ha két szó (PROPER OCCURRENCE a PATRICIA kifejezésekben) osztozik ugyanazon az előtagon; és
- Minden szóvéget a csomóponton belül a nullától (END jel a PATRICIA eredeti nómenklatúrájában)
A fenti 2. szabály azzal jár, hogy az előtag hossza minden szinten nagyobb, mint az előző szint előtagjának hossza. Ez nagyon fontos lesz a PATRICIA műveleteket támogató algoritmusokban, mint például egy elem beillesztése vagy egy másik keresése.
A fenti szabályok alapján a csomópontot az alábbi ábrán látható módon definiálhatjuk. Minden csomópontnak van egy szülője, kivéve a gyökeret, és két gyermeke, egy érték (bármilyen típusú) és egy változó diff, amely azt a pozíciót jelzi, ahol az osztás a kulcs bitkódjában van

A trie működtetéséhez a PATRICIA segítségével, azaz a kulcsok beszúrásához vagy megtalálásához 2 mutatóra van szükségünk. Az egyik a parent, amelyet úgy inicializálunk, hogy a gyökércsomópontra mutatunk. A másik a child, amelyet a root bal oldali gyermekére mutatva inicializálunk.
A következőkben a diff változó fogja tartani azt a pozíciót, ahol a beszúrandó kulcs eltér a child.key-től. A 2. számú szabályt követve definiáljuk a következő 2 egyenlőtlenséget:
Let found arra a csomópontra mutat, ahol a kulcs keresése véget ér. Ha a found.key különbözik a beillesztendő karakterlánctól, a diff kiszámításra kerül a ComputeDiff függvényen keresztül, ennek a karakterláncnak és a found.key-nek a felhasználásával. Ha ezek megegyeznek, akkor a kulcs létezik a struktúrában, és mint minden szimbólumtáblában, az értéket kell visszaadni. A műveletek során egy BitAtPosition nevű segédmetódust fogunk használni, amely egy adott pozícióban (0 vagy 1) lévő bitet kérdez ki.
A kereséshez definiálnunk kell egy Search(key) függvényt. Ennek pszeudokódja a 4. ábrán látható.

A második függvény, amelyet ebben a történetben használni fogunk, az Insert(kulcs). Pszeudokódja a 6. ábrán látható.

A fenti pszeudokódban van egy CreateNode nevű metódus egy csomópont létrehozására. Ennek argumentumai a 4. ábrából érthetők meg.
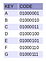
A PATRICIA Trie működésének szemléltetésére inkább egy lépésről-lépésre történő műveletbe vezetem az olvasót, hogy 7 karakter (‘A’, ‘B’, ‘C’, ‘D’, ‘E’, ‘F’ és ‘G’ a 7. ábra mellett megadottak szerint) természetes sorrendben történő beillesztését elvégezze. A végén remélhetőleg megértettük, hogyan működik ez az adatszerkezet.
Az A karakter az első, amelyet be kell illeszteni. Bitkódja 01000001. Mint a Radix Trie esetében, ezt a bitkódot is összehasonlítjuk a gyökérnél lévővel, amely ebben a pillanatban nulla, tehát a 00000000-at a 01000001-gyel hasonlítjuk össze. A különbség a 2. pozícióba esik (itt, mivel x = 1, bitenként hasonlítjuk össze a bitpár helyett).

A csomópont létrehozásához a bal és jobb oldali gyermekre kell mutatnunk a megfelelő utódokra. Mivel ez a csomópont a gyökér, a definíció szerint a bal oldali gyermeke önmagára, míg a jobb oldali gyermeke a nullára mutat. Ez lesz az egyetlen null mutató az egész trie-ben. Ne feledjük, hogy a gyökér az egyetlen olyan csomópont, amelynek nincs szülője. Az értéket, a mi példánkban egész számok lesznek egy szószámláló alkalmazást utánozva , 1-re állítjuk. Ennek a beszúrási műveletnek az eredménye a 8. ábrán látható.
A következőkben B karaktert fogunk beszúrni a 01000010-es bitkóddal. Először is ellenőrizzük, hogy ez a karakter már szerepel-e a struktúrában. Ehhez megkeressük. A PATRICIA Trie-ben való keresés egyszerű (lásd az 5. ábrán látható pszeudokódot). A gyökér és B kulcsának összehasonlítása után arra a következtetésre jutunk, hogy ezek különböznek, így 2 mutató létrehozásával folytatjuk: szülő és gyermek. Kezdetben a parent a gyökérre mutat, a child pedig a gyökér bal oldali gyermekére. Ebben az esetben mindkettő az A csomópontra mutat. A 2. számú szabályt követve addig iteráljuk a struktúrát, amíg az (1) egyenlőtlenség igaz.
Ebben a pillanatban a parent.DIFF egyenlő és nem kisebb, mint a child.DIFF. Ez megtöri az (1) egyenlőtlenséget. Mivel a child.VALUE különbözik a nullától (egyenlő 1), összehasonlítjuk a karaktereket. Mivel A különbözik B-től, ez azt jelenti, hogy B nincs a trie-ben, és be kell illeszteni.
A beillesztéshez újra elkezdjük a parent és a child meghatározását, mint korábban, azaz a parent a gyökérre, a child pedig annak bal oldali csomópontjára mutat. A struktúrán való iterációnak az (1) és (2) egyenleteket kell követnie. A diff kiszámításával folytatjuk, amely a B és a child.KEY közötti bitenkénti különbség, amely ebben a szakaszban egyenlő A-val (01000001 és 01000010 bitkódok közötti különbség) . A különbség a 7-es pozícióban lévő bitre esik , tehát diff = 7.

Ebben a pillanatban a szülő és a gyermek ugyanarra a csomópontra mutat (az A csomópontra, a gyökérre). Mivel az (1) egyenlőtlenség már hamis, és a child.DIFF kisebb, mint a diff, létrehozzuk a B csomópontot, és a parent.LEFT erre mutat. Ahogy az A csomópont esetében is tettük, a B csomópont gyermekeit is rá kell mutatnunk valahová. A B csomópontban a 7. pozícióban lévő bit 1, így a csomópont B jobb oldali gyermeke önmagára fog mutatni. A csomópont B bal oldali gyermeke a szülőre, ebben az esetben a gyökérre fog mutatni. A végeredmény a 9. ábrán látható.
Azzal, hogy a csomópont B bal oldali gyermekét a szülőre mutatjuk, lehetővé tesszük a 2. szabályban említett felosztást. Amikor olyan karaktert illesztünk be, amelynek diff-je 2 és 7 közé esik, ez a mutató vissza fog küldeni minket a megfelelő helyre, ahonnan az új karaktert beillesztjük. Ez akkor fog megtörténni, amikor D karaktert illesztünk be.
De előtte be kell illesztenünk a C karaktert, amelynek bitkódja 01000011. A szülő mutató az A csomópontra (a gyökérre) fog mutatni. Ezúttal, másképp, mint amikor a B karaktert kerestük, a gyermek a B csomópontra mutat (akkor mindkét mutató a gyökérre mutatott).
Ebben a pillanatban az (1) egyenlőtlenség érvényes (a parent.DIFF kisebb, mint a child.DIFF), ezért mindkét mutatót frissítjük, a parentet a gyermekre, a gyermeket pedig a B csomópont jobb oldali gyermekére állítva, mert a 7. pozícióban C bitje 1.
A frissítés után mindkét mutató a B csomópontra mutat, ezzel az (1) egyenlőtlenséget felbontva. Ahogy korábban is tettük, összehasonlítjuk a child.KEY bitkódot a C bitkódjával (01000010 a 01000011-gyel), és arra a következtetésre jutunk, hogy a 8. pozícióban különböznek. Mivel a 7. pozícióban C bitje 1, ez az új csomópont (C csomópont) lesz B jobb oldali gyermeke. A 8. pozícióban C bitje 1, így a C csomópont jobb oldali gyermekét önmagára állítjuk, míg bal oldali gyermeke ebben a pillanatban a szülőre, B csomópontra mutat. Az így kapott trie a 10. ábrán látható.

A következő karakter a D (bitkód 01000100). Ahogyan a C karakter beszúrásánál tettük, kezdetben a szülő mutatót az A csomópontra, a gyermek mutatót pedig a B csomópontra állítjuk. Az (1) egyenlőtlenség érvényes, tehát frissítjük a mutatókat. Most a szülő a B csomópontra mutat, a gyermek pedig a B csomópont baloldali gyermekére, mivel a 7. pozícióban a D bit 0. A C karakter beszúrásától eltérően most a gyermek visszamutat az A csomópontra, felbontva az (1) egyenlőtlenséget. Ismét kiszámítjuk az A és D bitkódok közötti különbséget. Most a diff 6. Ismét a szokásos módon állítjuk be a szülőt és a gyermeket. Most, míg az (1) egyenlőtlenség érvényes, a (2) egyenlőtlenség nem. Ez azt vonja maga után, hogy D-t A bal oldali gyermekeként fogjuk beilleszteni. De mi a helyzet D gyermekeivel? A 6. pozícióban D bitje 1, tehát jobb oldali gyermeke önmagára mutat. Az érdekes az, hogy a csomópont D bal oldali gyermeke most a B csomópontra fog mutatni, elérve a 11. ábrán kirajzolódó trie-t.

A következő az E karakter a 01000101 bitkóddal. A Keresés funkció a D csomópontot adja vissza. A D és E karakterek közötti különbség a 8. pozícióban lévő bitre esik. Mivel a 6. pozícióban E bitje 1, ezért D-től jobbra fog elhelyezkedni. A trie struktúráját a 12. ábra szemlélteti.

Az F karakter beszúrásának érdekessége, hogy a helye a D és E karakterek közé kerül, mivel a D és F közötti különbség a 7. pozícióban van. A 7. pozícióban azonban E bitje 0, tehát az E csomópont lesz az F csomópont bal oldali gyermeke. A szerkezetet most a 13. ábra szemlélteti.

És végül beszúrjuk a G karaktert. Minden számítás után megállapítjuk, hogy az új csomópontot az F csomópont jobb gyermekeként kell elhelyezni, amelynek diff értéke 8-nak felel meg. A végeredmény a 14. ábrán látható.

Eleddig csak egy karakterből álló karakterláncokat illesztettünk be. Mi történne, ha megpróbálnánk AB és BA karakterláncokat beszúrni? Az érdeklődő olvasó ezt a feltevést feladatnak tekintheti. Két tipp: mindkét karakterlánc különbözik a B csomópont 9. pozíciójában; és a végső trie-t a 15. ábra szemlélteti.

Az utolsó ábrát átgondolva a következő kérdést tehetjük fel: Ahhoz, hogy megtaláljuk például a BA karakterláncot, 5 bit összehasonlításra van szükség, míg ennek a karakterláncnak a hash kódjának kiszámításához csak két iterációra van szükség, tehát mikor válik versenyképessé a PATRICIA Trie? Képzeljük el, ha ebbe a struktúrába beillesztjük az ABBABABABBBBABABABBA karakterláncot (az 1968-as PATRICIA eredeti tanulmányának példájából), amely 16 karakter hosszú? Ezt a karakterláncot az AB csomópont bal oldali gyermekeként helyeznénk el a 17. pozícióban lévő diff-vel. Ahhoz, hogy megtaláljuk, 5 bit összehasonlításra lenne szükségünk, míg a hash-kód kiszámításához 16 iterációra lenne szükség, minden karakterre egy, ez az oka annak, hogy a PATRICIA Trie olyan versenyképes hosszú karakterláncok keresésekor.
PATRICIA Trie vs Hash Map
Ez utolsó fejezetben a Hash Mapet és a PATRICIA Trie-t hasonlítom össze két alkalmazásban. Az első egy szószámlálás az 1 millió véletlenszerű mondatot tartalmazó leipzig1m.txt fájlon, a második pedig egy szimbólumtábla feltöltése több mint 2,3 millió URL-címmel az innen letöltött DMOZ projektből (2017-ben bezárt).
A kód, amelyet fejlesztettem és használtam mind a fenti pszeudokód megvalósításához, mind a PATRICIA Trie és a Hash Table teljesítményének összehasonlításához, megtalálható a GitHubomban.
Ezeket az összehasonlításokat az Ubuntu 18.04-es boxomon futtattam. A konfiguráció a 16. ábrán
található.