パーセンタイルとは、分布において「それ以下」(その左側)の分布が指定量(または割合)ある場所のことをいいます。 つまり、#n^”th “# パーセンタイルを#x# とし、分布から乱数#X# を引いたとき、#X# が#x# よりも小さい確率は#n %#:
#n^”th” ” パーセンタイル ” = x” です。 “#means#” ” P(X < x)=n%.#
例えば、標準正規曲線(#mu=0#、#sigma=1#)において、#x=0#となる点(即ち というのは、曲線の面積の 50% は #x=0# より左に位置するからです:

標準正規分布 #Z# は非常によい基準であり、実際に、この曲線のパーセンタイルを調べるために特に設計された値の表があります。 これは #z# テーブルと呼ばれ、次のようなものです:
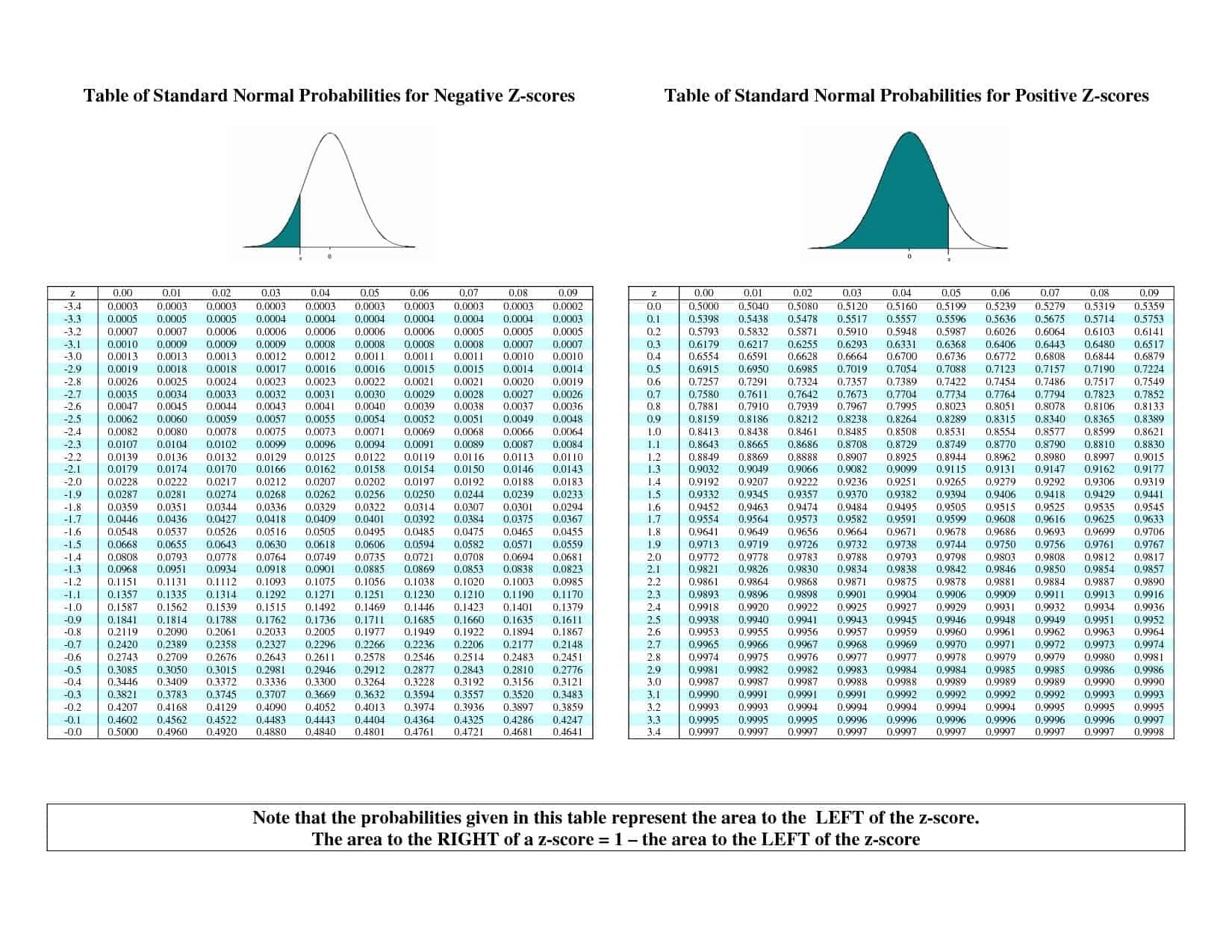
これをどのように使うのでしょうか。 例えば、標準正規分布の25パーセンタイルが欲しいとします。 表の中で0.25に最も近い値(たまたま0.2514でした)を見つけ、それが行#”-“0.6#、列#0.07#にあることを確認します。 この表から、25 パーセンタイルは(およそ) #”-“0.67# ということになります。
でも、どんな正規分布 #X# でも、パーセンタイルが必要なときに、それが役に立つのでしょうか。 私たちは任意の曲線と標準正規曲線の間の接続を見つける必要があります。 その接続は#X#分布を#0#を中心とするように左右にシフトし、その標準偏差が#1#となるように伸縮させることで見つかります。 その公式は次の通りです:
#Z=(X-mu)/sigma#
ここで#mu#は#X#の平均、#sigma#は#X#のs.d.を表しています。
Z#分布から欲しいパーセンタイルが分かっていれば、式を
#X=sigma Z + mu#に直して#X#を解けばよいのです。
例として、最初の質問で、#X#が#mu = 81.2# と#sigma = 12.4# で正規分布し、16パーセンタイルを求める場合を考えてみましょう。
上の表から、#Z#分布の16%は約 #”-“0.99# となります。 このとき、#X#分布における同等の位置は、
#X=(12.4)(“-“0.99)+81.2#
#color(white)X=”-“12.276+81.2##X#分布における同等の位置は、次のようになります。2#
#color(white)X=68.924#
ここで言えることは、#X# が #mu=81.2 ” feet “# で #sigma=12.2 の正規曲線とすると、#X# は 12.4 ” feet “# となります。4 ” feet “# なら、#X# の観測値が #68.924 ” feet “# より小さい確率は 16% です。
残りは練習問題として残しておきます。