1件がカートに追加されました。

ORDER STATA

Markov-switching models

これってどうなんでしょう？

時とともにプロセスが進化し、結果が離散的に変化することがある。

経済の景気後退と景気拡大を考えてみよう。 不況の始まりには、生産と雇用が低下し、低いままであり、その後、生産と雇用は増加する。 双極性障害では、躁の後に鬱の時期があり、それを繰り返すと考える。 統計的には、平均値や分散などのパラメータは、エピソード（レジーム）をまたいで変化しています。 我々の問題は、レジームがいつ変化するか、そして各レジームに関連するパラメータの値を推定することである。 レジームがいつ変化するかを問うことは、レジームがいつまで続くかを問うことと同じである。

マルコフ推移モデルでは、各レジームの平均や分散などを推定するのに加えて、レジームが変化する確率も推定することになる。 ある問題に対して推定された遷移確率は次のようなものであろう。

1 2

0.75 0.25

from/to
state
1		0.82 0.18
2

状態1でスタートする。 状態1から状態1へ遷移する確率は0.82である。 言い換えれば、一度状態1になると、プロセスはそこに留まる傾向がある。 しかし、0.18の確率で、プロセスは状態2に移行する。 状態2はそれほど永続的ではない。 確率0.75で、プロセスは次の時間帯に状態2から状態1へ戻る。

マルコフ切替モデルは、2レジームモデルが一般的であるが、2レジームに限定されるものではない。

上の例では、切り替えが突然で、確率が瞬時に変わると表現した。 このようなマルコフモデルを動的モデル（dynamic model）という。 また、マルコフモデルは、遷移確率を自己回帰過程としてモデル化することで、より滑らかな変化に対応することができます。

このように、切り替えはスムーズにも突然にもなり得るのです。

Let’s see it work

Let’s look at mean changes across regimes. 特に、フェデラルファンド・レートについて分析します。 フェデラルファンドレートとは、米国の中央銀行が商業銀行に対して夜間融資を行う際に課す金利のことです。 ここでは、1954年から2010年末までのフェデラルファンドレートの変化を見ることにする。 以下はそのデータである。

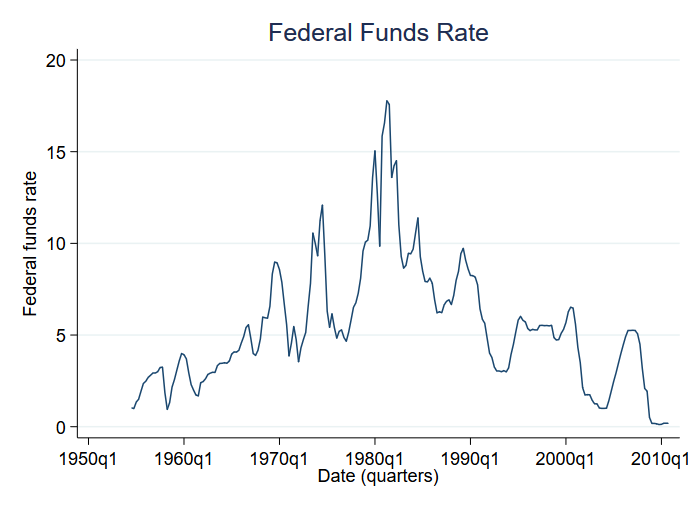
四半期ごとのデータです。 高金利は70年代と80年代を特徴づけているようです。 他の年代を特徴づけるような低金利の体制がもう一つあると仮定する。

2つのレジームを持つdynamic-switching (abrupt-change) モデルをあてはめるには、

. mswitch dr fedfundsPerforming EM optimizaton:Performing gradient-based optimization:

反復0：	log likelihood = -508.66031
反復1:	log likelihood = -508.6382
反復2:	log likelihood = -508.68.63592
反復3:	log likelihood = -508.63592

Markov-switching dynamic regressionサンプル：1954q3 – 2010q4 No. of obs = 226Number of states = 2 AIC = 4,5455無条件確率: transition HQIC = 4,5760 SBIC = 4,6211Log likelihood = -508.63592

9.556793 .2999889 31.86 0.000 8.968826 10.14476

sigma

fedfunds	Coef.Likelihood
State1
_cons	3.70877 .1767083 20.99 0.000 3.362428 4.055112
State2
_cons
	2.107562 .1008692 1.918851 2.107562 .1008692 1.918851 2.107562 .1008692 1.918851 3.107562 .1008692 2.107562 .1008692 3.107582 3.107682.1.107682.1.107582.1.107682.2.107682.1.107682.1.107682.1.107682.1.107682.1.107682.2314831
p11		.9820939 .0104002 .9450805 .9943119
p21		.0503587 .0268434 .0173432 .1374344

上記の出力で報告されるのは、

• 二つの状態の平均 (_cons);
• プロセス全体に対する一つの標準偏差 (sigma); および
• 状態1から1、状態2から1への移行確率 (p11 と p21)、です。

状態1は中レート状態（平均3.71％）である。

State2は高レート状態（平均9.56％）です。

0.05 1 – 0.05

from/to
state		1 2
1		0.98 1 – 0.98
2

いずれの状態も信じられないほど持続します（1->1、2->2確率は0.98および0.95）。

推定後に予測できるものの中に、様々な状態にある確率があります。 状態は2つしかないので、（例えば）状態2にある確率は、両方の状態の確率を教えてくれる。 予測された確率を求め、元のデータとともにグラフ化することができます。

. predict prfed, pr

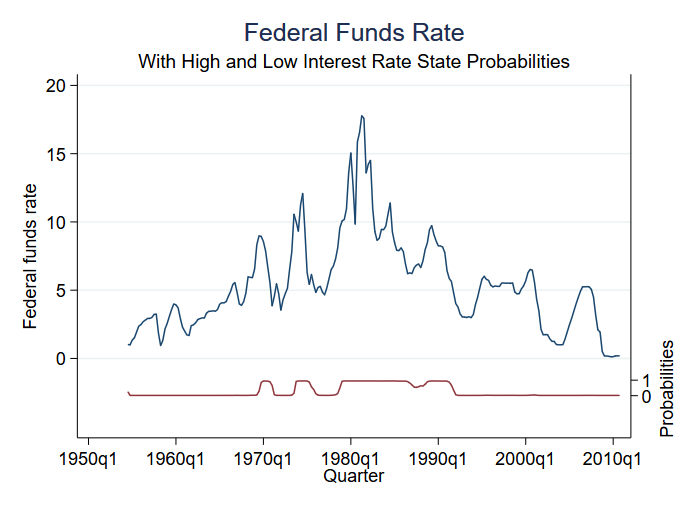
このモデルは、どの時点でもレジームに関してほとんど不確実性がないことがわかります。 高レート状態の期間が3回、中レート状態の期間が4回あることがわかる。

Let’s see it work

疾病発生の例として、1929年から1972年のニューヨーク市における住民1万人当たりのおたふく風邪を見てみましょう。 発生は平均値の変化に対応すると思うかもしれませんが、データで見ることができるのは、さらに大きな分散の変化です。

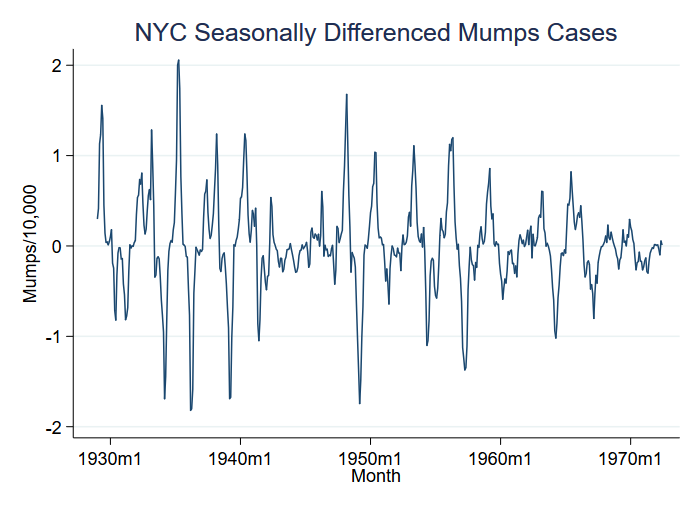
私たちは変数S12.mumpspc、つまり12ヶ月間の一人当たりのおたふくかぜの季節差をグラフ化し、S12.mumpspcを分析しようと思っています。

S12.mumpspcの平均と分散が変化する2つのレジームを想定しています。 動的（abrupt-change）モデルを当てはめるために、

. mswitch dr S12.mumpspc, varswitch switch(LS12.mumpspc, noconstant)Performing EM optimizaton:Performing gradient-based optimization:

反復0：	log尤度 = 110.9372 （非凹）
反復1：	log尤度 = 120.9772 （非凹）とタイプします。68028
反復2:	log尤度 = 123.23244
反復3:	log尤度 = 131.47084
Iteration 3:	log尤度 = 131.23244(尤度は)。72182
Iteration 3:	log likelihood = 131.7225
Iteration 3:	log likelihood = 131.7225

マーコフ・スイッチング動的回帰サンプル： 1929m2 – 1972m6 No. of obs = 521Number of states = 2 AIC = -0.4826Unconditional probabilities: transition HQIC = -0.4634 SBIC = -0.4336Log likelihood = 131.7225

.0562405 .0050954 .0470901 .067169

S12.mumspc	Coef.LIKING
State1
mumpspc
LS12.State1.State2
LS12.State2>
			LS12.State3		.4202751 .0167461 25.10 0.000 .3874533 .4530968
State2
mumpspc
LS12.		.9847369 .0258383 38.11 0.000 .9340947 1.035379
sigma1
sigma2	.2611362 .0111191 .2402278 .2838644
p11		.762733 .0362619 .6846007 .8264175
p12		.1473767 .0257599 .1036675 .205294

Reported are

• S12の2状態の平均値である。mumpspc (0.42 and 0.98);
• 2つの状態の標準偏差 (0.06 and 0.26); and
• state 1 to 1 and state 2 to 1の遷移確率 (0.76 and 0.15).

State 1 is the low-variance state.状態1は低バランスの状態です。

移行確率のフルセットは以下の通りである。