Data Whitening - MultivariateStats 0.1.0 documentation

Data Analysis¶

データセットが与えられると、fitメソッドを使用して白色化変換を推定できる。

fit(Whitening, X; …)¶

Xで与えられたデータから白色化変換を推定する。ここで、Xは行列であり、その列はサンプルを与える。

この関数はWhiteningのインスタンスを返す。

キーワード引数:

name description default

regcoef

name	description	default
regcoef	正規化係数を指定します。共分散は`regcoef`が正のとき次のように正則化される: `C + (eigmax(C) * regcoef) * eye(d)`	`zero(T)`
mean	mean vector, which can be either: `0`のいずれかとなる: 5195> `nothing`: この関数は平均を計算する計算済みの平均ベクトル	`nothing`

正規化係数を指定します。共分散はregcoefが正のとき次のように正則化される:

C + (eigmax(C) * regcoef) * eye(d)

zero(T)

mean

mean vector, which can be either:

nothing

Note: この関数は変換 W を導くために内部的に cov_whiten に依存している。関数cov_whiten自体も有用な関数である。

cov_whitening(C)¶

共分散行列Cを与えて、白色化変換係数行列Wを導出する。ここでCは正方行列かCholeskyのインスタンスである。

内部的にはこの関数はコレスキー分解を用いて白色化変換を解くものである。その根拠は、C} = \mathbf{U}^T \mathbf{U}, 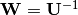$Mathbf{W} = \mathbf{U}^{-1}$ とすると、W}^T \mathbf{C}Mathbf{W}

注：戻り行列Wは上三角行列です。

cov_whitening(C, regcoef)

正規化共分散に基づいて、C + (eigmax(C) * regcoef) * eye(d)としてホワイトニング変換を導出します。

さらに、入力行列Cを計算中に上書きするcov_whiten!も用意されています。

invsqrtm(C)¶

対称固有値分解によりinv(sqrtm(C))を計算する。