上の最初のプロットは、大きなバッチサイズがエポックあたりの移動距離を少なくしていることを示しています。 バッチ32の学習エポック距離は0.15から0.4まで変化し、バッチ256の学習では0.02から0.04程度になります。 実際、2番目のプロットでわかるように、エポック距離の比率は時間とともに増加します!
しかし、なぜ大きなバッチ学習はエポックあたりの距離を少なくトラバースするのでしょうか? それは、バッチ数が少なく、したがってエポックあたりの更新回数が少ないからでしょうか。 それとも、各バッチの更新がより少ない距離を通過するからでしょうか?
この質問に答えるために、各バッチ更新のサイズを測定してみましょう。

Median batch update norm for batch size 32: 3.3e-3
Median batch update norm for batch size 256: 1.5e-3
バッチサイズが大きくなると各バッチ更新が小さくなることがわかるでしょう。 なぜそうなるのでしょうか。
この動作を理解するために、2つの勾配ベクトルa、bがあり、それぞれが1つの学習例に対する勾配を表しているというダミーシナリオを設定しましょう。 バッチサイズ=1の場合の平均バッチ更新サイズと、バッチサイズ=2の場合の平均バッチ更新サイズを比較して考えてみましょう。

バッチサイズ1で行うと、a、bと一通り進んでa+bで表される点に行きつくことになる。 (厳密には、bの勾配はaを適用した後に再計算されますが、今は無視しましょう)。 この結果、平均バッチ更新サイズは (|a|+|b|)/2 – バッチ更新サイズの合計をバッチ更新数で割ったもの – になります。
しかしながら、バッチサイズを 2 とすると、バッチ更新は代わりにベクトル (a+b)/2 – 図 12 の赤矢印 – で表されます。 したがって、平均バッチ更新サイズは|(a+b)/2| / 1 =|a+b|/2.
では、2つの平均バッチ更新サイズを比較してみましょう:

最後の行では、三角形の不等式を使って、バッチサイズ1の平均バッチ更新サイズは常にバッチサイズ2のそれ以上であることを示しました。
別の言い方をすると、バッチサイズ1とバッチサイズ2の平均バッチサイズが等しいためには、|a|+|b|=|a+b|のときなのでベクトルaとbが同じ方向を向いていなければならないのです。 この議論をn個のベクトルに拡張することができます – すべてのn個のベクトルが同じ方向を向いているときだけ、バッチサイズ=1とバッチサイズ=nの平均バッチ更新サイズは同じになります。 しかし、勾配ベクトルが全く同じ方向を向いていることはまずないので、これはほとんどありえません。

Figure 16のミニバッチ更新式に戻ると、ある意味でバッチサイズ|B_k|をスケールアップすると、勾配の和の大きさが比較的早くスケールアップしないことを言っていることになる。 これは、勾配ベクトルが異なる方向を向いているため、バッチサイズ(すなわち、合計する勾配ベクトルの数)を2倍にしても、結果として得られる勾配ベクトルの合計の大きさが2倍にならないためである。 同時に、2 倍大きい分母 |B_k| で割っているため、全体的に小さな更新ステップになります。
これは、より大きなバッチ サイズのバッチ更新が小さくなる傾向がある理由を説明できます。
Hypothesis 2: Small batch training finds flatter minimizers
ここで、両方の最小化器のシャープネスを測定し、小さいバッチ トレーニングがよりフラットな最小化器を見つけるという主張を評価しましょう。 (この2つ目の仮説は1つ目の仮説と共存可能であり、相互に排他的ではないことに注意されたい)。 そのために、Keskarらから2つの方法を借りる。
最初の方法では、小バッチ最小化器(バッチサイズ32)と大バッチ最小化器(バッチサイズ256)の間の線に沿って学習と検証のロスをプロットする。 この線は次の式で記述される:

よりここで、x_l*は大バッチ最小化器、x_s*は小バッチ最小化器、αは-1から2までの係数。

プロットでわかるように、小バッチ最小化器(α=0)は大バッチ最小化器(α=1)よりはるかに平坦で、よりシャープに変化する。
これは1方向のみを考慮するので、シャープさを測定するかなり単純な方法であることに注意してください。 そこで、Keskarらは、損失関数が最小化器の周りの近傍でどれだけ変化するかを測定するシャープネス指標を提案する。 まず、近傍を次のように定義する:

よりここでεは近傍の大きさを定義するパラメータで、xは最小化因子(重み)である。
そして、最小化器の周りのこの近傍における最大損失としてシャープネス指標を定義する:

よりここでfは損失関数で、入力は重みである。
上記の定義で、イプシロン値を1e-3として、様々なバッチサイズでの最小化器のシャープネスを計算してみよう:
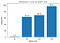
これは、補間プロットで見たように、大きなバッチの最小化器が確かにシャープであることを示します。
最後に、Li らによって定式化されたフィルタ正規化損失の視覚化で最小化器をプロットしてみましょう。 このタイプのプロットは、モデル重みと同じ次元で2つのランダムな方向を選び、そして、各畳み込みフィルター(またはFC層の場合はニューロン)を、モデル重みの対応するフィルターと同じノルムを持つように正規化します。 これにより、最小化器のシャープさがその重みの大きさに影響されないようにする。 そして、この2つの方向に沿って損失をプロットし、プロットの中心を特徴づけたい最小化因子とする
。