W mikrokosmosie, w którym jestem osadzony, struktury danych typu trie nie są zbyt popularne. Środowisko to składa się głównie z data scientists oraz, w mniejszej liczbie, inżynierów oprogramowania, zajmujących się przetwarzaniem języka naturalnego (NLP).
Ostatnio trafiłem na ciekawą dyskusję na temat tego, kiedy używać trie czy hash table. Chociaż nie było nic nowego w tej dyskusji, którą mogę tutaj zgłosić, jak plusy i minusy każdej z tych dwóch struktur danych (jeśli wygooglujesz trochę, znajdziesz wiele linków odnoszących się do nich), to co było dla mnie nowe, to specjalny typ trie zwany Patricia Trie i to, że w niektórych scenariuszach ta struktura danych wykonuje porównywalnie zarówno w czasie przetwarzania, jak i przestrzeni z tablicą haszującą, jednocześnie adresując zadania, takie jak listowanie ciągów ze wspólnym prefiksem bez dodatkowych kosztów.
Mając to na uwadze, szukałem jakiegoś artykułu lub bloga, który pomógłby mi zrozumieć w prosty sposób (eufemizm dla lenistwa) jak działa algorytm PATRICIA, specjalnie służąc jako skrót do przeczytania 21-stronicowej pracy opublikowanej w 1968 roku. Niestety nie odniosłem sukcesu w tych poszukiwaniach, nie pozostawiając sobie żadnej alternatywy dla jej przeczytania.
Moim celem w tej historii jest wypełnienie powyższej luki, tj. posiadanie historii opisującej w kategoriach laika algorytm, o którym mowa.
Aby osiągnąć mój cel, najpierw, krótko i zwięźle, przedstawię, dla tych, którzy nie znają prób, tę strukturę danych. Po tym wprowadzeniu, wymienię najpopularniejsze trie, które pozwolą mi zaimplementować i szczegółowo opisać jak działa PATRICIA Trie i dlaczego działa tak dobrze. Zakończę tę historię porównując wyniki (wydajność i zużycie miejsca) w dwóch różnych aplikacjach: pierwsza to liczenie słów (<WORD, FREQUENCY> tuples) na podstawie dość dużego tekstu; a druga to budowanie <URL, IP> tuples, na podstawie listy ponad 2 milionów adresów URL, która jest podstawowym elementem serwera DNS. Obie aplikacje zostały zbudowane w oparciu o Hash Map i Patricia Trie.
Jak definiują Sedgewick i Wayne z Princeton University w swojej książce Algorithms – Fourth Edition (wydawca: Addison-Wesley) trie, lub drzewo prefiksowe, jest „strukturą danych zbudowaną ze znaków klucza wyszukiwania w celu prowadzenia wyszukiwania”. Ta „struktura danych składa się z węzłów, które zawierają linki, które są albo zerowe, albo odnoszą się do innych węzłów. Każdy węzeł jest wskazywany przez tylko jeden inny węzeł, który jest nazywany jego rodzicem (z wyjątkiem jednego węzła, korzenia, który nie ma węzłów wskazujących na niego), a każdy węzeł ma S linków, gdzie S to rozmiar alfabetu (lub zestaw znaków)”.
Rysunek 1 poniżej, zgodnie z powyższą definicją, zawiera przykład trie.

Węzeł root nie ma etykiety. Ma on troje dzieci: węzły o kluczach „a”, „h” i „s”. W prawym dolnym rogu rysunku znajduje się tabela, w której wypisane są wszystkie klucze wraz z odpowiadającymi im wartościami. Od korzenia możemy przejść do 'a’ -> 'i’ -> 'r’. Sekwencja ta tworzy słowo „air” o wartości (np. ilość wystąpień tego słowa w tekście) 4 (wartości znajdują się wewnątrz zielonej ramki). Zgodnie z konwencją istniejące słowo w tabeli symboli ma wartość nie zerową. Tak więc, chociaż słowo „airway” istnieje w języku angielskim, nie ma go w tym trie, ponieważ zgodnie z konwencją wartość węzła z kluczem „y” jest null.
Słowo „air” jest również prefiksem dla słów: „airplane”; oraz „airways”. Sekwencja 'h’ -> 'a’ tworzy przedrostek „has” i „hat”, podobnie jak sekwencja 'h’ -> 'o’ tworzy przedrostek „house” i „horse”.
Oprócz tego, że dobrze służy jako struktura danych dla, powiedzmy, słownika, służy również jako ważny element aplikacji do uzupełniania. System mógłby zaproponować słowa „airplane” i „airways” po wpisaniu przez użytkownika słowa „air”, przemierzając poddrzewo, którego korzeniem jest węzeł z kluczem „r”. Dodatkową zaletą tej struktury jest to, że możesz uzyskać uporządkowaną listę istniejących kluczy, bez dodatkowych kosztów, poprzez przeglądanie trie w orientacji in-order, układając dzieci węzła i przeglądając je od lewej do prawej.
Na rysunku 2 przedstawiono przykład anatomii węzła.

Interesującym elementem tej anatomii jest to, że wskaźniki do dzieci są zwykle przechowywane w tablicy. Jeśli reprezentujemy zestaw znaków S, na przykład Extended ASCII, potrzebujemy tablicy o rozmiarze 256. Mając dziecko znaku możemy uzyskać dostęp do jego wskaźnika w rodzicu w czasie O(1). Biorąc pod uwagę, że rozmiar słownika wynosi N, a rozmiar najdłuższego słowa wynosi M, głębokość trie wynosi również M i przejście przez strukturę zajmuje O(MN) czasu. Jeśli weźmiemy pod uwagę, że zwykle N jest znacznie większe niż M (liczba słów w korpusie jest znacznie większa niż rozmiar najdłuższego słowa), możemy uznać, że O(MN) jest liniowe. W praktyce tablica ta jest nieliczna, tzn. większość węzłów ma znacznie mniej dzieci niż S. Dodatkowo, średni rozmiar słów jest również mniejszy niż M, a więc w praktyce, średnio, wyszukiwanie klucza zajmuje O(logₛ N), a przemierzanie całej struktury O(N logₛ N).
Istnieją dwa główne problemy związane z tą strukturą danych. Jednym z nich jest zużycie miejsca. Na każdym poziomie L, zaczynając od zera, znajduje się asymptotycznie Sᴸ wskaźników. O ile w przypadku Extended ASCII, czyli 256 znaków jest to problem w ograniczonych urządzeniach pamięciowych, to sytuacja pogarsza się, gdy weźmiemy pod uwagę wszystkie znaki Unicode (jest ich 65.000). Drugim problemem jest ilość węzłów z jednym dzieckiem, co pogarsza wydajność wprowadzania i wyszukiwania danych. W przykładzie na rysunku 1 tylko korzeń, klucz „h” na poziomie 1, klucze „a” i „o” na poziomie 2 oraz klucz „r” na poziomie 3 mają więcej niż jedno dziecko. Innymi słowy, tylko 5 węzłów z 27 ma dwoje lub więcej dzieci. Alternatywy dla tej struktury rozwiązują głównie te problemy.
Przed opisaniem alternatywy (PATRICIA Trie), odpowiem na następujące pytanie: dlaczego alternatywy, jeśli możemy użyć tablicy hash zamiast tablicy? Hash table rzeczywiście pomaga zaoszczędzić pamięć przy niewielkim spadku wydajności, ale nie rozwiązuje problemu. Im wyżej jesteś w trie (bliżej poziomu zero), tym bardziej prawdopodobne jest, że prawie wszystkie znaki w dowolnym zestawie znaków będą musiały być zaadresowane. Dobrze zaimplementowane tablice haszujące, takie jak ta w Javie (zdecydowanie wśród najlepszych, prawdopodobnie najlepsza), zaczynają się od domyślnego rozmiaru i automatycznie zmieniają rozmiar zgodnie z progiem. W Javie domyślny rozmiar to 16 z progiem 0,75 i podwaja swój rozmiar w każdej z tych operacji. Biorąc pod uwagę Extended ASCII, do czasu, gdy liczba dzieci w jednym węźle osiągnie 192, tablica hash będzie miała rozmiar 512, mimo że potrzebuje tylko 256 na końcu.
Radix Trie
Jako że PATRICIA Trie jest specjalnym przypadkiem Radix Trie, zacznę od tego ostatniego. W Wikipedii Radix Trie jest zdefiniowany jako „struktura danych, która reprezentuje zoptymalizowany przestrzennie trie… w którym każdy węzeł, który jest jedynym dzieckiem jest łączony ze swoim rodzicem… W przeciwieństwie do zwykłych drzew (gdzie całe klucze są porównywane masowo od ich początku aż do punktu nierówności), klucz w każdym węźle jest porównywany kawałek po kawałku, gdzie ilość bitów w tym kawałku w tym węźle jest radixem r radix trie”. Definicja ta będzie miała więcej sensu, gdy zilustrujemy ten trie na rysunku 3.
Liczba dzieci r węzła w trie radix jest określona następującym wzorem, gdzie x jest liczbą bitów potrzebnych do porównania powyższego chunk-of-bits:

Powyższy wzór określa liczbę dzieci w trie radix jako zawsze wielokrotność 2. Na przykład dla 4-Radix Trie, x = 2. Oznacza to, że musielibyśmy porównywać kawałki dwóch bitów, parę bitów, ponieważ za pomocą tych dwóch bitów reprezentujemy wszystkie liczby dziesiętne od 0 do 3, w sumie 4 różne liczby, po jednej dla każdego dziecka.
Aby lepiej zrozumieć powyższe definicje, rozważmy przykład z rysunku 3. W tym przykładzie mamy hipotetyczny zestaw znaków składający się z 5 znaków (NULL, A, B, C i D). Wybrałem, aby reprezentować je przy użyciu tylko 4 bitów (pamiętaj, że nie ma to nic wspólnego z r, trzeba tylko 3 bity do reprezentowania 5 znaków, ale ma do czynienia z łatwością rysowania przykładu). W lewym górnym rogu rysunku znajduje się tabela mapująca każdy znak do jego reprezentacji bitowej.
Aby wstawić znak 'A’, porównam go bitowo z NULL. W prawym górnym rogu rysunku 3, w polu oznaczonym cyfrą 1 w żółtym rombie, możemy zobaczyć, że te dwa znaki różnią się w pierwszej parze. Ta pierwsza para jest reprezentowana na czerwono w 4-bitowej reprezentacji A. Tak więc DIFF zawiera pozycję bitową, gdzie kończy się inna para.
Aby wstawić znak 'B’ musimy porównać go bitowo ze znakiem 'A’. Porównanie to znajduje się w rombowym polu oznaczonym 2. Różnica przypada tym razem na drugą parę bitów, w kolorze czerwonym, która kończy się na pozycji 4. Ponieważ druga para to 01 tworzymy węzeł z kluczem B i kierujemy do niego adres 01 z węzła A. To powiązanie widać w dolnej części rysunku 3. Ta sama procedura dotyczy wstawiania znaków 'C’ i 'D’.

W powyższym przykładzie widzimy, że pierwsza para (01 na niebiesko) jest prefiksem wszystkich wstawianych znaków.
Przykład ten służy do opisania porównywania kawałków bitów, optymalizacji przestrzeni (tylko cztery dzieci w tym przypadku, niezależnie od wielkości zestawu znaków) i łączenia rodzic/dziecko (w węzłach dzieci przechowywane są tylko te bity, które różnią się od korzenia), o których mowa w powyższej definicji drzewa radix. Mimo to, nadal istnieje jeden link wskazujący na węzeł zerowy. Sparseness jest wprost proporcjonalna do r i głębokości trie.
PATRICIA Trie
PATRICIA (Practical Algorithm to Retrieve Information Coded in Alphanumeric, Journal of the ACM, 15(4):514-534, October 1968) . Tak, PATRICIA jest akronimem!
PATRICIA Trie jest tu zdefiniowane przez trzy reguły:
- Każdy węzeł (TWIN jest oryginalnym terminem PATRICIA) ma dwoje dzieci (r = 2 i x = 1 w terminach Radix Trie);
- Węzeł jest podzielony na prefiks (L-PHRASE w terminach PATRICIA) z dwojgiem dzieci (każde dziecko tworzy BRANCH, który jest oryginalnym terminem PATRICIA) tylko wtedy, gdy dwa słowa (PROPER OCCURRENCE w terminach PATRICIA) dzielą ten sam prefiks; oraz
- Każde słowo kończące się będzie reprezentowane wartością wewnątrz węzła różną od null (znak END w oryginalnej nomenklaturze PATRYCJI)
Zasada numer 2 powyżej powoduje, że długość prefiksu na każdym poziomie jest większa od długości prefiksu z poprzedniego poziomu. Będzie to bardzo ważne w algorytmach obsługujących operacje PATRICIA, takie jak wstawianie elementu lub znajdowanie innego elementu.
Z powyższych reguł można zdefiniować węzeł w sposób przedstawiony poniżej. Każdy węzeł ma jednego rodzica, z wyjątkiem korzenia, oraz dwoje dzieci, wartość (dowolnego typu) i zmienną diff wskazującą pozycję podziału w kodzie bitowym klucza

Aby użyć algorytmu PATRICIA potrzebujemy funkcji, która dając 2 ciągi znaków zwróci pozycję pierwszego bitu, od lewej do prawej, na której się różnią. Widzieliśmy już jak to działa dla Radix Trie.
Aby obsługiwać trie przy użyciu PATRICIA, tzn. wstawiać lub znajdować w nim klucze, potrzebujemy 2 wskaźników. Jeden z nich to parent, zainicjalizowany przez wskazanie na węzeł główny. Drugi to child, inicjalizowany przez wskazanie na lewe dziecko korzenia.
W dalszej części instrukcji zmienna diff będzie przechowywała pozycję, w której wstawiany klucz różni się od child.key. Zgodnie z regułą numer 2 definiujemy następujące 2 nierówności:


Let found wskazuje na węzeł, w którym kończy się poszukiwanie klucza. Jeśli found.key jest różny od wstawianego łańcucha, diff zostanie obliczony, za pomocą funkcji ComputeDiff, przy użyciu tego łańcucha i found.key. Jeżeli są one równe, to klucz istnieje w strukturze i, jak w każdej tablicy symboli, powinna zostać zwrócona wartość. Podczas operacji będzie używana metoda pomocnicza o nazwie BitAtPosition, która pobiera bit na określonej pozycji (0 lub 1).
Aby wyszukiwać musimy zdefiniować funkcję Search(key). Jej pseudokod znajduje się na rysunku 4.

Drugą funkcją, którą wykorzystamy w tej historii jest Insert(klucz). Jej pseudokod znajduje się na rysunku 6.

W powyższym pseudokodzie znajduje się metoda do tworzenia węzła o nazwie CreateNode. Jej argumenty można zrozumieć z rysunku 4.
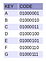
Aby zilustrować działanie PATRICIA Trie, wolę poprowadzić czytelnika krok po kroku przez operację wstawiania 7 znaków (’A’, 'B’, 'C’, 'D’, 'E’, 'F’ i 'G’, jak podano na rysunku 7 obok) w ich naturalnej kolejności. Na koniec, miejmy nadzieję, zrozumiemy, jak działa ta struktura danych.
Znak A jest wstawiany jako pierwszy. Jego kod bitowy to 01000001. Podobnie jak w Radix Trie, porównamy ten bitkod z kodem w korzeniu, który w tym momencie jest zerowy, a więc porównamy 000000 z 01000001. Różnica wypada na pozycji 2 (tutaj jako x = 1 porównujemy bit po bicie, a nie ich parę).

Aby utworzyć węzeł musimy wskazać lewe i prawe dziecko na ich odpowiednie następniki. Ponieważ ten węzeł jest korzeniem, z definicji jego lewe dziecko wskazuje na siebie, podczas gdy jego prawe dziecko wskazuje na null. Będzie to jedyny wskaźnik null w całym trie. Pamiętajmy, że korzeń jest jedynym węzłem, który nie ma rodzica. Wartość, w naszym przykładzie będą to liczby całkowite naśladujące aplikację liczącą słowa, jest ustawiona na 1. Wynik tej operacji wstawiania jest pokazany na rysunku 8.
Następnie wstawimy znak B o kodzie bitowym 01000010. Pierwszą rzeczą jest sprawdzenie, czy znak ten znajduje się już w strukturze. W tym celu wyszukujemy go. Wyszukiwanie w triadzie PATRICIA jest proste (patrz pseudokod na rysunku 5). Po porównaniu klucza korzenia z kluczem B dochodzimy do wniosku, że są one różne, więc tworzymy dwa wskaźniki: parent i child. Początkowo parent wskazuje na korzenia, a child na lewe dziecko korzenia. W tym przypadku oba wskazują na węzeł A. Zgodnie z zasadą numer 2, będziemy iterować strukturę, podczas gdy nierówność (1) jest prawdziwa.
W tej chwili parent.DIFF jest równe, i nie mniejsze niż, child.DIFF. To łamie nierówność (1). Ponieważ child.VALUE jest różne od null (równe 1) porównujemy znaki. Ponieważ A jest różne od B, oznacza to, że B nie znajduje się w trie i musi zostać wstawione.
Aby wstawić zaczynamy, ponownie, definiując rodzica i dziecko tak jak poprzednio, tzn. rodzic wskazuje na korzeń, a dziecko wskazuje na jego lewy węzeł. Iteracja przez strukturę musi być zgodna z nierównościami (1) i (2). Kontynuujemy obliczając diff, który jest różnicą, bitową, pomiędzy B i child.KEY, który na tym etapie jest równy A (różnica pomiędzy bitkodami 01000001 i 01000010) . Różnica przypada na bit na pozycji 7 , więc diff = 7.

W tym momencie parent i child wskazują na ten sam węzeł (na węzeł A, czyli root). Ponieważ nierówność (1) jest już fałszywa, a child.DIFF jest mniejsze niż diff, utworzymy węzeł B i wskażemy na niego parent.LEFT. Podobnie jak to zrobiliśmy z węzłem A, musimy wskazać gdzieś dzieci węzła B. Bit na pozycji 7 w B wynosi 1, więc prawe dziecko węzła B będzie wskazywało na siebie. Lewe dziecko węzła B będzie wskazywało na rodzica, czyli w tym przypadku na korzeń. Wynik końcowy pokazany jest na rysunku 9.
Poprzez wskazanie lewego dziecka węzła B na jego rodzica umożliwiamy podział, o którym mowa w regule numer 2. Gdy wstawimy znak, którego diff mieści się w przedziale od 2 do 7, wskaźnik ten odeśle nas z powrotem do właściwej pozycji, z której wstawiamy nowy znak. Tak się stanie, gdy wstawimy znak D.
Wcześniej jednak musimy wstawić znak C o kodzie bitowym równym 01000011. Pointer parent będzie wskazywał na węzeł A (korzeń). Tym razem, inaczej niż podczas szukania znaku B, dziecko wskazuje na węzeł B (wtedy oba wskaźniki wskazywały na korzeń).
W tym momencie zachodzi nierówność (1) (parent.DIFF jest mniejsze niż child.DIFF), więc aktualizujemy oba wskaźniki, ustawiając parent na child, a child na prawe dziecko węzła B, ponieważ na pozycji 7 bit C ma wartość 1.
Po aktualizacji oba wskaźniki wskazują na węzeł B, łamiąc nierówność (1). Podobnie jak poprzednio, porównujemy bitcode child.KEY z bitcode C (01000010 z 01000011) dochodząc do wniosku, że różnią się one na pozycji 8. Ponieważ na pozycji 7 bit C wynosi 1, nowy węzeł (węzeł C) będzie prawym dzieckiem B. Na pozycji 8 bit C wynosi 1, co sprawia, że ustawiamy prawe dziecko węzła C na siebie, podczas gdy jego lewe dziecko wskazuje na rodzica, węzeł B w tym momencie. Powstała w ten sposób trie znajduje się na rysunku 10.

Następnym znakiem jest D (kod bitu 01000100). Podobnie jak w przypadku wstawiania znaku C, ustawimy początkowo wskaźnik parent na węzeł A, a wskaźnik child na węzeł B. Równanie (1) jest poprawne, więc aktualizujemy wskaźniki. Teraz rodzic wskazuje na węzeł B, a dziecko na lewe dziecko węzła B, ponieważ na pozycji 7 bit D ma wartość 0. Inaczej niż w przypadku wstawiania znaku C, teraz dziecko wskazuje z powrotem na węzeł A, łamiąc nierówność (1). Ponownie obliczamy różnicę pomiędzy bitkodami A i D. Teraz diff wynosi 6. Teraz diff wynosi 6. Ponownie ustawiamy rodzica i dziecko tak jak to robimy normalnie. Teraz, podczas gdy nierówność (1) jest poprawna, nierówność (2) nie jest. Oznacza to, że wstawimy D jako lewe dziecko A. Ale co z dziećmi D? Na pozycji 6 bit D wynosi 1, więc jego prawe dziecko wskazuje na siebie. Interesujące jest to, że lewe dziecko węzła D będzie teraz wskazywać na węzeł B, tworząc trie narysowane na rysunku 11.

Następny jest znak E z kodem bitowym 01000101. Funkcja Szukaj zwróci węzeł D. Różnica między znakami D i E przypada na bit na pozycji 8. Ponieważ na pozycji 6 bit E wynosi 1, zostanie on umieszczony na prawo od D. Strukturę trie przedstawia rysunek 12.

Interesującą rzeczą przy wstawianiu znaku F jest to, że jego miejsce jest między znakami D i E, ponieważ różnica między D i F jest na pozycji 7. Ale na pozycji 7 bit E ma wartość 0, więc węzeł E będzie lewym dzieckiem węzła F. Struktura ta jest teraz przedstawiona na rysunku 13.

And, at last, we insert character G. After all computations we conclude that the new node should be placed as the right child of node F with diff equals to 8. Ostateczny wynik znajduje się na rysunku 14.

Do tej pory wstawialiśmy ciągi składające się tylko z jednego znaku. Co by się stało, gdybyśmy spróbowali wstawić ciągi AB i BA? Zainteresowany czytelnik może potraktować tę propozycję jako ćwiczenie. Dwie podpowiedzi: oba ciągi różnią się od węzła B na pozycji 9; a końcowy trie jest zilustrowany na rysunku 15.

Zastanawiając się nad ostatnim rysunkiem, można zadać następujące pytanie: Aby znaleźć np. ciąg BA potrzebujemy 5 bitowych porównań, natomiast aby obliczyć kod haszujący tego ciągu potrzebujemy tylko dwóch iteracji, więc kiedy PATRICIA Trie staje się konkurencyjna? Wyobraźmy sobie, że wstawimy do tej struktury ciąg ABBABABABBABABBA (zaczerpnięty z przykładu w oryginalnej pracy PATRICIA z 1968 roku), który ma 16 znaków? Ciąg ten zostałby umieszczony jako lewe dziecko węzła AB z diff na pozycji 17. Aby go znaleźć, potrzebowalibyśmy 5 porównań bitowych, podczas gdy obliczenie kodu haszującego zajęłoby 16 iteracji, po jednej dla każdego znaku, co jest powodem, dla którego PATRICIA Trie są tak konkurencyjne przy wyszukiwaniu długich łańcuchów.
PATRICIA Trie vs Hash Map
W tej ostatniej sekcji porównam Hash Map i PATRICIA Trie w dwóch zastosowaniach. Pierwszym z nich jest liczenie słów w pliku leipzig1m.txt zawierającym 1 milion losowych zdań, a drugim jest zapełnienie tabeli symboli ponad 2,3 milionami adresów URL z projektu DMOZ (zamkniętego w 2017 roku) pobranego stąd.
Kod, który opracowałem i wykorzystałem zarówno do zaimplementowania powyższego pseudokodu, jak i porównania wydajności PATRICIA Trie z Hash Table, można znaleźć na moim GitHubie.
Porównania te zostały przeprowadzone w moim Ubuntu 18.04. Konfigurację można znaleźć na rysunku 16
.