No microcosmos em que estou inserido, o gosto da estrutura de dados trie não é tão popular. Este ambiente é composto principalmente por cientistas de dados e, em menor número, engenheiros de software, trabalhando com Natural Language Processing (NLP).
Recentemente eu me encontrei em uma discussão interessante sobre quando usar trie ou tabela de hash. Embora não houvesse nada de novo nessa discussão que eu possa relatar aqui, como os prós e contras de cada uma dessas duas estruturas de dados (se você pesquisar um pouco no Google você encontrará muitos links abordando-as), o que era novo para mim era um tipo especial de trie chamado Patricia Trie e, que em alguns cenários, essa estrutura de dados tem um desempenho comparável tanto em tempo de processamento quanto em espaço com a tabela de hash, enquanto aborda tarefas como listar strings com prefixo comum, sem custo extra.
Com isto em mente, procurei por uma história ou blog para me ajudar a entender de uma forma simples (eufemismo para preguiça) como o algoritmo PATRICIA funciona, servindo especialmente como atalho para a leitura do artigo de 21 páginas publicado em 1968. Infelizmente não tive sucesso nesta busca, não me deixando alternativa para lê-lo.
O meu objetivo com esta história é preencher a lacuna acima, ou seja, ter uma história descrevendo em termos leigos o algoritmo em mãos.
Para atingir meu objetivo, primeiro, e brevemente, vou apresentar, para aqueles não familiarizados com tentativas, esta estrutura de dados. Após esta introdução, vou listar a trilogia mais popular por aí, permitindo-me implementar e descrever em detalhe como o PATRICIA Trie funciona e porque é que eles têm um desempenho tão bom. Vou terminar esta história comparando os resultados (desempenho e consumo de espaço) em duas aplicações diferentes: a primeira é uma contagem de palavras (<WORD, FREQUENCY> tuples) baseada em um texto bastante grande; e a segunda é construir um <URL, IP> tuples, baseado em uma lista de mais de 2 milhões de URLs, que consiste no elemento central de um servidor DNS. Ambas as aplicações foram construídas com base no Hash Map e Patricia Trie.
Como definido por Sedgewick e Wayne da Universidade de Princeton em seu livro Algorithms – Fourth Edition (editora: Addison-Wesley) uma trie, ou árvore de prefixos, é “uma estrutura de dados construída a partir dos caracteres da chave de pesquisa para guiar a pesquisa”. Esta “estrutura de dados é composta de nós que contém links que são nulos ou referência a outros nós”. Cada nó é apontado por apenas um outro nó, que é chamado seu pai (exceto por um nó, a raiz, que não tem nós apontando para ele), e cada nó tem links S, onde S é o tamanho do alfabeto (ou charset)”.
Figure 1 bellow, seguindo a definição acima, contém um exemplo de um trie.

O nó raiz não tem etiqueta. Tem três filhos: nós com as teclas ‘a’, ‘h,’ e ‘s’. No canto inferior direito da figura há uma tabela listando todas as chaves com seus respectivos valores. A partir da raiz podemos atravessar para ‘a’ -> ‘i’ -> ‘r’. Esta sequência forma a palavra “ar” com valor (por exemplo, o número de vezes que esta palavra aparece num texto) de 4 (os valores estão dentro de uma caixa verde). Por convenção, uma palavra existente em uma tabela de símbolos tem um valor não nulo. Então, enquanto a palavra “airway” existe em inglês, ela não está nesta triagem, porque, seguindo a convenção, o valor do nó com a tecla “y” é nulo.
A palavra “air” é também o prefixo para as palavras: “avião”; e “vias respiratórias”. A seqüência ‘h’ -> ‘a’ forma o prefixo de “has” e “hat” como a seqüência ‘h’ -> ‘o’ forma o prefixo de “house” e “horse”.
Besides servindo bem como uma estrutura de dados para, digamos, um dicionário, também serve como um elemento importante de uma aplicação de preenchimento. Um sistema poderia propor as palavras “airplane” e “airways” depois de um usuário ter digitado a palavra “air”, atravessando a sub-árvore cuja raiz é o nó com a chave “r”. Um benefício adicional desta estrutura é que você pode obter uma lista ordenada das chaves existentes, sem custo adicional, ao atravessar a triagem em uma orientação por ordem, empilhando os filhos de um nó e percorrendo-os da esquerda para a direita.
Na figura 2 é exemplificada a anatomia do nó.

A parte interessante nesta anatomia é que os ponteiros das crianças são normalmente armazenados em um array. Se estamos representando um conjunto de caracteres S de, por exemplo, Extended ASCII, precisamos que o array seja de tamanho 256. Tendo um caractere de criança podemos acessar seu ponteiro em seu pai no tempo O(1). Considerando que o tamanho do vocabulário é N e que o tamanho da palavra mais longa é M, a profundidade da trie também é M e é preciso O(MN) para atravessar a estrutura. Se considerarmos que normalmente N é muito maior que M (o número de palavras em um corpus é muito maior que o tamanho da palavra mais longa), podemos considerar O(MN) como sendo linear. Na prática esse array é esparso, ou seja, a maioria dos nós tem muito menos filhos que S. Além disso, o tamanho médio das palavras também é menor que M, assim, na prática, em média, é preciso O(logₛ N) para procurar uma chave e O(N logₛ N) para atravessar toda a estrutura.
Existem duas questões principais com essa estrutura de dados. Um é o consumo de espaço. Em cada nível L, começando com zero, há, assimptoticamente, Sᴸ apontadores. Se com ASCII Estendido, ou seja, 256 caracteres isto é um problema em dispositivos de memória limitada, a situação piora se considerarmos todos os caracteres Unicode (65.000 deles). O segundo é a quantidade de nós com apenas um filho, degradando a entrada e o desempenho da busca. No exemplo da figura 1 apenas a raiz, a tecla ‘h’ no nível 1, as teclas ‘a’ e ‘o’ no nível 2 e a tecla ‘r’ no nível 3 têm mais de um filho. Em outras palavras, apenas 5 nós dos 27 têm dois ou mais filhos. As alternativas a esta estrutura abordam principalmente estas questões.
Antes de descrever a alternativa (PATRICIA Trie), vou responder à seguinte questão: porquê alternativas se podemos usar uma tabela de hash em vez de um array? Tabela de hash realmente ajuda a salvar a memória com pouca degradação de desempenho, mas não resolve o problema. Quanto mais alto você estiver no trie (mais próximo do nível zero), é mais provável que quase todos os caracteres em qualquer charset precisarão ser abordados. Tabelas de hash bem implementadas, como a de Java (definitivamente entre as melhores, sem dúvida as melhores), começam com um tamanho padrão e redimensionam automaticamente de acordo com um limite. Em Java o tamanho padrão é 16 com um limiar de 0.75 e duplica o seu tamanho em cada uma destas operações. Considerando Extended ASCII, quando o número de crianças em um nó atingir 192, a tabela de hash será redimensionada para 512, embora precisando apenas de 256 no final.
Radix Trie
Como PATRICIA Trie é um caso especial de Radix Trie, vou começar com este último. Na Wikipedia um Radix Trie é definido como “uma estrutura de dados que representa uma trie otimizada para o espaço… na qual cada nó que é o único filho é fundido com seu pai… Ao contrário das árvores regulares (onde chaves inteiras são comparadas em massa desde seu início até o ponto de desigualdade), a chave em cada nó é comparada pedaço de bits por pedaço de bits, onde a quantidade de bits naquele pedaço naquele nó é o radix r da trie do radix”. Esta definição fará mais sentido quando exemplificarmos esta trie na figura 3.
O número de crianças r de um nó em um radix trie é determinado pela seguinte fórmula onde x é o número de bits necessários para comparar o pedaço de bits acima mencionado:

A fórmula acima define o número de crianças em um Radix Trie para ser sempre um múltiplo de 2. Por exemplo, para um 4-Radix Trie, x = 2. Isto significa que teríamos que comparar pedaços de dois bits, um par de bits, porque com estes dois bits representamos todos os números decimais de 0 a 3, totalizando 4 números diferentes, um para cada criança.
Para entender melhor as definições acima, vamos considerar o exemplo da figura 3. Neste exemplo temos um conjunto hipotético de caracteres composto por 5 caracteres (NULL, A, B, C e D). Eu escolhi representá-los usando apenas 4 bits (tenha em mente que isto não tem nada a ver com r, um só precisa de 3 bits para representar 5 caracteres, mas tem a ver com a facilidade de desenhar o exemplo). No canto superior esquerdo da figura há uma tabela mapeando cada caractere para sua representação de bit.
Para inserir o caractere ‘A’, vou compará-lo bit a bit com o NULL. No canto superior direito da figura 3, dentro da caixa rotulada com 1 em um diamante amarelo, podemos ver que estes dois caracteres diferem no primeiro par. Este primeiro par é representado em vermelho na representação de 4 bits em A. Então DIFF contém a posição do bit onde o par diferente termina.
Para inserir o caracter ‘B’ precisamos compará-lo bit a bit com o caracter ‘A’. Esta comparação está na caixa diamantada rotulada com 2. A diferença cai desta vez sobre o segundo par de bits, em vermelho, que termina na posição 4. Como o segundo par é 01 criamos o nó com a chave B e apontamos o endereço 01 no nó A para ele. Este link pode ser visto na parte inferior da figura 3. O mesmo procedimento aplica-se para inserir os caracteres ‘C’ e ‘D’.

>
No exemplo acima vemos que o primeiro par (01 em azul) é o prefixo de todos os caracteres inseridos.
Este exemplo serve para descrever comparação de pedaços de bits, otimização de espaço (neste caso apenas quatro filhos, independentemente do tamanho do conjunto de caracteres) e fusão pai/filho (armazenado nos nós filhos apenas os bits que diferem da raiz) mencionados na definição do Radix Trie acima. No entanto, ainda há um link apontando para um nó nulo. A escassez é diretamente proporcional à profundidade de r e trie.
PATRICIA Trie
PATRICIA (Practical Algorithm to Retrieve Information Coded in Alphanumeric, Journal of the ACM, 15(4):514-534, October 1968) . Sim, PATRICIA é um acrônimo!
PATRICIA Trie é aqui definida por três regras:
- Cada nó (TWIN é o termo original da PATRICIA) tem duas crianças (r = 2 e x = 1 nos termos Radix Trie);
- Um nó só é dividido em um prefixo (L-PHRASE nos termos da PATRICIA) com duas crianças (cada criança formando uma BRANCH que é o termo original da PATRICIA) se duas palavras (PROPER OCCURRENCE nos termos da PATRICIA) compartilharem o mesmo prefixo; e
- Cada final de palavra será representada com um valor dentro do nó diferente do nulo (marca FIM na nomenclatura original da PATRICIA)
Regra número 2 acima implica que o comprimento do prefixo em cada nível é maior do que o comprimento do prefixo do nível anterior. Isto será muito importante nos algoritmos que suportam operações PATRICIA como inserir um elemento ou encontrar outro.
Das regras acima, pode-se definir o nó como ilustrado abaixo. Cada nó tem um pai, exceto a raiz, e dois filhos, um valor (qualquer tipo) e uma variável dif indicando a posição onde a divisão está na chave bitcode

Para usar o algoritmo PATRICIA precisamos de uma função que, dadas 2 cordas, retorne a posição do primeiro bit, da esquerda para a direita, onde elas diferem. Já vimos isso funcionando para Radix Trie.
Para operar o trie usando PATRICIA, ou seja, para inserir ou encontrar chaves nele, precisamos de 2 apontadores. Um é o pai, inicializado apontando-o para o nó raiz. O segundo é child, inicializado apontando-o para o filho esquerdo do root.
No que se segue a variável diff irá manter a posição onde a chave a ser inserida difere do child.key. Seguindo a regra número 2 definimos as 2 inequações seguintes:

>
>
Deixe os pontos encontrados para o nó onde termina a busca por uma chave. Se found.key for diferente da string que está sendo inserida, diff será computado, através de uma função ComputeDiff, usando esta string e found.key. Se forem iguais a chave existe na estrutura, e, como em qualquer tabela de símbolos, o valor deve ser retornado. Um método helper chamado BitAtPosition, que recupera o bit em uma posição específica (0 ou 1), será usado durante as operações.
Para pesquisar, precisamos definir uma função Search(key). Seu pseudo-código está na figura 4.

>
A segunda função que usaremos nesta história é a Insert(key). Seu pseudocódigo está na figura 6.

>
No pseudocódigo acima há um método para criar um nó chamado CreateNode. Seus argumentos podem ser entendidos a partir da figura 4.
>
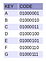
Para exemplificar como funciona um PATRICIA Trie, prefiro orientar o leitor numa operação passo a passo para completar a inserção de 7 caracteres (‘A’, ‘B’, ‘C’, ‘D’, ‘E’, ‘F’ e ‘G’ como especificado na figura 7 ao lado) na sua ordem natural. No final, espera-se que se tenha entendido como funciona esta estrutura de dados.
Carácter A é o primeiro a ser inserido. O seu código bitcode é 01000001. Como no Radix Trie, vamos comparar este bitcode com o da raiz, que neste momento é nulo, então comparamos 00000000 com 01000001. A diferença cai na posição 2 (aqui como x = 1 estamos comparando bit a bit ao invés de um par deles).

Para criar o nó precisamos apontar a criança esquerda e direita para seus respectivos sucessores. Como este nó é a raiz, por definição, seu filho esquerdo aponta para si mesmo enquanto seu filho direito aponta para a nulidade. Este será o único ponteiro nulo em toda a trindade. Lembrando que a raiz é o único nódulo sem pai. O valor, no nosso exemplo será inteiros imitando uma aplicação de contagem de palavras , é definido como 1. O resultado desta operação de inserção é mostrado na figura 8.
Próximo vamos inserir o caractere B com o bitcode 01000010. A primeira coisa é verificar se este caractere já está na estrutura. Para isso vamos procurar por ele. A pesquisa em um PATRICIA Trie é simples (veja o pseudocódigo na figura 5). Depois de comparar a chave da raiz com B conclui-se que são diferentes, por isso procedemos criando 2 indicadores: pai e filho. Inicialmente o pai aponta para a raiz e o filho aponta para o filho esquerdo da raiz. Neste caso ambos os pontos apontam para o nó A. Seguindo a regra número 2, vamos iterar a estrutura enquanto a inequação (1) é verdadeira.
Neste momento parent.DIFF é igual a, e não inferior a, child.DIFF. Isto quebra a inequação (1). Como a criança.VALUE é diferente de null (igual a 1), comparamos os caracteres. Como A é diferente de B, isto significa que B não está na trie e precisa ser inserido.
Para inserir começamos, novamente, a definir pai e filho como antes, ou seja, pai aponta para a raiz e filho aponta para o seu nó esquerdo. A iteração através da estrutura deve seguir as inequações (1) e (2). Continuamos calculando dif, que é a diferença, bitwise, entre B e child.KEY, que neste estágio é igual a A (diferença entre os códigos bit 01000001 e 01000010) . A diferença cai sobre o bit na posição 7 , portanto dif = 7,

>
Neste momento pai e filho apontam para o mesmo nó (para o nó A, a raiz). Como a iniquação (1) já é falsa e child.DIFF é menos que dif, vamos criar o nó B e apontar o parent.LEFT para ele. Como fizemos com o nó A, precisamos apontar os filhos do nó B para algum lugar. O bit na posição 7 em B é 1, então o filho direito do nó B apontará para si mesmo. A criança B esquerda do nó B apontará para os pais, a raiz neste caso. O resultado final é mostrado na figura 9.
Ao apontar o filho B esquerdo do nó para seu pai, estamos habilitando a divisão mencionada na regra número 2. Quando inserimos um caractere cuja diferença cai entre 2 e 7 este ponteiro nos enviará de volta para a posição correta a partir da qual se insere o novo caractere. Isso acontecerá quando inserirmos o caractere D.
Mas antes disso precisamos inserir o caractere C com bitcode igual a 01000011. O ponteiro pai apontará para o nó A (a raiz). Desta vez, diferente de quando estávamos procurando pelo caractere B, child aponta para o nó B (naquele momento ambos os ponteiros estavam apontando para a raiz).
Neste momento a inércia (1) se mantém (parent.DIFF é menor que child.DIFF) então atualizamos ambos os ponteiros, definindo parent para child e child para o filho direito do nó B porque na posição 7 C o bit é 1.
Após a atualização ambos os ponteiros apontam para o nó B, quebrando a inércia (1). Como fizemos antes, comparamos o bitcode child.KEY com o bitcode de C (01000010 com 01000011), concluindo que eles diferem na posição 8. Como na posição 7 o bit de C é 1, este novo nó (nó C) será o filho direito de B. Na posição 8 o bit de C é 1, fazendo-nos definir o filho direito do nó C para si mesmo, enquanto que o filho esquerdo aponta para o pai, neste momento o nó B. O trie resultante está na figura 10.

>
Nexterno caractere é D (código de bit 01000100). Como fizemos com a inserção do caractere C, vamos definir inicialmente o ponteiro pai para o nó A e o ponteiro filho para o nó B. Inequação (1) é válida, então atualizamos os ponteiros. Agora pai aponta para o nó B e filho aponta para o filho esquerdo do nó B, porque na posição 7, o bit de D é 0. Diferente da inserção do caractere C, agora filho aponta de volta para o nó A, quebrando a iniquação (1). Novamente calculamos a diferença entre os bitcodes A e D. Agora dif é 6. Mais uma vez definimos pai e filho como normalmente fazemos. Agora, enquanto a inequação (1) é válida, a inequação (2) não é. Isto implica que vamos inserir D como a criança esquerda de A. Mas e os filhos de D? Na posição 6 D’s bit é 1, então é a criança direita aponta para si mesma. A parte interessante é que o filho esquerdo do nó D agora aponta para o nó B atingindo o trie desenhado na figura 11.

Nexterno é o caractere E com o bitcode 01000101. A função Busca retornará o nó D. A diferença entre os caracteres D e E cai sobre o bit na posição 8. Como na posição 6 o bit de E é 1, ele será posicionado à direita de D. A estrutura do trie é ilustrada na figura 12.

>
O interessante de inserir o caractere F é que o seu lugar é entre os caracteres D e E, porque a diferença entre D e F está na posição 7. Mas na posição 7 o bit de E é 0, então o nó E será o filho esquerdo do nó F. A estrutura está agora ilustrada na figura 13.

>
E, finalmente, inserimos o caractere G. Após todos os cálculos concluímos que o novo nó deve ser colocado como o filho direito do nó F com dif é igual a 8. O resultado final está na figura 14.

>
Até agora estamos inserindo cordas compostas de apenas um caractere. O que aconteceria se tentássemos inserir as cordas AB e BA? O leitor interessado pode tomar esta proposta como um exercício. Duas dicas: ambas as cordas diferem do nó B na posição 9; e a triagem final é ilustrada na figura 15.

Pensando sobre a última figura, a seguinte pergunta pode ser feita: Para encontrar, por exemplo, a string BA são necessárias comparações de 5 bits, enquanto para calcular o código hash desta string são necessárias apenas duas iterações, então quando é que o PATRICIA Trie se torna competitivo? Imagine se inserirmos nesta estrutura a string ABBABABBBBBABBA (tirada do exemplo do artigo original da PATRICIA de 1968) que tem 16 caracteres? Esta string seria colocada como a filha esquerda do nó AB com dif na posição 17. Para encontrá-la, precisaríamos de comparações de 5 bits, enquanto para calcular o código hash seriam necessárias 16 iterações, uma para cada caracter, sendo esta a razão pela qual PATRICIA Tries são tão competitivos ao pesquisar long strings.
PATRICIA Trie vs Hash Map
Nesta última seção vou comparar Hash Map e PATRICIA Trie em duas aplicações. A primeira é uma contagem de palavras em leipzig1m.txt contendo 1 milhão de frases aleatórias e a segunda é preenchendo uma tabela de símbolos com mais de 2,3 milhões de URLs do projeto DMOZ (fechado em 2017) baixado daqui.
O código que desenvolvi e usei para implementar o pseudocódigo acima e comparar o desempenho do PATRICIA Trie com a Tabela de Hash pode ser encontrado no meu GitHub.
Estas comparações foram executadas na minha caixa Ubuntu 18.04. A configuração pode ser encontrada na figura 16