ORDER STATA
Markov-växlingsmodeller
Highlights
- Markov-övergångsmodellering
- Autoregressiv modell
- Dynamisk regressionsmodell
- Statsberoende regressionsparametrar
- Stats-beroende variansparametrar
- Tabeller med
- Övergångssannolikheter
- Förväntade tillståndslängder
-
- Prediktioner
- Förväntade värden för beroende variabel
- Sannolikheterna för att befinna sig i ett tillstånd
- Statisk (ett-steg)
- Dynamisk (flera steg)
- RMSE för förutsägelser
- Autoregressiv modell
- Dynamisk regressionsmodell
- Övergångssannolikheter
- Förväntade tillståndslängder
- Förväntade värden för beroende variabel
- Sannolikheterna för att befinna sig i ett tillstånd
- Statisk (ett-steg)
- Dynamisk (flera steg)
- RMSE för förutsägelser
Vad handlar det här om?
Ibland utvecklas processer över tid med diskreta förändringar i resultaten.
Tänk på ekonomiska recessioner och expansioner. I början av en recession sjunker produktionen och sysselsättningen och förblir låg, för att senare öka produktionen och sysselsättningen. Tänk på bipolära sjukdomar där det finns maniska perioder som följs av depressiva perioder, och processen upprepas. Statistiskt sett förändras medelvärden, varianser och andra parametrar mellan olika episoder (regimer). Vårt problem är att uppskatta när regimerna förändras och värdena på de parametrar som är förknippade med varje regim. Att fråga när regimer förändras är likvärdigt med att fråga hur länge regimer består.
I Markov-övergångsmodeller uppskattar vi förutom medelvärdena, varianserna etc. för varje regim även sannolikheten för regimskifte. De uppskattade övergångssannolikheterna för ett visst problem kan vara följande:
| från/till | ||||
| stat | . 1 2 | |||
| 1 | 0.82 0,18 | |||
| 2 | 0,75 0,25 | |||
Start i tillstånd 1. Sannolikheten att övergå från tillstånd 1 till tillstånd 1 är 0,82. Med andra ord, när processen väl befinner sig i tillstånd 1 tenderar den att stanna där. Med en sannolikhet på 0,18 övergår processen dock till tillstånd 2. Tillstånd 2 är inte lika långvarigt. Med en sannolikhet på 0,75 återgår processerna från tillstånd 2 till tillstånd 1 under nästa tidsperiod.
Markov-skiftande modeller är inte begränsade till två regimer, även om modeller med två regimer är vanliga.
I exemplet ovan beskrev vi växlingen som abrupt; sannolikheten ändrades omedelbart. Sådana Markovmodeller kallas dynamiska modeller. Markovmodeller kan också rymma mjukare förändringar genom att modellera övergångssannolikheterna som en autoregressiv process.
Växlingen kan alltså vara jämn eller plötslig.
Vi ska se hur det fungerar
Låt oss titta på medelvärdesförändringar mellan olika regimer. Vi kommer särskilt att analysera Federal Funds Rate. Federal Funds Rate är den ränta som USA:s centralbank tar ut av affärsbankerna för lån över natten. Vi kommer att titta på förändringar i Federal Funds Rate från 1954 till slutet av 2010. Här är uppgifterna:
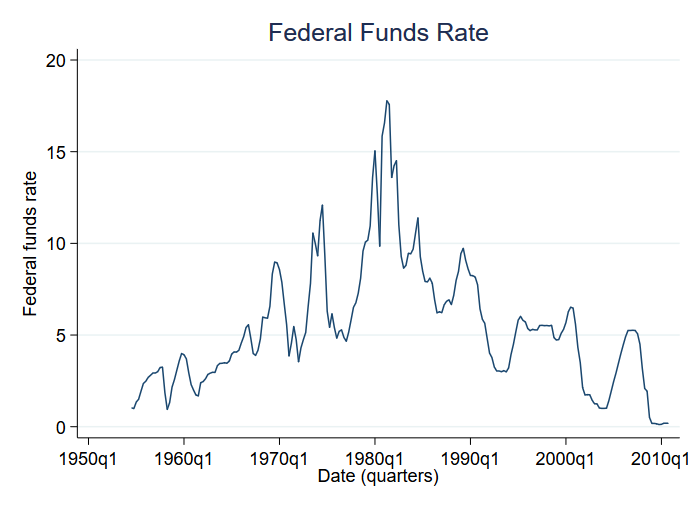
Vi har kvartalsvisa uppgifter. Höga räntor verkar känneteckna sjuttio- och åttiotalen. Vi kommer att anta att det finns en annan regim för lägre räntor som tycks känneteckna de andra decennierna.
För att anpassa en modell med dynamisk växling (abrupt förändring) med två regimer skriver vi
. mswitch dr fedfundsPerforming EM optimizaton:Performing gradient-based optimization:
| Iteration 0: | loglikelihood = -508.66031 |
| Iteration 1: | log sannolikhet = -508.6382 |
| Iteration 2: | log sannolikhet = -508.63592 |
| Iteration 3: | log sannolikhet = -508.63592 |
Markov-switching dynamisk regressionSampel: 1954q3 – 2010q4 Nr. obs = 226Antal stater = 2 AIC = 4,5455Ovillkorliga sannolikheter: övergång HQIC = 4,5760 SBIC = 4,6211Loglikelihood = -508.63592
| fedfunds | Coef. Std. Err. z P>|z| | ||
| State1 | |||
| _cons | 3.70877 .1767083 20.99 0.000 3.362428 4.055112 | ||
| State2 | |||
| _cons | 9.556793 .2999889 31.86 0.000 8.968826 10.14476 | ||
| sigma | 2.107562 .1008692 1.918851 2.314831 | ||
| p11 | .9820939 .0104002 .9450805 .9943119 | ||
| p21 | .0503587 .0268434 .0173432 .1374344 | ||
I resultatet ovan redovisas
- medelvärdena för de två tillstånden (_cons);
- en enda standardavvikelse för hela processen (sigma); och
- övergångssannolikheterna för tillstånd 1 till 1 och tillstånd 2 till 1 (p11 och p21).
Tillstånd1 är det måttliga tillståndet (medelvärde 3,71 %).
State2 är state2 är high-rate state (medelvärde 9,56 %).
| från/till | ||||
| stat | . 1 2 | |||
| 1 | 0.98 1 – 0,98 | |||
| 2 | 0,05 1 – 0,05 | |||
Båda tillstånden är otroligt bestående (sannolikheterna 1->1 och 2->2 på 0,98 och 0,95).
Bland de saker man kan förutsäga efter skattning är sannolikheten att befinna sig i de olika tillstånden. Vi har bara två tillstånd, och därför säger sannolikheten för att befinna sig i (säg) tillstånd 2 oss sannolikheten för båda tillstånden. Vi kan få fram den förutspådda sannolikheten och grafera den tillsammans med de ursprungliga uppgifterna:
. predict prfed, pr
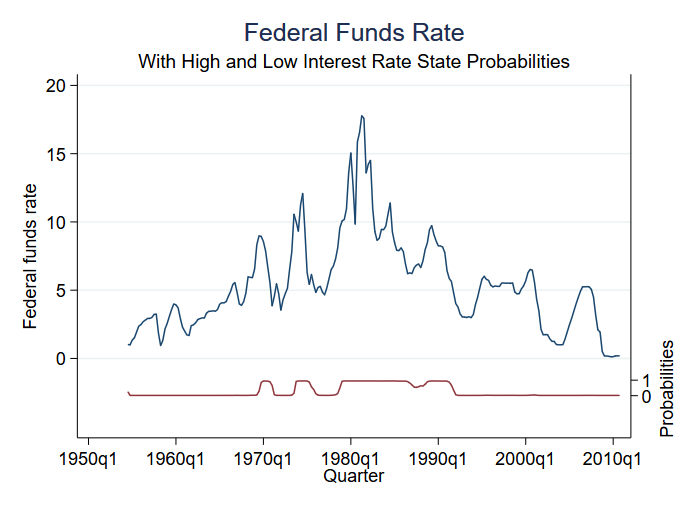
Modellen har liten osäkerhet om regimen vid varje tidpunkt. Vi ser tre perioder med höga regimer och fyra perioder med måttliga regimer.
Låt oss se hur det fungerar
Låt oss titta på ett exempel på sjukdomsutbrott, nämligen påssjuka per 10 000 invånare i New York City mellan 1929 och 1972. Man skulle kunna tro att utbrott motsvarar förändringar i medelvärdet, men vad vi ser i data är en ännu större förändring i variansen:
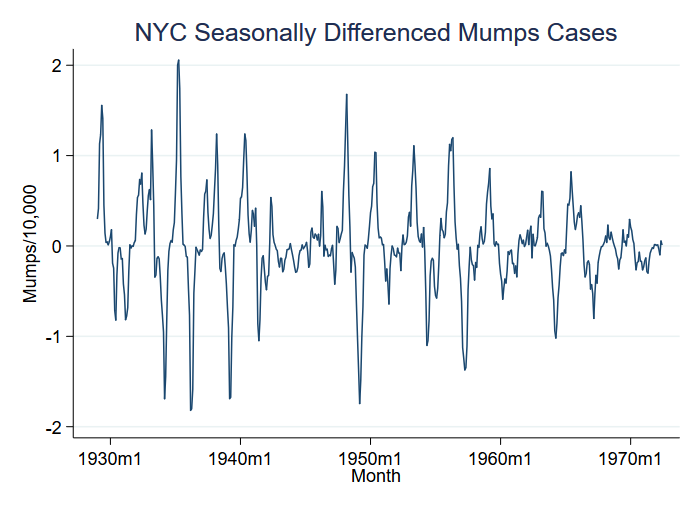
Vi har grafiskt redovisat variabeln S12.mumpspc, dvs. säsongsmässigt differentierade fall av påssjuka per capita under en tolvmånadersperiod, och vi kommer att analysera S12.mumpspc.
Vi kommer att anta två regimer där medelvärdet och variansen för S12.mumpspc förändras. För att anpassa en dynamisk modell (abrupt förändring) skriver vi
. mswitch dr S12.mumpspc, varswitch switch(LS12.mumpspc, noconstant)Performing EM optimizaton:Performing gradient-based optimization:
| Iteration 0: | log sannolikhet = 110,9372 (inte konkav) | |
| Iteration 1: | log sannolikhet = 120.68028 | |
| Iteration 2: | log sannolikhet = 123.23244 | |
| Iteration 3: | log sannolikhet = 131.47084 | |
| Iteration 3: | log sannolikhet = 131.72182 | |
| Iteration 3: | log sannolikhet = 131.7225 | |
| Iteration 3: | log sannolikhet = 131.7225 | |
Markov-omkoppling dynamisk regressionSampel: 1929m2 – 1972m6 Nr. obs = 521Antal tillstånd = 2 AIC = -0.4826Ovillkorliga sannolikheter: övergång HQIC = -0.4634 SBIC = -0.4336Loglikelihood = 131.7225
| S12.mumspc | Coef. Std. Err. z P>|z| | |||
| State1 | ||||
| mumpspc | ||||
| LS12. | .4202751 .0167461 25.10 0.000 .3874533 .4530968 | |||
| State2 | ||||
| mumpspc | ||||
| LS12. | .9847369 .0258383 38.11 0.000 .9340947 1.035379 | |||
| sigma1 | .0562405 .0050954 .0470901 .067169 | |||
| sigma2 | .2611362 .0111191 .2402278 .2838644 | |||
| p11 | .762733 .0362619 .6846007 .8264175 | |||
| p12 | .1473767 .0257599 .1036675 .205294 | |||
Rapporterat är
- medelvärdena för de två tillstånden för S12.mumpspc (0,42 och 0,98);
- standardavvikelserna för de två tillstånden (0,06 och 0,26); och
- övergångssannolikheterna för tillstånd 1 till 1 och tillstånd 2 till 1 (0,76 och 0,15).
Tillstånd 1 är tillståndet med låg varians.
Den fullständiga uppsättningen övergångssannolikheter är följande: