En multiplexer är en kombinationskrets som har 2n ingångslinjer och en enda utgångslinje. Helt enkelt är multiplexern en kombinationskrets med flera ingångar och en enda utgång. Den binära informationen tas emot från ingångslinjerna och leds till utgångslinjen. På grundval av värdena på urvalslinjerna kopplas en av dessa dataingångar till utgången.
Till skillnad från kodare och avkodare finns det n urvalslinjer och 2n ingångslinjer. Det finns alltså totalt 2N möjliga kombinationer av ingångar. En multiplexer behandlas också som Mux.
Det finns olika typer av multiplexer som är följande:
2×1 Multiplexer:
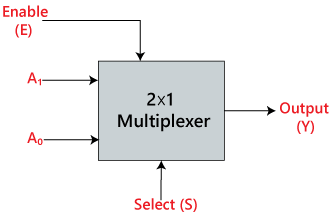
I 2×1 multiplexer finns det bara två ingångar, dvs, A0 och A1, en vallinje, dvs. S0, och en enda utgång, dvs. Y. På grundval av den kombination av ingångar som finns vid vallinjen S0 kommer en av dessa två ingångar att anslutas till utgången. Blockdiagrammet och sanningstabellen för 2×1-multiplexern ges nedan.
Blockdiagram:
Sanningstabell:
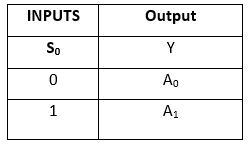
Det logiska uttrycket för termen Y är som följer:
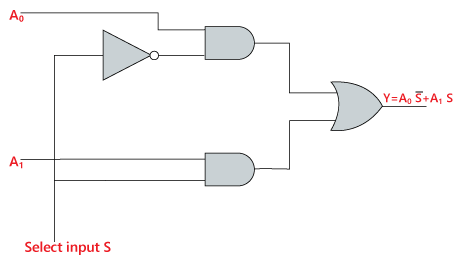
Y=S0′.A0+S0.A1
Den logiska kretsen för ovanstående uttryck ges nedan:
4×1 Multiplexer:
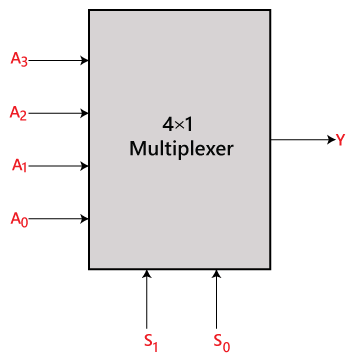
I 4×1 multiplexern finns det totalt fyra ingångar, dvs, A0, A1, A2 och A3, två urvalsledningar, dvs. S0 och S1, och en enda utgång, dvs. Y. På grundval av den kombination av ingångar som finns vid urvalsledningarna S0 och S1 ansluts en av dessa fyra ingångar till utgången. Blockdiagrammet och sanningstabellen för 4×1-multiplexern ges nedan.
Blockdiagram:
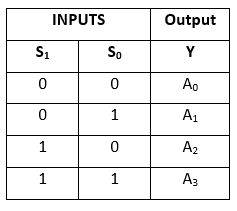
Sanningstabell:
Det logiska uttrycket för termen Y är följande:
Y=S1′ S0′ A0+S1′ S0 A1+S1 S0′ A2+S1 S0 A3
Den logiska kretsen för ovanstående uttryck ges nedan:
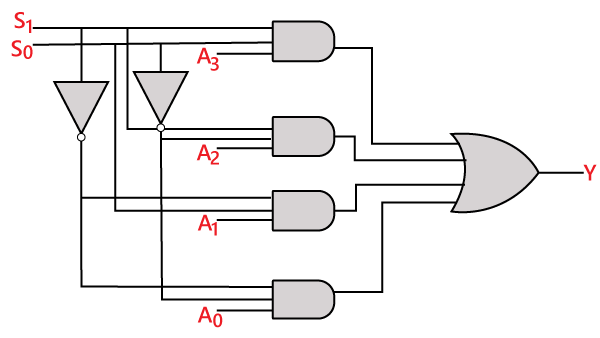
8-till-1-multiplexer
I en 8-till-1-multiplexer finns det totalt åtta ingångar, dvs.e., A0, A1, A2, A3, A4, A5, A6 och A7, tre urvalsledningar, dvs. S0, S1 och S2 och en enda utgång, dvs. Y. På grundval av den kombination av ingångar som finns vid urvalsledningarna S0, S1 och S2 ansluts en av dessa åtta ingångar till utgången. Blockdiagrammet och sanningstabellen för 8×1-multiplexern ges nedan.
Blockdiagram:

Sanningstabell:
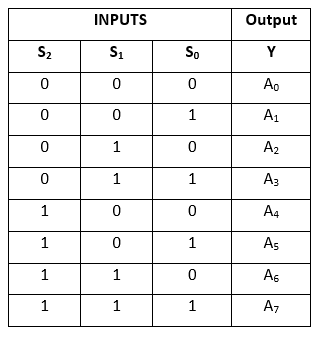
Det logiska uttrycket för termen Y är följande:
Y=S0′.S1′.S2′.A0+S0.S1′.S2′.A1+S0′.S1.S2′.A2+S0.S1.S2′.A3+S0′.S1′.S2 A4+S0.S1′.S2 A5+S0′.S1.S2 .A6+S0.S1.S3.A7
Den logiska kretsen för ovanstående uttryck ges nedan:
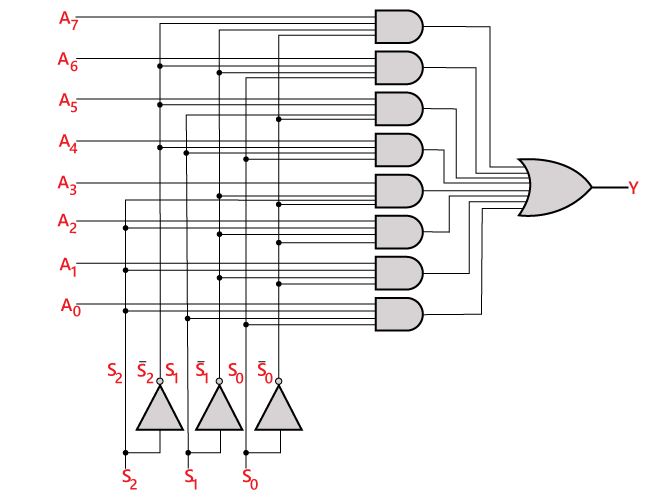
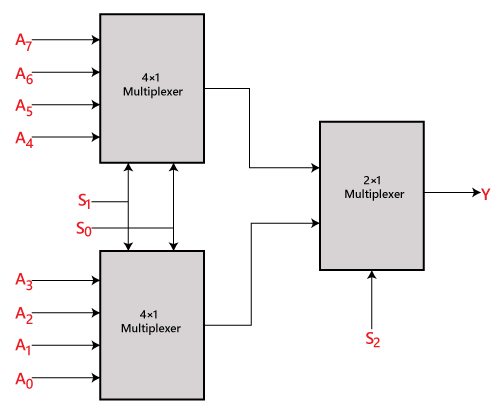
8×1 multiplexer med hjälp av 4×1- och 2×1-multiplexer
Vi kan implementera 8×1-multiplexern med hjälp av en lägre ordning multiplexer. För att implementera 8×1-multiplexern behöver vi två 4×1-multiplexer och en 2×1-multiplexer. 4×1-multiplexern har 2 urvalsledningar, 4 ingångar och 1 utgång. 2×1-multiplexern har endast en urvalsledning.
För att få 8 dataingångar behöver vi två 4×1-multiplexer. 4×1-multiplexern ger en utgång. För att få den slutliga utgången behöver vi alltså en 2×1 multiplexer. Blockdiagrammet för en 8×1 multiplexer som använder 4×1 och 2×1 multiplexer visas nedan.
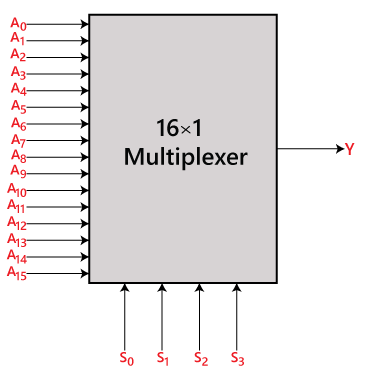
16 till 1 multiplexer
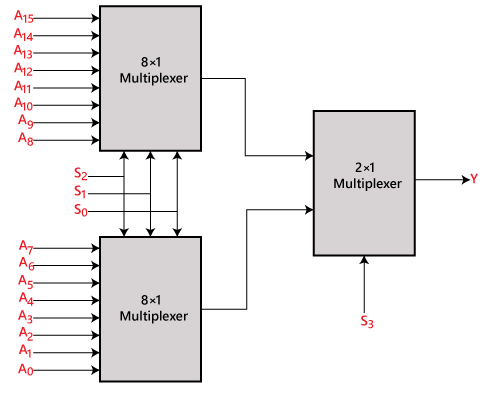
I en 16 till 1 multiplexer finns det totalt 16 ingångar, dvs. A0, A1, …, A16, 4 urvalsledningar, dvs, S0, S1, S2 och S3 och en enda utgång, dvs. Y. På grundval av den kombination av ingångar som finns vid urvalsledningarna S0, S1 och S2 kommer en av dessa 16 ingångar att anslutas till utgången. Blockdiagrammet och sanningstabellen för 16×1
Blockdiagram:
Sanningstabell:
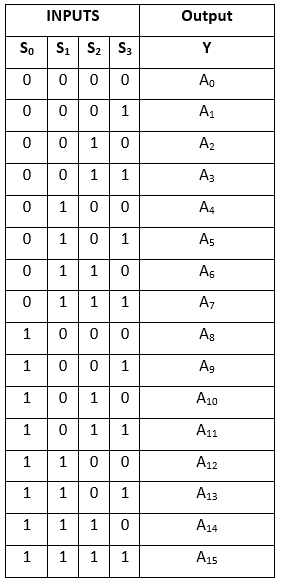
Det logiska uttrycket för termen Y är följande:
Den logiska kretsen för ovanstående uttryck ges nedan:
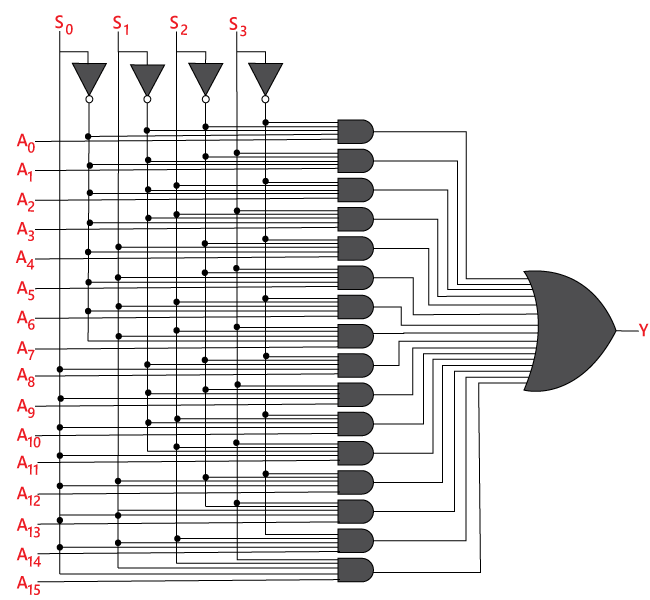
16×1 multiplexer med hjälp av 8×1 och 2×1 multiplexer
Vi kan implementera 16×1 multiplexern med hjälp av en multiplexer av lägre ordning. För att implementera 8×1-multiplexern behöver vi två 8×1-multiplexer och en 2×1-multiplexer. 8×1-multiplexern har 3 urvalsledningar, 4 ingångar och 1 utgång. 2×1-multiplexern har endast en urvalsledning.
För att få 16 dataingångar behöver vi två 8×1-multiplexer. Den 8×1 multiplexern ger en utgång. För att få den slutliga utgången behöver vi alltså en 2×1 multiplexer. Blockdiagrammet för 16×1 multiplexer som använder 8×1 och 2×1 multiplexer ges nedan.