În microcosmosul în care sunt integrat, structura de date Trie nu este atât de populară. Acest mediu este compus în principal din cercetători de date și, într-un număr mai mic, ingineri de software, care lucrează cu procesarea limbajului natural (NLP).
Recent, m-am trezit într-o discuție interesantă despre când să folosesc trie sau hash table. Deși nu a fost nimic nou în acea discuție pe care să îl pot relata aici, cum ar fi avantajele și dezavantajele fiecăreia dintre aceste două structuri de date (dacă căutați puțin pe Google veți găsi multe link-uri care le abordează), ceea ce a fost nou pentru mine a fost un tip special de trie numit Patricia Trie și, că în anumite scenarii, această structură de date are performanțe comparabile atât în timp de procesare cât și în spațiu cu hash table, în timp ce abordează sarcini precum listarea șirurilor de caractere cu prefix comun fără costuri suplimentare.
Cu acest lucru în minte, am căutat o poveste sau un blog care să mă ajute să înțeleg într-un mod simplu (eufemism pentru lene) cum funcționează algoritmul PATRICIA, servind în mod special ca o scurtătură pentru a citi lucrarea de 21 de pagini publicată în 1968. Din nefericire, nu am reușit în această căutare, rămânând fără alternativă la citirea ei.
Obiectivul meu cu această povestire este de a umple golul de mai sus, adică de a avea o povestire care să descrie în termeni simpli algoritmul de față.
Pentru a-mi atinge obiectivul, mai întâi, și pe scurt, voi prezenta, pentru cei care nu sunt familiarizați cu încercările, această structură de date. După această introducere, voi enumera cele mai populare trie existente, permițându-mi să implementez și să descriu în detaliu modul în care funcționează PATRICIA Trie și de ce sunt atât de performante. Voi încheia această poveste comparând rezultatele (performanță și consum de spațiu) în două aplicații diferite: prima este o numărătoare de cuvinte (<WORD, FREQUENCY> tuple) bazată pe un text destul de mare; iar a doua este construirea unui <URL, IP> tuple, bazat pe o listă de peste 2 milioane de URL-uri, care constă în elementul central al unui server DNS. Ambele aplicații au fost construite pe baza Hash Map și Patricia Trie.
După cum sunt definite de Sedgewick și Wayne de la Universitatea Princeton în cartea lor Algorithms – Fourth Edition (editor: Addison-Wesley), un trie, sau arbore de prefixe, este „o structură de date construită din caracterele cheii de căutare pentru a ghida căutarea”. Această „structură de date este compusă din noduri care conține legături care sunt fie nule, fie fac trimitere la alte noduri. Fiecare nod este indicat de un singur alt nod, care se numește părintele său (cu excepția unui nod, rădăcina, care nu are noduri care să-l indice), iar fiecare nod are S legături, unde S este dimensiunea alfabetului (sau a setului de caractere)”.
Figura 1 de mai jos, după definiția de mai sus, conține un exemplu de trie.

Nodul rădăcină nu are etichetă. Acesta are trei copii: noduri cu cheia „a”, „h” și „s”. În colțul din dreapta jos al figurii există un tabel care enumeră toate cheile cu valoarea lor respectivă. De la rădăcină putem trece la ‘a’ -> ‘i’ -> ‘r’. Această secvență formează cuvântul „aer” cu o valoare (de exemplu, numărul de apariții ale acestui cuvânt într-un text) de 4 (valorile se află în interiorul unei cutii verzi). Prin convenție, un cuvânt existent într-un tabel de simboluri are o valoare care nu este nulă. Așadar, deși cuvântul „airway” există în limba engleză, el nu se află în această trie, deoarece, conform convenției, valoarea nodului cu cheia „y” este nulă.
Vorba „air” este, de asemenea, prefixul cuvintelor: „avion”; și „căi aeriene”. Secvența ‘h’ -> ‘a’ formează prefixul cuvintelor „are” și „pălărie”, așa cum secvența ‘h’ -> ‘o’ formează prefixul cuvintelor „casă” și „cal”.
Pe lângă faptul că servește bine ca structură de date pentru, să zicem, un dicționar, servește, de asemenea, ca un element important al unei aplicații de completare. Un sistem ar putea propune cuvintele „avion” și „căi aeriene” după ce un utilizator a tastat cuvântul „aer”, prin parcurgerea subarborelui a cărui rădăcină este nodul cu cheia „r”. Un avantaj suplimentar al acestei structuri este faptul că se poate obține o listă ordonată a cheilor existente, fără costuri suplimentare, prin parcurgerea trie în ordine, stivuind copiii unui nod și parcurgându-i de la stânga la dreapta.
În figura 2 este exemplificată anatomia nodului.

Partea interesantă în această anatomie este că indicatorii copiilor sunt de obicei stocați într-o matrice. Dacă reprezentăm un set de caractere S de, de exemplu, Extended ASCII, avem nevoie ca array-ul să fie de dimensiunea 256. Având un caracter copil, putem accesa pointerul său în părintele său în timp O(1). Având în vedere că dimensiunea vocabularului este N și că dimensiunea celui mai lung cuvânt este M, adâncimea trie este de asemenea M și este nevoie de O(MN) pentru a parcurge structura. Dacă luăm în considerare faptul că, în mod normal, N este mult mai mare decât M (numărul de cuvinte dintr-un corpus este mult mai mare decât dimensiunea celui mai lung cuvânt), putem considera că O(MN) este liniar. În practică, această matrice este rarefiată, adică majoritatea nodurilor au mult mai puțini copii decât S. În plus, dimensiunea medie a cuvintelor este, de asemenea, mai mică decât M, astfel că, în practică, în medie, este nevoie de O(logₛ N) pentru a căuta o cheie și de O(N logₛ N) pentru a parcurge întreaga structură.
Există două probleme principale cu această structură de date. Una este consumul de spațiu. La fiecare nivel L, începând cu zero, există, asimptotic, Sᴸ pointeri. Dacă în cazul ASCII extins, adică 256 de caractere, aceasta este o problemă în cazul dispozitivelor cu memorie limitată, situația se înrăutățește dacă se iau în considerare toate caracterele Unicode (65.000 de caractere). A doua este cantitatea de noduri cu un singur copil, ceea ce degradează performanța de introducere și căutare. În exemplul din figura 1, numai rădăcina, cheia „h” de la nivelul 1, cheile „a” și „o” de la nivelul 2 și cheia „r” de la nivelul 3 au mai mult de un copil. Cu alte cuvinte, doar 5 noduri din cele 27 au doi sau mai mulți copii. Alternativele la această structură abordează în principal aceste probleme.
Printre altele, înainte de a descrie alternativa (PATRICIA Trie), voi răspunde la următoarea întrebare: de ce alternative dacă putem folosi un tabel hash în loc de o matrice? Tabelul hash ajută într-adevăr la economisirea memoriei cu o mică degradare a performanței, dar nu rezolvă problema. Cu cât vă aflați mai sus în trie (mai aproape de nivelul zero), este mai probabil ca aproape toate caracterele din orice set de caractere să trebuiască să fie abordate. Tabelele hash bine implementate, precum cea din Java (cu siguranță printre cele mai bune, fără îndoială cea mai bună), încep cu o dimensiune implicită și se redimensionează automat în funcție de un prag. În Java, dimensiunea implicită este de 16 cu un prag de 0,75 și își dublează dimensiunea la fiecare dintre aceste operații. Luând în considerare Extended ASCII, în momentul în care numărul de copii dintr-un nod ajunge la 192, tabelul hash va fi redimensionat la 512, chiar dacă are nevoie de doar 256 la final.
Radix Trie
Cum PATRICIA Trie este un caz special de Radix Trie, voi începe cu acesta din urmă. În Wikipedia, un Radix Trie este definit ca fiind „o structură de date care reprezintă o trie optimizată din punct de vedere spațial… în care fiecare nod care este singurul copil este fuzionat cu părintele său… Spre deosebire de arborii obișnuiți (unde cheile întregi sunt comparate în masă de la începutul lor până la punctul de inegalitate), cheia de la fiecare nod este comparată bucată cu bucată de biți, unde cantitatea de biți din acea bucată la acel nod este radix r al radix trie”. Această definiție va avea mai mult sens atunci când vom exemplifica această trie în figura 3.
Numărul de copii r al unui nod dintr-o trie radix este determinat de următoarea formulă în care x este numărul de biți necesari pentru a compara bucățile de biți menționate mai sus:

Formula de mai sus stabilește că numărul de copii dintr-o trie radix este întotdeauna un multiplu de 2. De exemplu, pentru un Trie Radix 4, x = 2. Acest lucru înseamnă că ar trebui să comparăm bucăți de doi biți, o pereche de biți, deoarece cu acești doi biți reprezentăm toate numerele zecimale de la 0 la 3, totalizând 4 numere diferite, câte unul pentru fiecare copil.
Pentru a înțelege mai bine definițiile de mai sus, să luăm în considerare exemplul din figura 3. În acest exemplu avem un set de caractere ipotetic format din 5 caractere (NULL, A, B, C și D). Am ales să le reprezint folosind doar 4 biți (rețineți că acest lucru nu are nimic de-a face cu r, sunt necesari doar 3 biți pentru a reprezenta 5 caractere, ci are de-a face cu ușurința de a desena exemplul). În colțul din stânga sus al figurii există un tabel care mapează fiecare caracter cu reprezentarea lui pe biți.
Pentru a introduce caracterul „A”, îl voi compara pe biți cu cel NULL. În colțul din dreapta sus al figurii 3, în interiorul căsuței etichetate cu 1 într-un romb galben, putem vedea că aceste două caractere diferă la prima pereche. Această primă pereche este reprezentată cu roșu în reprezentarea pe 4 biți a lui A. Așadar, DIFF conține poziția bitului în care se termină perechea diferită.
Pentru a introduce caracterul „B” trebuie să îl comparăm bit cu bit cu caracterul „A”. Această comparație se află în căsuța rombică etichetată cu 2. Diferența cade de data aceasta pe a doua pereche de biți, în roșu, care se termină în poziția 4. Deoarece cea de-a doua pereche este 01, creăm nodul cu cheia B și îi indicăm adresa 01 din nodul A. Această legătură poate fi observată în partea de jos a figurii 3. Aceeași procedură se aplică pentru inserarea caracterelor „C” și „D”.

În exemplul de mai sus vedem că prima pereche (01 în albastru) este prefixul tuturor caracterelor inserate.
Acest exemplu servește pentru a descrie compararea chunk-of-bits, optimizarea spațiului (doar patru copii în acest caz, indiferent de mărimea setului de caractere) și fuziunea părinte/copil (stocat la nodurile copii doar biții care diferă de rădăcină) menționate în definiția Radix Trie de mai sus. Cu toate acestea, există încă o legătură care indică un nod nul. Sparseness este direct proporțională cu r și cu adâncimea trie-ului.
PATRICIA Trie
PATRICIA (Practical Algorithm to Retrieve Information Coded in Alphanumeric, Journal of the ACM, 15(4):514-534, octombrie 1968) . Da, PATRICIA este un acronim!
PATRICIA Trie este definită aici prin trei reguli:
- Care nod (TWIN este termenul original al lui PATRICIA) are doi copii (r = 2 și x = 1 în termenii Radix Trie);
- Un nod este împărțit într-un prefix (L-PHRASE în termenii lui PATRICIA) cu doi copii (fiecare copil formând o BRANCH care este termenul original al lui PATRICIA) numai dacă două cuvinte (PROPER OCCURRENCE în termenii lui PATRICIA) au același prefix; și
- Care cuvânt care se termină va fi reprezentat cu o valoare în cadrul nodului diferită de nul (marca END în nomenclatura originală a PATRICIEI)
Regula numărul 2 de mai sus presupune ca lungimea prefixului de la fiecare nivel să fie mai mare decât lungimea prefixului de la nivelul anterior. Acest lucru va fi foarte important în algoritmii care susțin operațiile PATRICIA, cum ar fi inserarea unui element sau găsirea altuia.
Din regulile de mai sus se poate defini nodul așa cum este ilustrat mai jos. Fiecare nod are un părinte, cu excepția rădăcinii, și doi copii, o valoare (de orice tip) și o variabilă diff care indică poziția în care se află divizarea în cheia bitcode

Pentru a utiliza algoritmul PATRICIA avem nevoie de o funcție care, date fiind 2 șiruri de caractere, returnează poziția primului bit, de la stânga la dreapta, în care acestea diferă. Am văzut deja că acest lucru funcționează pentru Radix Trie.
Pentru a opera trie folosind PATRICIA, adică pentru a introduce sau găsi chei în ea, avem nevoie de 2 pointeri. Unul este părinte, inițializat prin îndreptarea lui către nodul rădăcină. Al doilea este child, inițializat prin îndreptarea lui către copilul stâng al rădăcinii.
În ceea ce urmează, variabila diff va reține poziția în care cheia care se inserează diferă de child.key. Urmând regula numărul 2, definim următoarele 2 inecuații:

Let found indică nodul în care se termină căutarea unei chei. Dacă found.key este diferit de șirul care se introduce, se va calcula diff, prin intermediul unei funcții ComputeDiff, folosind acest șir și found.key. Dacă acestea sunt egale, cheia există în structură și, ca în orice tabel de simboluri, trebuie returnată valoarea. O metodă ajutătoare numită BitAtPosition, care recuperează bitul dintr-o anumită poziție (0 sau 1), va fi utilizată în timpul operațiilor.
Pentru a căuta trebuie să definim o funcție Search(key). Pseudocodul acesteia este în figura 4.

A doua funcție pe care o vom folosi în această poveste este Insert(key). Pseudocodul acesteia este în figura 6.

În pseudocodul de mai sus există o metodă de creare a unui nod numită CreateNode. Argumentele sale pot fi înțelese din figura 4.
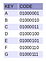
Pentru a exemplifica modul în care funcționează un Trie PATRICIA, prefer să ghidez cititorul într-o operațiune pas cu pas pentru a finaliza inserarea a 7 caractere („A”, „B”, „C”, „D”, „E”, „F” și „G”, așa cum se specifică în figura 7 alăturată) în ordinea lor naturală. La final, sperăm că se va fi înțeles cum funcționează această structură de date.
Caracterul A este primul care trebuie inserat. Codul său binar este 01000001. Ca și în cazul Radix Trie, vom compara acest bitcode cu cel de la rădăcină, care în acest moment este nul, deci vom compara 00000000 cu 01000001. Diferența cade în poziția 2 (aici, deoarece x = 1, comparăm bit cu bit în loc de o pereche).

Pentru a crea nodul trebuie să direcționăm copilul din stânga și cel din dreapta către succesorii lor respectivi. Având în vedere că acest nod este rădăcina, prin definiție, copilul său din stânga indică spre el însuși, în timp ce copilul său din dreapta indică spre null. Acesta va fi singurul pointer nul din întreaga trie. Ținând cont de faptul că rădăcina este singurul nod fără părinte. Valoarea, în exemplul nostru vor fi numere întregi imitând o aplicație de numărare a cuvintelor , este setată la 1. Rezultatul acestei operații de inserție este prezentat în figura 8.
În continuare vom insera caracterul B cu codul de bit 01000010. Primul lucru este să verificăm dacă acest caracter se află deja în structură. Pentru a face acest lucru îl vom căuta. Căutarea într-o PATRICIA Trie este simplă (a se vedea pseudocodul din figura 5). După ce se compară cheia rădăcinii cu B, se ajunge la concluzia că sunt diferite, așa că se procedează prin crearea a 2 pointeri: părinte și copil. Inițial, părintele indică rădăcina, iar copilul indică copilul din stânga rădăcinii. În acest caz, ambele indică nodul A. Urmând regula numărul 2, vom itera structura în timp ce inecuația (1) este adevărată.
În acest moment parent.DIFF este egal cu, și nu mai mic decât child.DIFF. Acest lucru încalcă inecuația (1). Deoarece child.VALUE este diferit de null (egal cu 1), comparăm caracterele. Cum A este diferit de B, înseamnă că B nu se află în trie și trebuie inserat.
Pentru a insera începem, din nou, să definim părinte și copil ca înainte, adică părinte indică rădăcina și copil indică nodul stâng al acesteia. Iterația prin structură trebuie să urmeze inecuațiile (1) și (2). Continuăm prin calcularea diff, care este diferența, pe biți, dintre B și child.KEY, care în această etapă este egală cu A (diferența dintre codurile de biți 01000001 și 01000010). Diferența cade pe bitul de la poziția 7 , deci diff = 7.

În acest moment, părinte și copil indică același nod (către nodul A, rădăcina). Deoarece inecuația (1) este deja falsă și child.DIFF este mai mică decât diff, vom crea nodul B și vom îndrepta parent.LEFT către acesta. La fel cum am făcut cu nodul A, trebuie să direcționăm copiii B ai nodului B undeva. Bitul de la poziția 7 din B este 1, astfel încât copilul drept al nodului B va fi îndreptat către el însuși. Copilul stâng al nodului B va fi îndreptat către părinte, în acest caz către rădăcină. Rezultatul final este prezentat în figura 9.
Prin orientarea copilului stâng al nodului B către părintele său, activăm divizarea menționată în regula numărul 2. Atunci când inserăm un caracter al cărui dif se încadrează între 2 și 7, acest pointer ne va trimite înapoi la poziția corectă din care se inserează noul caracter. Acest lucru se va întâmpla atunci când introducem caracterul D.
Dar înainte de aceasta trebuie să introducem caracterul C cu un cod binar egal cu 01000011. Pointerul părinte va indica nodul A (rădăcina). De data aceasta, spre deosebire de momentul în care căutam caracterul B, copilul indică spre nodul B (în acel moment ambii pointeri indicau spre rădăcină).
În acest moment, inecuația (1) este valabilă (parent.DIFF este mai mică decât child.DIFF), așa că actualizăm ambii pointeri, stabilind părinte la copil și copil la copilul din dreapta nodului B, deoarece la poziția 7 bitul lui C este 1.
După actualizare, ambii pointeri indică spre nodul B, încălcând inecuația (1). La fel ca înainte, comparăm codul de biți child.KEY cu codul de biți al lui C (01000010 cu 01000011), concluzionând că acestea diferă la poziția 8. Deoarece la poziția 7 bitul lui C este 1, acest nou nod (nodul C) va fi copilul din dreapta al lui B. La poziția 8 bitul lui C este 1, ceea ce ne face să stabilim copilul din dreapta al nodului C la el însuși, în timp ce copilul din stânga acestuia indică părintele, nodul B în acest moment. Tria rezultată este în figura 10.

Următorul caracter este D (cod bit 01000100). Așa cum am făcut la inserarea caracterului C, vom seta inițial pointerul părinte la nodul A și pointerul copil la nodul B. Inecuația (1) este valabilă, deci actualizăm pointerii. Acum părintele indică nodul B, iar copilul indică copilul din stânga nodului B, deoarece la poziția 7, bitul D este 0. Spre deosebire de inserarea caracterului C, acum copilul indică din nou nodul A, încălcând inecuația (1). Calculăm din nou diferența dintre codurile de biți A și D. Acum, diferența este 6. Din nou, setăm părintele și copilul, așa cum facem în mod normal. Acum, în timp ce inecuația (1) este valabilă, inecuația (2) nu este. Aceasta implică faptul că vom introduce D ca fiind copilul stâng al lui A. Dar cum rămâne cu copiii lui D? La poziția 6, bitul lui D este 1, astfel încât copilul său din dreapta indică spre el însuși. Partea interesantă este că copilul stâng al nodului D va arăta acum spre nodul B, ajungând la tria desenată în figura 11.

Urmează caracterul E cu codul de bit 01000101. Funcția de căutare va returna nodul D. Diferența dintre caracterele D și E se încadrează pe bitul de la poziția 8. Deoarece la poziția 6 bitul lui E este 1, acesta va fi poziționat în dreapta lui D. Structura trie este ilustrată în figura 12.

Ceea ce este interesant la inserarea caracterului F este că locul său este între caracterele D și E, deoarece diferența dintre D și F se află la poziția 7. Dar la poziția 7 bitul lui E este 0, deci nodul E va fi copilul din stânga nodului F. Structura este acum ilustrată în figura 13.

Și, în cele din urmă, inserăm caracterul G. După toate calculele, ajungem la concluzia că noul nod ar trebui plasat ca copil drept al nodului F cu diferența egală cu 8. Rezultatul final este în figura 14.

Până acum am inserat șiruri compuse dintr-un singur caracter. Ce s-ar întâmpla dacă am încerca să inserăm șirurile AB și BA? Cititorul interesat poate lua această propunere ca pe un exercițiu. Două indicii: ambele șiruri diferă de nodul B la poziția 9; iar tria finală este ilustrată în figura 15.

Gândindu-ne la ultima figură, se poate pune următoarea întrebare: Pentru a găsi, de exemplu, șirul BA este nevoie de 5 comparații de biți, în timp ce pentru a calcula codul hash al acestui șir sunt necesare doar două iterații, deci când devine competitivă PATRICIA Trie? Imaginați-vă că inserăm în această structură șirul ABBABABABBBBABABABBA (preluat din exemplul din lucrarea originală PATRICIA din 1968), care are 16 caractere? Acest șir ar fi plasat ca și copil stâng al nodului AB, cu dif la poziția 17. Pentru a-l găsi, am avea nevoie de 5 comparații de biți, în timp ce pentru a calcula codul hash ar fi nevoie de 16 iterații, una pentru fiecare caracter, acesta fiind motivul pentru care Trie PATRICIA este atât de competitiv în căutarea șirurilor lungi.
PATRICIA Trie vs Hash Map
În această ultimă secțiune voi compara Hash Map și PATRICIA Trie în două aplicații. Prima este o numărătoare de cuvinte pe leipzig1m.txt care conține 1 milion de propoziții aleatorii, iar a doua este popularea unui tabel de simboluri cu peste 2,3 milioane de URL-uri din proiectul DMOZ (închis în 2017) descărcate de aici.
Codul pe care l-am dezvoltat și folosit atât pentru a implementa pseudocodul de mai sus, cât și pentru a compara performanța PATRICIA Trie cu Hash Table poate fi găsit pe GitHub-ul meu.
Aceste comparații au fost rulate în boxa mea Ubuntu 18.04. Configurația poate fi găsită în figura 16
.