V mikrokosmech, ve kterých se pohybuji, není datová struktura trie příliš populární. Toto prostředí tvoří především datoví vědci a v menším počtu softwaroví inženýři, kteří pracují se zpracováním přirozeného jazyka (NLP).
Nedávno jsem se ocitl v zajímavé diskusi o tom, kdy použít trie nebo hashovací tabulku. Ačkoli v této diskusi nebylo nic nového, o čem bych zde mohl informovat, stejně jako o výhodách a nevýhodách každé z těchto dvou datových struktur (pokud trochu zagooglujete, najdete mnoho odkazů, které se jimi zabývají), nové pro mě bylo, že existuje speciální typ trie zvaný Patricia Trie a že v některých scénářích tato datová struktura vykazuje srovnatelný výkon jak v čase zpracování, tak v prostoru s hashovací tabulkou, přičemž úlohy jako výpis řetězců se společným prefixem řeší bez dalších nákladů.
S tímto vědomím jsem hledal příběh nebo blog, který by mi pomohl jednoduchým způsobem (eufemismus pro lenost) pochopit, jak algoritmus PATRICIA funguje, speciálně sloužící jako zkratka k přečtení 21stránkového článku publikovaného v roce 1968. Bohužel jsem v tomto hledání neuspěl, takže mi nezbyla žádná alternativa k jeho přečtení.
Mým cílem je tímto příběhem zaplnit výše uvedenou mezeru, tj. mít k dispozici příběh popisující laicky řečeno daný algoritmus.
Abych dosáhl svého cíle, nejprve a stručně představím, pro ty, kteří se nevyznají v pokusech, tuto datovou strukturu. Po tomto úvodu uvedu nejoblíbenější tria, která existují, což mi umožní implementovat a podrobně popsat, jak tria PATRICIA fungují a proč mají tak dobré výsledky. Na závěr tohoto povídání porovnám výsledky (výkon a spotřebu místa) ve dvou různých aplikacích: první z nich je počet slov (<Slovo, frekvence> tria) založený na poměrně rozsáhlém textu; a druhou je sestavení <URL, IP> tria založeného na seznamu více než 2 milionů URL, který spočívá v základním prvku DNS serveru. Obě aplikace byly sestaveny na základě Hash Map a Patricia Trie.
Jak definují Sedgewick a Wayne z Princetonské univerzity ve své knize Algorithms – Fourth Edition (vydavatel: Addison-Wesley) trie neboli prefixový strom je „datová struktura sestavená ze znaků vyhledávacího klíče, která slouží jako vodítko pro vyhledávání“. Tato „datová struktura se skládá z uzlů, které obsahují odkazy, jež jsou buď nulové, nebo odkazují na jiné uzly. Na každý uzel ukazuje právě jeden jiný uzel, který se nazývá jeho rodič (s výjimkou jednoho uzlu, kořene, na který neukazují žádné uzly), a každý uzel má S odkazů, kde S je velikost abecedy (nebo znakové sady)“.
Následující obrázek 1 podle výše uvedené definice obsahuje příklad trie.

Kořenový uzel nemá žádný popisek. Má tři potomky: uzly s klíčem ‚a‘, ‚h‘ a ‚s‘. V pravém dolním rohu obrázku je tabulka se seznamem všech klíčů s jejich příslušnou hodnotou. Z kořene můžeme přejít na ‚a‘ -> ‚i‘ -> ‚r‘. Tato posloupnost tvoří slovo „air“ s hodnotou (například počet výskytů tohoto slova v textu) 4 (hodnoty jsou uvnitř zeleného rámečku). Podle konvence má existující slovo v tabulce symbolů nenulovou hodnotu. Ačkoli tedy slovo „airway“ v angličtině existuje, v této trojici není, protože podle konvence je hodnota uzlu s klíčem „y“ nulová.
Slovo „air“ je zároveň předponou pro slova: „airplane“; a „airways“. Posloupnost ‚h‘ -> ‚a‘ tvoří prefix slov „has“ a „hat“, stejně jako posloupnost ‚h‘ -> ‚o‘ tvoří prefix slov „house“ a „horse“.
Kromě toho, že dobře slouží jako datová struktura řekněme slovníku, slouží také jako důležitý prvek kompletační aplikace. Systém by mohl po zadání slova „air“ uživatelem navrhnout slova „air“ a „airways“ procházením podstromu, jehož kořenem je uzel s klíčem „r“. Další výhodou této struktury je, že lze získat uspořádaný seznam existujících klíčů, a to bez dalších nákladů, procházením tria v orientaci in-order, skládáním dětí uzlu a jejich procházením zleva doprava.
Na obrázku 2 je ukázka anatomie uzlu.

Zajímavé na této anatomii je, že ukazatele na děti jsou obvykle uloženy v poli. Pokud reprezentujeme znakovou sadu S například Extended ASCII, potřebujeme, aby pole mělo velikost 256 znaků. Máme-li znak potomka, můžeme k jeho ukazateli v rodiči přistupovat v čase O(1). Uvážíme-li, že velikost slovníku je N a že velikost nejdelšího slova je M, je hloubka tria také M a procházení struktury trvá O(MN). Uvážíme-li, že obvykle je N mnohem větší než M (počet slov v korpusu je mnohem větší než velikost nejdelšího slova), můžeme O(MN) považovat za lineární. V praxi je toto pole řídké, tj. většina uzlů má mnohem méně dětí než S. Navíc průměrná velikost slov je také menší než M, takže v praxi trvá v průměru O(logₛ N) vyhledání klíče a O(N logₛ N) projití celé struktury.
U této datové struktury existují dva hlavní problémy. Jedním z nich je spotřeba místa. Na každé úrovni L, počínaje nulou, je asimptoticky Sᴸ ukazatelů. Jestliže u Extended ASCII, tj. 256 znaků, je to v omezených paměťových zařízeních problém, situace se zhoršuje, pokud uvažujeme všechny znaky Unicode (je jich 65 000). Druhým je množství uzlů s jedním dítětem, které zhoršuje vstupní a vyhledávací výkon. V příkladu na obrázku 1 mají pouze kořen, klíč „h“ na úrovni 1, klíče „a“ a „o“ na úrovni 2 a klíč „r“ na úrovni 3 více než jednoho potomka. Jinými slovy, pouze 5 uzlů z 27 má dva nebo více potomků. Alternativy k této struktuře řeší především tyto problémy.
Před popisem alternativy (PATRICIA Trie) odpovím na následující otázku: Proč alternativy, když můžeme místo pole použít hašovací tabulku? Hašovací tabulka skutečně pomáhá šetřit paměť s malým snížením výkonu, ale problém neřeší. Čím výše se v trie nacházíte (blíže k nulové úrovni), tím je pravděpodobnější, že bude třeba řešit téměř všechny znaky v libovolné znakové sadě. Dobře implementované hashovací tabulky, jako je ta v Javě (rozhodně patří mezi nejlepší, pravděpodobně nejlepší), začínají s výchozí velikostí a automaticky mění velikost podle prahové hodnoty. V Javě je výchozí velikost 16 s prahem 0,75 a při každé z těchto operací se její velikost zdvojnásobí. Vezmeme-li v úvahu Extended ASCII, v okamžiku, kdy počet dětí v jednom uzlu dosáhne 192, bude velikost hašovací tabulky změněna na 512, i když jich nakonec bude potřeba jen 256.
Radix Trie
Jelikož je PATRICIA Trie speciálním případem Radix Trie, začnu s ní. Ve Wikipedii je Radix Trie definován jako „datová struktura, která představuje prostorově optimalizovanou trie… v níž je každý uzel, který je jediným potomkem, sloučen se svým rodičem… Na rozdíl od běžných stromů (kde se porovnávají celé klíče hromadně od jejich počátku až do bodu nerovnosti) se klíč v každém uzlu porovnává po částech, přičemž množství bitů v této části v daném uzlu je radix r radixové trie“. Tato definice bude dávat větší smysl, když si tuto trojici ukážeme na obrázku 3.
Počet dětí r uzlu v radixové trie je určen následujícím vzorcem, kde x je počet bitů potřebných k porovnání výše uvedeného chunk-of-bitu:

Výše uvedený vzorec stanovuje počet dětí v radixové trie tak, aby byl vždy násobkem 2. Například pro 4-Radix Trie platí x = 2. To znamená, že bychom museli porovnávat kousky dvou bitů, dvojici bitů, protože těmito dvěma bity reprezentujeme všechna desetinná čísla od 0 do 3, celkem tedy 4 různá čísla, pro každé dítě jedno.
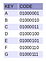
Pro lepší pochopení výše uvedených definic uvažujme příklad na obrázku 3. V tomto příkladu máme hypotetickou sadu znaků, která se skládá z 5 znaků (NULL, A, B, C a D). Rozhodl jsem se je reprezentovat pouze pomocí 4 bitů (mějte na paměti, že to nemá nic společného s r, k reprezentaci 5 znaků stačí 3 bity, ale má to co do činění se snadností nakreslení příkladu). V levém horním rohu obrázku je tabulka mapující jednotlivé znaky na jejich bitovou reprezentaci:
Chci-li vložit znak ‚A‘, porovnám ho bitově s NULL. V pravém horním rohu obrázku 3, v rámečku označeném 1 ve žlutém kosočtverci, vidíme, že se tyto dva znaky liší u první dvojice. Tato první dvojice je ve čtyřbitové reprezentaci znaku A znázorněna červeně. DIFF tedy obsahuje bitovou pozici, kde končí odlišná dvojice.
Pro vložení znaku ‚B‘ jej musíme bitově porovnat se znakem ‚A‘. Toto porovnání se nachází v kosočtverci označeném číslem 2. Rozdíl tentokrát připadá na druhou dvojici bitů, červeně označenou, která končí na pozici 4. Protože druhá dvojice je 01, vytvoříme uzel s klíčem B a nasměrujeme na něj adresu 01 v uzlu A. Toto propojení je vidět ve spodní části obrázku 3. Stejný postup platí pro vložení znaků ‚C‘ a ‚D‘.

V uvedeném příkladu vidíme, že první pár (01 modře) je prefixem všech vložených znaků.
Tento příklad slouží k popisu porovnávání kusů bitů, optimalizaci prostoru (v tomto případě pouze čtyři děti, bez ohledu na velikost znakové sady) a slučování rodičů a dětí (v uzlech dětí jsou uloženy pouze bity, které se liší od kořene), které jsou zmíněny ve výše uvedené definici Radix Trie. Nicméně stále existuje jeden odkaz směřující do nulového uzlu. Řídkost je přímo úměrná r a hloubce trie.
PATRICIA Trie
PATRICIA (Practical Algorithm to Retrieve Information Coded in Alphanumeric, Journal of the ACM, 15(4):514-534, říjen 1968) . Ano, PATRICIA je zkratka!
PATRICIA Trie je zde definována třemi pravidly:
- Každý uzel (TWIN je původní termín PATRICIA) má dvě děti (r = 2 a x = 1 v termínech Radix Trie);
- Uzel se rozdělí na prefix (L-PHRASE v termínech PATRICIA) se dvěma dětmi (každé dítě tvoří BRANCH, což je původní termín PATRICIA) pouze tehdy, pokud dvě slova (PROPER OCCURRENCE v termínech PATRICIA) mají stejný prefix; a
- Každé slovo končící v uzlu bude reprezentováno hodnotou odlišnou od nuly (značka END v původním názvosloví PATRICIA)
Výše uvedené pravidlo číslo 2 znamená, že délka prefixu na každé úrovni je větší než délka prefixu z předchozí úrovně. To bude velmi důležité v algoritmech, které podporují operace PATRICIA, jako je vložení prvku nebo nalezení jiného.
Z výše uvedených pravidel lze definovat uzel podle následujícího obrázku. Každý uzel má jednoho rodiče, kromě kořene, a dva potomky, hodnotu (libovolného typu) a proměnnou diff označující pozici, na které se rozdělení nachází v bitovém kódu klíče

Pro použití algoritmu PATRICIA potřebujeme funkci, která při zadání 2 řetězců vrátí pozici prvního bitu zleva doprava, kde se liší. Již jsme viděli, že to funguje pro radix trie.
Pro práci s triem pomocí PATRICIA, tj. pro vkládání nebo hledání klíčů v něm, potřebujeme 2 ukazatele. Jeden je parent, který inicializujeme tak, že jej nasměrujeme na kořenový uzel. Druhým je child, inicializovaný tak, že jej ukážeme na levého potomka kořene.
Na co bude následovat, bude proměnná diff držet pozici, ve které se vkládaný klíč liší od klíče child.key. Podle pravidla číslo 2 definujeme následující 2 nerovnice:

Nechť nalezený ukazuje na uzel, kde hledání klíče končí. Pokud se found.key liší od vkládaného řetězce, vypočítá se diff pomocí funkce ComputeDiff z tohoto řetězce a found.key. Pokud se rovnají, klíč ve struktuře existuje a jako v každé tabulce symbolů by měla být vrácena hodnota. Při operacích bude použita pomocná metoda BitAtPosition, která získá bit na určité pozici (0 nebo 1).
Pro vyhledávání musíme definovat funkci Search(key). Její pseudokód je na obrázku 4.

Druhou funkcí, kterou budeme v tomto příběhu používat, je funkce Insert(key). Její pseudokód je na obrázku 6.

Ve výše uvedeném pseudokódu se nachází metoda pro vytvoření uzlu s názvem CreateNode. Její argumenty lze pochopit z obrázku 4.
Pro ukázku toho, jak funguje PATRICIA Trie, raději provedu čtenáře operací krok za krokem, aby dokončil vložení 7 znaků („A“, „B“, „C“, „D“, „E“, „F“ a „G“, jak je uvedeno na obrázku 7 vedle) v jejich přirozeném pořadí. Na konci snad pochopíme, jak tato datová struktura funguje.
Znak A se vkládá jako první. Jeho bitový kód je 01000001. Stejně jako u Radix Trie budeme tento bitový kód porovnávat s bitovým kódem v kořeni, který je v tuto chvíli nulový, takže porovnáme 00000000 s 01000001. Rozdíl připadá na pozici 2 (zde, protože x = 1, porovnáváme bit po bitu místo dvojice).

Pro vytvoření uzlu musíme ukázat levého a pravého potomka na jejich příslušné následníky. Protože tento uzel je kořenový, z definice jeho levý potomek ukazuje sám na sebe, zatímco jeho pravý potomek ukazuje na nulu. To bude jediný nulový ukazatel v celé trie. Nezapomeňte, že kořen je jediný uzel, který nemá žádného rodiče. Hodnota, v našem příkladu to budou celá čísla napodobující aplikaci počítání slov , je nastavena na 1. Výsledek této operace vložení je znázorněn na obrázku 8.
Dále vložíme znak B s bitovým kódem 01000010. Nejprve je třeba zkontrolovat, zda se tento znak již ve struktuře nachází. Za tímto účelem jej vyhledáme. Vyhledávání v Trie PATRICIA je jednoduché (viz pseudokód na obrázku 5). Po porovnání klíče kořene s klíčem B dojdeme k závěru, že se liší, takže postupujeme tak, že vytvoříme 2 ukazatele: rodiče a potomka. Zpočátku rodič ukazuje na kořen a potomek na levého potomka kořene. V tomto případě oba ukazují na uzel A. Podle pravidla číslo 2 budeme iterovat strukturu, dokud platí nerovnice (1).
V tuto chvíli se parent.DIFF rovná a není menší než child.DIFF. Tím porušujeme nerovnici (1). Protože hodnota child.VALUE je jiná než null (rovná se 1), porovnáme znaky. Protože A je jiné než B, znamená to, že B není v trie a je třeba ho vložit.
Pro vložení začneme opět definovat rodiče a potomka jako dříve, tj. rodič ukazuje na kořen a potomek na jeho levý uzel. Iterace strukturou musí probíhat podle nerovnic (1) a (2). Pokračujeme výpočtem diff, což je bitový rozdíl mezi B a child.KEY, který je v této fázi roven A (rozdíl bitových kódů 01000001 a 01000010) . Rozdíl připadá na bit na pozici 7 , takže diff = 7.

V tuto chvíli ukazuje rodič i potomek na stejný uzel (na uzel A, kořen). Protože nerovnice (1) je již nepravdivá a child.DIFF je menší než diff, vytvoříme uzel B a ukážeme na něj parent.LEFT. Stejně jako jsme to udělali s uzlem A, musíme někam ukázat na děti uzlu B. Bit na pozici 7 v uzlu B je 1, takže pravý potomek uzlu B bude ukazovat sám na sebe. Levý potomek uzlu B bude ukazovat na rodiče, v tomto případě na kořen. Konečný výsledek je znázorněn na obrázku 9.
Ukázáním levého potomka uzlu B na jeho rodiče umožníme rozdělení uvedené v pravidle číslo 2. Když vložíme znak, jehož rozdíl spadá mezi 2 a 7, tento ukazatel nás pošle zpět na správnou pozici, ze které se vkládá nový znak. To se stane, když vložíme znak D.
Předtím však musíme vložit znak C s bitovým kódem rovným 01000011. Ukazatel parent bude ukazovat na uzel A (kořen). Tentokrát, jinak než když jsme hledali znak B, ukazuje child na uzel B (tehdy oba ukazatele ukazovaly na kořen).
V tuto chvíli platí nerovnice (1) (parent.DIFF je menší než child.DIFF), takže aktualizujeme oba ukazatele, nastavíme parent na child a child na uzel B pravého dítěte, protože na pozici 7 je bit C 1.
Po aktualizaci ukazují oba ukazatele na uzel B, čímž porušujeme nerovnici (1). Stejně jako předtím porovnáme bitový kód child.KEY s bitovým kódem C (01000010 s 01000011) a dojdeme k závěru, že se na pozici 8 liší. Protože na pozici 7 je bit C 1, bude tento nový uzel (uzel C) pravým potomkem uzlu B. Na pozici 8 je bit C 1, díky čemuž nastavíme pravého potomka uzlu C na sebe sama, zatímco jeho levý potomek v tomto okamžiku ukazuje na rodiče, uzel B. Výsledná trojice je na obrázku 10.

Dalším znakem je D (bitový kód 01000100). Stejně jako při vkládání znaku C nastavíme zpočátku ukazatel parent na uzel A a ukazatel child na uzel B. Platí nerovnice (1), takže aktualizujeme ukazatele. Nyní rodič ukazuje na uzel B a dítě ukazuje na levého potomka uzlu B, protože na pozici 7 je bit D 0. Jinak než při vložení znaku C nyní dítě ukazuje zpět na uzel A, čímž se porušuje nerovnice (1). Opět vypočítáme rozdíl mezi bitovými kódy A a D. Nyní je rozdíl 6. Opět nastavíme rodiče a potomka jako obvykle. Zatímco nerovnice (1) platí, nerovnice (2) neplatí. To znamená, že vložíme D jako levého potomka A. Ale co děti D? Na pozici 6 má D bit 1, takže jeho pravé dítě ukazuje samo na sebe. Zajímavé je, že levý potomek uzlu D bude nyní ukazovat na uzel B, čímž dosáhneme tria nakresleného na obrázku 11.

Následuje znak E s bitovým kódem 01000101. Funkce Search vrátí uzel D. Rozdíl mezi znaky D a E připadá na bit na pozici 8. Protože na pozici 6 je bit E 1, bude umístěn napravo od D. Struktura tria je znázorněna na obrázku 12.

Zajímavostí vložení znaku F je to, že jeho místo je mezi znaky D a E, protože rozdíl mezi D a F je na pozici 7. Vložení znaku E do tria se provede na pozici 7. Ale na pozici 7 je bit E 0, takže uzel E bude levým potomkem uzlu F. Struktura je nyní znázorněna na obrázku 13.

A nakonec vložíme znak G. Po všech výpočtech dojdeme k závěru, že nový uzel by měl být umístěn jako pravý potomek uzlu F s rozdílem rovným 8. Konečný výsledek je na obrázku 14.

Dosud jsme vkládali řetězce složené pouze z jednoho znaku. Co by se stalo, kdybychom se pokusili vložit řetězce AB a BA? Zájemce může tuto větu pojmout jako cvičení. Dvě nápovědy: oba řetězce se liší od uzlu B na pozici 9; a výsledná trojice je znázorněna na obrázku 15.

Přemýšlením nad posledním obrázkem lze položit následující otázku: K nalezení například řetězce BA je třeba 5 bitových porovnání, zatímco k výpočtu hashovacího kódu tohoto řetězce stačí pouze dvě iterace, kdy se tedy PATRICIA Trie stává konkurenceschopnou? Představme si, že do této struktury vložíme řetězec ABBABABBBBABABBA (převzatý z příkladu v původním článku PATRICIA z roku 1968), který má 16 znaků? Tento řetězec by byl umístěn jako levý potomek uzlu AB s rozdílem na pozici 17. K jeho nalezení bychom potřebovali 5 bitových porovnání, zatímco výpočet hashovacího kódu by zabral 16 iterací, jednu pro každý znak, což je důvod, proč jsou Trie PATRICIA tak konkurenceschopné při vyhledávání dlouhých řetězců.
PATRICIA Trie vs Hash Map
V této poslední části porovnám Hash Map a Trie PATRICIA ve dvou aplikacích. První je počítání slov na souboru leipzig1m.txt obsahujícím 1 milion náhodných vět a druhou je vyplňování tabulky symbolů s více než 2,3 miliony URL adres z projektu DMOZ (uzavřeného v roce 2017) staženého odsud.
Kód, který jsem vyvinul a použil jak k implementaci výše uvedeného pseudokódu, tak k porovnání výkonu PATRICIA Trie s Hash Table, naleznete na mém GitHubu.
Tato porovnání byla spuštěna v mém boxu Ubuntu 18.04. Konfiguraci naleznete na obrázku 16
.