Dans les microcosmes dans lesquels je suis intégré, les goûts de la structure de données trie n’est pas si populaire. Cet environnement est composé principalement de data scientists et, en plus petit nombre, d’ingénieurs logiciels, travaillant avec le traitement du langage naturel (NLP).
Récemment, je me suis retrouvé dans une discussion intéressante sur le moment où il faut utiliser trie ou table de hachage. Bien qu’il n’y ait rien de nouveau dans cette discussion que je puisse rapporter ici, comme les avantages et les inconvénients de chacune de ces deux structures de données (si vous googlez un peu, vous trouverez de nombreux liens les abordant), ce qui était nouveau pour moi était un type spécial de trie appelé Patricia Trie et, que dans certains scénarios, cette structure de données fonctionne de manière comparable à la fois en temps de traitement et en espace avec la table de hachage, tout en abordant des tâches telles que la liste des chaînes de caractères avec un préfixe commun sans coût supplémentaire.
Avec cela en tête, j’ai cherché une histoire ou un blog pour m’aider à comprendre de manière simple (euphémisme pour la paresse) comment fonctionne l’algorithme PATRICIA, servant spécialement de raccourci pour lire le papier de 21 pages publié en 1968. Malheureusement, je n’ai pas réussi dans cette recherche, me laissant sans alternative pour le lire.
Mon objectif avec cette histoire est de combler la lacune ci-dessus, c’est-à-dire, d’avoir une histoire décrivant en termes profanes l’algorithme à portée de main.
Pour atteindre mon objectif, d’abord, et brièvement, je vais introduire, pour ceux qui ne sont pas familiers avec les essais, cette structure de données. Après cette introduction, je vais énumérer les trie les plus populaires qui existent, ce qui me permettra d’implémenter et de décrire en détail le fonctionnement des trie PATRICIA et pourquoi ils sont si performants. Je terminerai cette histoire en comparant les résultats (performances et consommation d’espace) dans deux applications différentes : la première est un comptage de mots (tuples <WORD, FREQUENCY>) basé sur un texte assez volumineux ; et la seconde construit un tuples <URL, IP>, basé sur une liste de plus de 2 millions d’URL, qui consiste en l’élément central d’un serveur DNS. Les deux applications ont été construites sur la base de Hash Map et de Patricia Trie.
Comme défini par Sedgewick et Wayne de l’Université de Princeton dans leur livre Algorithms – Fourth Edition (éditeur : Addison-Wesley) un trie, ou arbre de préfixe, est « une structure de données construite à partir des caractères de la clé de recherche pour guider la recherche ». Cette « structure de données est composée de nœuds qui contiennent des liens qui sont soit nuls, soit des références à d’autres nœuds. Chaque nœud est pointé par un seul autre nœud, qui est appelé son parent (à l’exception d’un nœud, la racine, qui n’a aucun nœud pointant vers lui), et chaque nœud a S liens, où S est la taille de l’alphabet (ou charset) ».
La figure 1 ci-dessous, suivant la définition ci-dessus, contient un exemple de trie.

Le nœud racine n’a pas d’étiquette. Il a trois enfants : des nœuds avec la clé ‘a’, ‘h’ et ‘s’. Dans le coin inférieur droit de la figure se trouve un tableau listant toutes les clés avec leur valeur respective. À partir de la racine, nous pouvons nous déplacer vers ‘a’ -> ‘i’ -> ‘r’. Cette séquence forme le mot « air » avec une valeur (par exemple le nombre de fois où ce mot apparaît dans un texte) de 4 (les valeurs sont à l’intérieur d’une boîte verte). Par convention, un mot existant dans une table de symboles a une valeur non nulle. Ainsi, bien que le mot « airway » existe en anglais, il n’est pas dans cette trie, car, suivant la convention, la valeur du nœud avec la clé « y » est nulle.
Le mot « air » est également le préfixe des mots : « avion » ; et « voies aériennes ». La séquence ‘h’ -> ‘a’ forme le préfixe de « a » et « chapeau » comme la séquence ‘h’ -> ‘o’ forme le préfixe de « maison » et « cheval ».
En plus de bien servir de structure de données pour, disons, un dictionnaire, il sert aussi d’élément important d’une application de complétion. Un système pourrait proposer les mots « airplane » et « airways » après qu’un utilisateur ait tapé le mot « air », en parcourant le sous-arbre dont la racine est le nœud avec la clé « r ». Un avantage supplémentaire de cette structure est que vous pouvez obtenir une liste ordonnée des clés existantes, sans coût supplémentaire, en parcourant le trie dans une orientation ordonnée, en empilant les enfants d’un nœud et en les parcourant de gauche à droite.
Dans la figure 2, l’anatomie du nœud est illustrée.

Le point intéressant dans cette anatomie est que les pointeurs des enfants sont généralement stockés dans un tableau. Si nous représentons un jeu de caractères S de, par exemple, ASCII étendu, nous avons besoin que le tableau soit de taille 256. En ayant un caractère enfant, nous pouvons accéder à son pointeur dans son parent en O(1) temps. Si l’on considère que la taille du vocabulaire est N et que la taille du mot le plus long est M, la profondeur du trie est également M et il faut O(MN) pour parcourir la structure. Si l’on considère que normalement N est beaucoup plus grand que M (le nombre de mots dans un corpus est beaucoup plus grand que la taille du mot le plus long), on peut considérer que O(MN) est linéaire. En pratique, ce tableau est clairsemé, c’est-à-dire que la majorité des nœuds ont beaucoup moins d’enfants que S. De plus, la taille moyenne des mots est également inférieure à M, donc, en pratique, il faut en moyenne O(logₛ N) pour rechercher une clé et O(N logₛ N) pour parcourir toute la structure.
Il y a deux problèmes principaux avec cette structure de données. Le premier est la consommation d’espace. A chaque niveau L, en commençant par zéro, il y a, assimilé, Sᴸ pointeurs. Si avec l’ASCII étendu, c’est-à-dire 256 caractères, cela pose un problème dans les dispositifs de mémoire limités, la situation empire si l’on considère tous les caractères Unicode (65 000 d’entre eux). Le deuxième problème est la quantité de nœuds avec un seul enfant, ce qui dégrade les performances de saisie et de recherche. Dans l’exemple de la figure 1, seules la racine, la clé « h » au niveau 1, les clés « a » et « o » au niveau 2 et la clé « r » au niveau 3 ont plus d’un enfant. En d’autres termes, seuls 5 nœuds sur les 27 ont deux enfants ou plus. Les alternatives à cette structure traitent principalement ces problèmes.
Avant de décrire l’alternative (PATRICIA Trie), je répondrai à la question suivante : pourquoi des alternatives si nous pouvons utiliser une table de hachage au lieu d’un tableau ? La table de hachage permet vraiment d’économiser de la mémoire avec une faible dégradation des performances, mais ne résout pas le problème. Plus vous êtes haut dans le tableau (proche du niveau zéro), plus il est probable que presque tous les caractères de n’importe quel jeu de caractères devront être traités. Les tables de hachage bien implémentées, comme celle de Java (certainement parmi les meilleures, voire la meilleure), commencent avec une taille par défaut et se redimensionnent automatiquement en fonction d’un seuil. En Java, la taille par défaut est de 16 avec un seuil de 0,75 et elle double sa taille à chacune de ces opérations. En considérant l’ASCII étendu, au moment où le nombre d’enfants dans un nœud atteint 192, la table de hachage sera redimensionnée à 512, même si elle n’a besoin que de 256 à la fin.
Trie Radix
Comme la Trie PATRICIA est un cas particulier de la Trie Radix, je vais commencer par cette dernière. Dans Wikipedia, un Radix Trie est défini comme « une structure de données qui représente un trie optimisé en termes d’espace… dans lequel chaque nœud qui est le seul enfant est fusionné avec son parent… Contrairement aux arbres réguliers (où des clés entières sont comparées en masse depuis leur début jusqu’au point d’inégalité), la clé à chaque nœud est comparée morceau de bits par morceau de bits, où la quantité de bits dans ce morceau à ce nœud est le radix r du radix trie ». Cette définition aura plus de sens lorsque nous exemplifierons cette trie dans la figure 3.
Le nombre d’enfants r d’un nœud dans un trie radix est déterminé par la formule suivante où x est le nombre de bits requis pour comparer le chunk-of-bits mentionné ci-dessus :

La formule ci-dessus établit le nombre d’enfants dans un trie radix comme étant toujours un multiple de 2. Par exemple, pour une Trie Radix 4, x = 2. Cela signifie que nous aurions à comparer des morceaux de deux bits, une paire de bits, car avec ces deux bits nous représentons tous les nombres décimaux de 0 à 3, totalisant 4 nombres différents, un pour chaque enfant.
Pour mieux comprendre les définitions ci-dessus, considérons l’exemple de la figure 3. Dans cet exemple, nous avons un jeu de caractères hypothétique composé de 5 caractères (NULL, A, B, C et D). J’ai choisi de les représenter en utilisant seulement 4 bits (gardez à l’esprit que cela n’a rien à voir avec r, on a seulement besoin de 3 bits pour représenter 5 caractères, mais cela a à voir avec la facilité de dessiner l’exemple). Dans le coin supérieur gauche de la figure, il y a un tableau faisant correspondre chaque caractère à sa représentation binaire.
Pour insérer le caractère ‘A’, je vais le comparer bit à bit avec le NULL. Dans le coin supérieur droit de la figure 3, à l’intérieur de la boîte étiquetée avec 1 dans un diamant jaune, nous pouvons voir que ces deux caractères diffèrent à la première paire. Cette première paire est représentée en rouge dans la représentation à 4 bits de A. Donc DIFF contient la position du bit où la paire différente se termine.
Pour insérer le caractère ‘B’, nous devons le comparer bit à bit avec le caractère ‘A’. Cette comparaison se trouve dans la case diamant étiquetée avec 2. La différence tombe cette fois sur la deuxième paire de bits, en rouge, qui se termine à la position 4. Comme la deuxième paire est 01, nous créons un nœud avec la clé B et nous lui indiquons l’adresse 01 du nœud A. Ce lien est visible dans la partie inférieure de l’écran. Ce lien est visible dans la partie inférieure de la figure 3. La même procédure s’applique pour insérer les caractères ‘C’ et ‘D’.

Dans l’exemple ci-dessus, nous voyons que la première paire (01 en bleu) est le préfixe de tous les caractères insérés.
Cet exemple sert à décrire la comparaison de chunk-of-bits, l’optimisation de l’espace (seulement quatre enfants dans ce cas, quelle que soit la taille du jeu de caractères) et la fusion parent/enfant (stocké aux nœuds enfants uniquement les bits qui diffèrent de la racine) mentionnés dans la définition de Radix Trie ci-dessus. Néanmoins, il y a toujours un lien pointant vers un nœud nul. La parcimonie est directement proportionnelle à r et à la profondeur du trie.
PATRICIA Trie
PATRICIA (Practical Algorithm to Retrieve Information Coded in Alphanumeric, Journal of the ACM, 15(4):514-534, October 1968) . Oui, PATRICIA est un acronyme !
PATRICIA Trie est ici défini par trois règles :
- Chaque nœud (TWIN est le terme original de PATRICIA) a deux enfants (r = 2 et x = 1 en termes de Radix Trie);
- Un nœud n’est divisé en un préfixe (L-PHRASE en termes de PATRICIA) avec deux enfants (chaque enfant formant une BRANCHE qui est le terme original de PATRICIA) que si deux mots (PROPER OCCURRENCE en termes de PATRICIA) partagent le même préfixe ; et
- Chaque mot se terminant sera représenté par une valeur au sein du nœud différente de null (marque END dans la nomenclature originale de PATRICIA)
La règle numéro 2 ci-dessus implique que la longueur du préfixe à chaque niveau est supérieure à la longueur du préfixe du niveau précédent. Ceci sera très important dans les algorithmes qui supportent les opérations PATRICIA comme insérer un élément ou en trouver un autre.
À partir des règles ci-dessus, on peut définir le nœud comme illustré ci-dessous. Chaque noeud a un parent, à l’exception de la racine, et deux enfants, une valeur (de n’importe quel type) et une variable diff indiquant la position où se trouve la scission dans le code binaire clé

Pour utiliser l’algorithme PATRICIA, nous avons besoin d’une fonction qui, étant donné 2 chaînes de caractères, renvoie la position du premier bit, de gauche à droite, où elles diffèrent. Nous avons déjà vu que cela fonctionne pour Radix Trie.
Pour faire fonctionner le trie en utilisant PATRICIA, c’est-à-dire pour y insérer ou trouver des clés, nous avons besoin de 2 pointeurs. Le premier est parent, initialisé en le pointant sur le nœud racine. Le second est child, initialisé en le pointant sur l’enfant gauche de la racine.
Sur ce qui suit, la variable diff tiendra la position où la clé insérée diffère de child.key. En suivant la règle numéro 2, nous définissons les 2 inéquations suivantes :

Let found pointe vers le nœud où la recherche d’une clé se termine. Si found.key est différent de la chaîne en cours d’insertion, diff sera calculé, via une fonction ComputeDiff, en utilisant cette chaîne et found.key. Si elles sont égales, la clé existe dans la structure et, comme dans toute table de symboles, la valeur doit être retournée. Une méthode d’aide appelée BitAtPosition, qui récupère le bit à une position spécifique (0 ou 1), sera utilisée lors des opérations.
Pour effectuer une recherche, nous devons définir une fonction Search(key). Son pseudocode est dans la figure 4.

La deuxième fonction que nous utiliserons dans cette histoire est la fonction Insert(key). Son pseudocode est dans la figure 6.

Dans le pseudocode ci-dessus, il y a une méthode pour créer un nœud appelé CreateNode. Ses arguments peuvent être compris à partir de la figure 4.
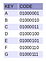
Pour illustrer le fonctionnement d’un Trie PATRICIA, je préfère guider le lecteur dans une opération étape par étape pour compléter l’insertion de 7 caractères (‘A’, ‘B’, ‘C’, ‘D’, ‘E’, ‘F’ et ‘G’ comme spécifié dans la figure 7 ci-contre) dans leur ordre naturel. A la fin, avec un peu de chance, on aura compris comment fonctionne cette structure de données.
Le caractère A est le premier à être inséré. Son code binaire est 01000001. Comme pour Radix Trie, on va comparer ce bitcode avec celui de la racine qui à ce moment est nul, donc on compare 00000000 avec 01000001. La différence tombe à la position 2 (ici comme x = 1 nous comparons bit par bit au lieu d’une paire d’entre eux).

Pour créer le nœud nous devons pointer les enfants gauche et droit vers leurs successeurs respectifs. Comme ce noeud est la racine, par définition, son enfant gauche pointe vers lui-même tandis que son enfant droit pointe vers null. Ce sera le seul pointeur null de toute la triade. Rappelons que la racine est le seul nœud sans parent. La valeur, dans notre exemple sera des entiers imitant une application de comptage de mots, est fixée à 1. Le résultat de cette opération d’insertion est montré dans la figure 8.
Puis nous allons insérer le caractère B avec le bitcode 01000010. La première chose à faire est de vérifier si ce caractère est déjà dans la structure. Pour ce faire, nous allons le rechercher. La recherche dans un Trie PATRICIA est simple (voir le pseudocode de la figure 5). Après avoir comparé la clé de la racine avec celle de B, on conclut qu’elles sont différentes. On procède donc en créant 2 pointeurs : parent et child. Initialement, parent pointe vers la racine et child pointe vers l’enfant gauche de la racine. Dans ce cas, les deux pointent vers le noeud A. En suivant la règle numéro 2, nous allons itérer la structure pendant que l’inéquation (1) est vraie.
À ce moment, parent.DIFF est égal à, et non inférieur à, child.DIFF. Cela rompt l’inéquation (1). Comme child.VALUE est différent de null (égal à 1), nous comparons les caractères. Comme A est différent de B, cela signifie que B n’est pas dans le trie et doit être inséré.
Pour insérer, nous commençons, à nouveau, à définir parent et enfant comme précédemment, c’est-à-dire que parent pointe sur la racine et enfant pointe sur son nœud gauche. L’itération à travers la structure doit suivre les inéquations (1) et (2). Nous continuons en calculant diff, qui est la différence, bit par bit, entre B et child.KEY, qui à ce stade est égal à A (différence entre les codes binaires 01000001 et 01000010) . La différence tombe sur le bit en position 7 , donc diff = 7.

À ce moment, parent et enfant pointent vers le même nœud (vers le nœud A, la racine). Comme l’inéquation (1) est déjà fausse et que child.DIFF est inférieur à diff, nous allons créer le noeud B et pointer parent.LEFT vers lui. Comme nous l’avons fait avec le noeud A, nous devons pointer les enfants B du noeud vers quelque part. Le bit en position 7 dans B est 1, donc l’enfant droit du noeud B pointera vers lui-même. L’enfant gauche du noeud B pointera vers le parent, la racine dans ce cas. Le résultat final est montré dans la figure 9.
En pointant l’enfant B gauche du nœud vers son parent, nous activons le split mentionné dans la règle numéro 2. Lorsque nous insérons un caractère dont le diff tombe entre 2 et 7 ce pointeur nous renverra à la position correcte à partir de laquelle on insère le nouveau caractère. Cela se produira lorsque nous insérons le caractère D.
Mais avant cela, nous devons insérer le caractère C dont le bitcode est égal à 01000011. Le pointeur parent pointera vers le nœud A (la racine). Cette fois, différemment de quand nous cherchions le caractère B, child pointe vers le nœud B (à ce moment-là, les deux pointeurs pointaient vers la racine).
À ce moment, l’inéquation (1) tient (parent.DIFF est inférieur à child.DIFF) donc nous mettons à jour les deux pointeurs, mettant parent à child et child à B right child du nœud parce qu’à la position 7 le bit de C est 1.
Après la mise à jour, les deux pointeurs pointent vers le nœud B, brisant l’inéquation (1). Comme nous l’avons fait auparavant, nous comparons le code binaire child.KEY avec le code binaire de C (01000010 avec 01000011) en concluant qu’ils diffèrent à la position 8. Comme à la position 7, le bit de C est 1, ce nouveau nœud (nœud C) sera l’enfant droit de B. À la position 8, le bit de C est 1, ce qui nous permet de définir l’enfant droit du nœud C comme étant lui-même, tandis que son enfant gauche pointe vers le parent, le nœud B à ce moment. Le trie résultant est dans la figure 10.

Le prochain caractère est D (code binaire 01000100). Comme nous l’avons fait pour l’insertion du caractère C, nous allons définir initialement le pointeur parent sur le nœud A et le pointeur enfant sur le nœud B. L’inéquation (1) est valide donc nous mettons à jour les pointeurs. Maintenant, le parent pointe vers le nœud B et l’enfant pointe vers l’enfant gauche du nœud B, car à la position 7, le bit de D est 0. Contrairement à l’insertion du caractère C, l’enfant pointe maintenant vers le nœud A, ce qui rompt l’inéquation (1). Nous calculons à nouveau la différence entre les codes binaires A et D. La différence est maintenant de 6. La différence est maintenant de 6. Nous définissons à nouveau le parent et l’enfant comme nous le faisons normalement. Maintenant, alors que l’inéquation (1) est valide, l’inéquation (2) ne l’est pas. Cela implique que nous allons insérer D comme enfant gauche de A. Mais qu’en est-il des enfants de D ? A la position 6, le bit de D est 1, donc son enfant droit pointe vers lui-même. La partie intéressante est que l’enfant gauche du nœud D pointera maintenant vers le nœud B atteignant le trie dessiné dans la figure 11.

Le prochain est le caractère E avec le code binaire 01000101. La fonction de recherche renvoie le nœud D. La différence entre les caractères D et E tombe sur le bit en position 8. Comme à la position 6 le bit de E est 1, il sera positionné à droite de D. La structure de la trie est illustrée dans la figure 12.

L’intérêt d’insérer le caractère F est que sa place est entre les caractères D et E, car la différence entre D et F est en position 7. Mais à la position 7, le bit de E est 0, donc le nœud E sera l’enfant gauche du nœud F. La structure est maintenant illustrée dans la figure 13.

Et, enfin, nous insérons le caractère G. Après tous les calculs, nous concluons que le nouveau nœud doit être placé comme enfant droit du nœud F avec diff égal à 8. Le résultat final est dans la figure 14.

Jusqu’à présent nous insérons des chaînes de caractères composées d’un seul caractère. Que se passerait-il si nous essayions d’insérer les chaînes AB et BA ? Le lecteur intéressé peut prendre cette proposition comme un exercice. Deux indices : les deux chaînes diffèrent du nœud B en position 9 ; et le trie final est illustré dans la figure 15.

En réfléchissant à la dernière figure, on peut se poser la question suivante : Pour trouver, par exemple, la chaîne BA on a besoin de 5 comparaisons de bits, tandis que pour calculer le code de hachage de cette chaîne seulement deux itérations sont nécessaires, alors quand est-ce que le Trie PATRICIA devient compétitif ? Imaginez que nous insérions dans cette structure la chaîne ABBABABBBBABABBA (tirée de l’exemple de l’article original de PATRICIA datant de 1968) qui compte 16 caractères ? Cette chaîne serait placée en tant qu’enfant gauche du nœud AB avec diff en position 17. Pour la trouver, nous aurions besoin de 5 comparaisons de bits, tandis que pour calculer le code de hachage, il faudrait 16 itérations, une pour chaque caractère, ceci étant la raison pour laquelle les Trie PATRICIA sont si compétitifs lors de la recherche de longues chaînes.
Trie PATRICIA vs Hash Map
Dans cette dernière section, je vais comparer Hash Map et Trie PATRICIA dans deux applications. La première est un comptage de mots sur leipzig1m.txt contenant 1 million de phrases aléatoires et la seconde consiste à peupler une table de symboles avec plus de 2,3 millions d’URL du projet DMOZ (fermé en 2017) téléchargé ici.
Le code que j’ai développé et utilisé à la fois pour mettre en œuvre le pseudocode ci-dessus et comparer les performances de PATRICIA Trie avec la table de hachage peut être trouvé sur mon GitHub.
Ces comparaisons ont été exécutées dans ma boîte Ubuntu 18.04. Configurantion peut être trouvée dans la figure 16
.